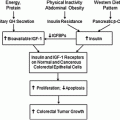
Fig. 8.1
An example of MA-plots for one microarray sample with the raw (left) and normalized (right) expression values. Red lines show LOWESS smoothing curves, blue lines correspond to zero log-fold change in expression. The log-fold changes between gene expressions in the sample and median array (vertical axis M) are not centered around zero for the raw data. Also, raw data show more pronounced curvature (an undesired feature in an MA-plot) than normalized data
Samples with outlier expression may be a concern, because outlying samples might influence (bias) a normalization procedure in an undesirable way. Thus, it might be advisable to remove these outlying samples and re-normalize the data without them. However, caution should be exercised when removing outliers, as they might represent interesting biological outliers and not technical artifacts.
Particular attention should be paid to the gene expression data generated using archival formalin fixed paraffin embedded (FFPE) samples. Nucleic acids extracted from archived FFPE samples are typically degraded, their overall quality is significantly poorer than that of the frozen tissues and corresponding gene expression data are much noisier [42]. However, microarray techniques have developed that can partially mitigate this degradation and provide valid mRNA profiling data within FFPE materials [43]. Samples that fail to produce data of a reasonable quality must be identified and excluded from the analysis (prior to normalization, to avoid biases). It might be useful to inspect distributional properties of the samples as a function of the FFPE block age.
After preprocessing, proper summarization at the gene or transcript level and, if necessary, removing outlying observations, a data matrix is obtained. Typically, rows represent genes and columns represent samples. This matrix is ready for downstream analysis and hypothesis testing.
8.3.2 Differential Expression Analysis
One of the most basic questions that can be addressed using microarray and RNA-Seq data is ‘what genes are differentially expressed between phenotypes or conditions of the experiment.’ When comparing mean expression values between two experimental conditions, such as comparing tumor and normal tissue, or short and long term survival, statistical procedures include simple two-sample or paired t-tests of each individual gene or transcript, provided that distributional assumptions are met. Log-transformed normalized gene expression values from microarray experiments usually do not display critical departures from normality, but if in a particular experiment they do, nonparametric tests, such as Mann–Whitney or Wilcoxon tests could replace t-tests. For study designs with multiple experimental conditions and/or additional categorical and continuous covariates a linear models approach is taken. Most familiar are simple and multiple linear regressions, Analysis of variance (ANOVA), and Analysis of covariance (ANCOVA), which belong to the family of linear models. Other commonly used models are logistic regression to analyze binary outcomes or Cox proportional hazards regression used for analysis of time-to-event data.
The most commonly used tool for fitting linear models for gene expression analysis is a Bioconductor package called limma [44]. Functions of the package use an empirical Bayes approach and compute moderated t-statistics. In moderated t-statistics, sample variances for each gene are shrunk toward the pooled estimate of variance. This approach provides robust inference even for the smaller sample sizes [45].
Distributional properties of the microarray and RNA-Seq data are fundamentally different. As mentioned above, microarray-based gene expression values, that are summarized from the intensities of multiple probes that comprise a probeset, and typically log-transformed, usually approximately meet normality conditions. RNA-Seq data is different, in that the expression of the transcript is represented by read counts, and is described best by a negative binomial distribution, therefore it is inappropriate to apply a linear models pipeline developed for microarrays directly.
Recent additions to the limma package allow for analysis of the RNA-Seq data. Using a transformation algorithm called voom [46] the counts are transformed using a robust LOWESS (locally weighted scatterplot smoothing) regression that estimates the mean-variance relation and transforms the log-counts scaled to the library size for linear modeling using the limma pipeline.
The Bioconductor package DeSeq2 takes a direct approach and models observed raw read counts as a negative binomial distribution with mean equal to a value proportional to the concentration of the cDNA fragments from that gene, in a sample scaled by a normalization factor to account for different sequencing depth, GC-content, gene length, etc. [47]. That value proportional to the concentration of the cDNA fragments is further modeled using a generalized linear models approach with a design matrix describing experimental conditions. An empirical Bayes approach is used for shrinkage of the count’s variances.
8.3.3 Correcting for Multiple Testing
When comparing groups for differentially expressed genes several thousands of statistical tests are performed at a time, some of which are found to be statistically significant just by chance due a to a type I error—incorrect rejection of the true null hypothesis. Multiple testing correction is applied to avoid high numbers of false positive results. One approach is to control for the family-wise error rate (FWER; probability of making one or more type I errors) by multiplying the p-values by the total number of tests, known as the Bonferroni correction. In practice, a Bonferroni correction is usually too conservative, as it drastically reduces the size of the test, and therefore leads to an unaffordable loss of power, leading to type II errors—failing to reject the null hypothesis when the alternative is true. Less conservative modifications of the Bonferroni correction to control for FWER are also available, for example Holm’s step-wise procedure. Another adopted alternative to controlling FWER is controlling False Discovery Rate (FDR). FDR is an expected proportion of errors among the rejected hypothesis [48], and is less conservative than controlling FWER while providing a good control for multiple testing. Several procedures have been proposed to calculate FDR, such a Benjamini and Hochberg [48], Benjamini and Yekutieli [49], q-value [50], empirical Bayes [51], etc. Most bioinformatics software reports both p-values and FDR.
8.3.4 Principal Components Analysis
Principal components analysis (PCA) is an unsupervised statistical technique that identifies uncorrelated (orthogonal) directions of the largest variability in the data by finding an appropriate rotation. It is usually used to obtain a lower dimensional representation of the high-dimensional data. Modifications of PCA for sparse data and supervised versions have also been proposed. While there is no guarantee that the component representing the largest variability found by PCA will be associated with the variables of biological interest, in practice for well-designed experiments with a strong signal that defines the phenotypes in the gene expression data, PCA works well and can be useful for data visualization.
However, sometimes the largest variability in the data will be associated with known technical variables, such as batches. In this case these unwanted effects could be removed by regressing out principal components associated with nonbiological variability. This approach is widely used in genome-wide association studies to adjust genotypes for individual’s ancestry [52].
Another useful PCA application is summarizing expression activity of a pathway with a reduced number of observations (as compared to representing a pathway by a vector of expression values of all genes that belong to the pathway) or even by a single number [53]. The principal components directions are calculated using the expression values of the genes that belong to the pathway of interest, and projection of the original data onto first several principal components directions is then used for further analysis. The number of directions to use is usually decided based on the percent of total variation explained by each component.
8.3.5 Gene Sets (Pathway) Analysis
Gene sets, or pathways analysis (GSA) is one of the easiest and most popular ways to interpret a list of genes resulting from differential gene expression or similar type of analysis in terms of biological concepts. GSA allows to determine whether a list of genes share features like participating in the same biological processes or metabolic pathway, are a target of a common transcription factor, or belong to the same functional module. It is not uncommon that similarly designed studies report nonintersecting lists of ‘top’ genes. This could be due to differences in the assays that were used to obtain expression data, differences in power of the studies, and other sources of variability that are beyond control. Results obtained at the gene sets level tend to be more stable across the studies. Additionally, each gene might not contribute enough to the difference between the phenotypes to be detected at the individual level, but moderate changes across many genes that belong to the same pathway might.
There are several computational methods to perform gene sets analysis, each answering a slightly different scientific question [54]. For the purposes of this section, by gene sets and pathways we will mean collections of the genes assigned to non-exclusive groups according to some annotation. While there exist sophisticated methods that take into account directional relationships between the genes, here we describe basic methods that do not take those relationships into account. The choice of gene set collections for a particular analysis is entirely dictated by the scientific question one is trying to answer, and it is common to consider several collections. The Broad Institute, for example, maintains a database of curated gene sets that are organized into several collections that is called the Molecular Signatures Database (MSigDb; [55]).
GSA methods can be divided into two classes: “cut-off” (or overrepresentation) and “non cut-off” based. Cut-off methods take a list of genes, usually resulting from filtering of a ranked list of differentially expressed genes, and tests whether the genes that belong to a gene set are overrepresented in that list. Hypergeometric or Fisher’s exact tests are usually used to test the null hypothesis that observing the genes from the gene set in a predefined list of a given size happened by chance, i.e., if the list was selected from a universe of all genes at random. The cut-off methods are subjective, in a sense that if one chooses a different threshold for selecting genes the resulting significantly overrepresented genes sets or pathways could be different. However, these methods are still useful when the ranking for all genes is not available, or when the gene list of interest was not obtained directly from the differential gene expression analysis, but was selected in some other way, for example by a variable selection procedure that optimizes discrimination between two phenotypes in a multivariate model.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree