Scientific Basis of Cancer Chemotherapy

Michael C. Perry

Carl E. Freter

Until recently the majority of chemotherapeutic agents in use today were developed empirically. Knowledge of the regulation of growth in mammalian cells expanded enormously, which led to a greater understanding of how many chemotherapy drugs work and has changed the face of drug development. This chapter is not meant to be a comprehensive review on the mechanism of action of every chemotherapeutic agent, but rather it addresses the nature of the problem of drug therapy for cancer, provides a framework for understanding how chemotherapy drugs act, and highlights the broad range of present and future targets of chemotherapy drugs.

SEARCHING FOR THE BIOCHEMICAL BULLET

At the beginning of the 20th century, Paul Ehrlich observed that certain histologic stains were selectively concentrated in microorganisms and reasoned that such specificity might be used therapeutically if substances that were toxic to bacteria could be found. He coined the term chemotherapy during his search for a chemical that would cure syphilis. Thus began the search for magic bullets against disease, a search that met with only limited success until the fortuitous discovery of penicillin, which launched an era of specific bacterial therapy. For many years, no anticancer agents were found that even approached the specificity of the agents used against bacteria.

The development of presently available chemotherapeutic drugs that are active against cancer cells has been, with rare exceptions, the result of empiricism, luck, or trial and error. Targeted agents are the welcome exception to this rule. The discovery of nitrogen mustard during chemical warfare research is the well-reported first example, but even at that time, hydroxyurea had been on the shelf for more than half a century with its activity undiscovered.¹ In later years, agents that were discarded as excessively toxic were to prove a fertile source of anticancer drugs. The origin of the idea of the antifols is unclear or even disputed.²

The first clearly successful designer drug for cancer was Heidelberger’s 5-fluorouracil (5-FU).³ Phenylalanine mustard, designed for melanoma because phenylalanine is the precursor of melanin, was ineffective in that tumor in spite of the indisputable biochemical logic of its construction. Over the years, numerous anticancer agents have been discovered, most by accident and a few by design, and a variety of metabolic inhibitors have been developed.

The metabolism of the cancer cell has been thought to be so similar to that of the normal cell that investigators have been forced to use rather minute differences through which drugs might exert a differential effect. Traditionally, the most important such difference has been considered to be the rapid rate of division of the cancer cell relative to most other body tissues. The pioneering work of Skipper demonstrated that even this small difference allowed chemotherapeutic cures in rapidly proliferating animal tumors such as the L1210 mouse leukemia.

SKIPPER’S LAWS

In the late 1970s, Skipper⁴ conducted a series of classic experiments at the Southern Research Institute in Birmingham, Alabama, using the L1210 mouse leukemia that established a set of laws concerning cancer chemotherapy. These laws still apply today, although our understanding of Gompertzian growth has made their application more complex. The L1210 tumor cells are in logarithmic (or exponential) growth; that is, all of the cells are in cycle and dividing, with no cells in a resting phase, and the cell number doubles at a tumor-specific rate. Skipper’s laws apply only to the cells that are proliferating in this way.

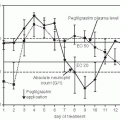
The first of Skipper’s laws is that the doubling time of proliferating cancer cells is a constant, forming a straight line on a semilog plot. Furth and Kahn⁵ had shown in 1937 that a single surviving cell leads to treatment failure. Skipper showed that death results when the malignant cells reach a critical number or fraction of mouse body weight. Thus, survival is a function of the number of tumor cells injected into the mouse (or, by analogy, the tumor body burden in humans at the time of diagnosis).

The second law is that cell kill by drugs follows first-order kinetics; that is, the percentage of cells killed at a given drug dose in a given tumor is a constant, regardless of the body burden of tumor cells. Thus, a drug that kills 99% of tumor cells kills this fraction regardless of the size of the tumor. By convention, one speaks of log kill, the logarithm by which the original cell number must be reduced to equal the remaining cell number (e.g., 99% represents a 2-log kill). From these two simple laws, it is possible to understand mathematically how L1210 mouse leukemia is cured (or not cured). In the model system, it is even possible to calculate cure probabilities that can be confirmed experimentally. This work has had a continuing influence on the conceptual framework that dominates our approach to chemotherapy, as was illustrated by the emphasis on high-dose chemotherapy with stem cell rescue.

Growth Fraction

It may be that the simple Skipper model applies to an occasional human malignancy that is readily curable by
chemotherapy in early stage disease. Trophoblastic neoplasms, testicular germ cell tumors, and Burkitt lymphoma come to mind. Many have even hoped that the micrometastases of some common tumors behave similarly. However, few human cancers are composed of such highly responsive proliferating cells.

In solid tumors in animals and overwhelmingly in humans, Skipper’s laws apply only to the proliferating or stem cell compartment within the tumor, the fraction of cells within the total tumor that is actively growing. In 1960, Mendelsohn⁶ proposed the concept of the growth fraction. He suggested that perhaps tumors had cells equivalent to the stem cells present in normal tissues, a subpopulation of cells whose proliferation accounted for all of the growth of the tumors. Such a population would be the logical target for chemotherapy or radiation therapy. Destruction of the tumor stem cell population, it was argued, might eradicate the tumor as certainly as destruction of the marrow stem cell population terminated hematopoiesis. Using tritiated thymidine, it is possible to determine experimentally the fraction of cells in this proliferating population, but this is not clinically practical. Attempts to modify therapy on the basis of estimates of the growth fraction as determined by various techniques have not been successful.

Gompertzian Growth

The fact that the proliferating cell population is distinct from the nonproliferating population accounts in part for the therapeutic refractoriness of human tumors. Human tumors show a difference from the straight-line growth on a semilog plot seen by Skipper with L1210 mouse leukemia. Instead, human tumors follow a curve called Gompertzian, which describes a population increasing as a result of birth and decreasing as a result of death. Experimentally, tumor cell populations approximate this curve because in addition to proliferating cells, there are subpopulations that have ceased to proliferate and cells that have died.

Tannock⁷ has shown that as cells accumulate into even a small mass, the diffusion process by which oxygen reaches the tumor cells is inadequate to supply cells in the center. Expanding solid tumors regularly outgrow their blood supply, the development of which lags behind the leading edge of invading tumor cells. This leads to anoxia, slowing of the cell cycle, exit of some cells into the G0 nonproliferating phase, and cell death and necrosis. As the cell cycle slows, some cells exit the proliferating pool and become significantly less sensitive to chemotherapy, and Skipper’s laws of cell kill no longer apply. A major rationale for fractionation of radiation therapy has always been that tumor shrinkage allows circulation to improve during therapy, thus causing resting cells to enter the proliferating radiation-sensitive pool.

The Gompertzian growth curve is sigmoid. Cell numbers accumulate slowly at first, because the number of dividing cells is small; then cells accumulate rapidly, reaching a maximum growth rate at approximately one-third of maximum tumor volume. A gradual slowing of the rate of growth follows, almost to a plateau, as the tumor approaches the volume that is necessary to kill the host. Tumor growth has been fit to a variety of model curves, and it is likely that no single equation describes all malignant growth. However, a sigmoid growth curve approximating Gompertzian growth is seen in many of the malignancies studied. Alternative models that challenge Gompertzian growth with temporarily dormant tumor cells have been proposed, and computer modeling of these systems resembles actual survival data.⁸

The dynamics of Gompertzian growth have been emphasized by Norton and Simon.⁹ Small tumors have the largest growth fraction, presumably because their supply of nutrients and oxygen is optimal. Because the total cell number is small, however, even a large growth fraction yields only a small increase in tumor cell number. At the other extreme of the curve, in large tumor masses, total cell number is very large, but the growth fraction is at a minimum, probably because the number of anoxic and necrotic cells has reached a maximum. In the middle portion of the curve, absolute tumor cell growth reaches a maximum because, although neither the total cell number nor the fraction of proliferating cells is at a maximum, their product does reach a maximum (at approximately one-third of maximum tumor volume).

Because Skipper’s laws apply only to the proliferating fraction, it is clear that the best opportunity (from a purely kinetic standpoint) to achieve total cell kill is in the early portion of the curve, when growth fraction is at a maximum. The maximum measurable tumor response is seen at the midportion of the curve, where the growth rate is greatest. This is the best place to estimate drug efficacy against a particular tumor. A comparable kill of proliferating cells at the upper portion of the curve is unlikely to show a measurable response because the growth rate is so small.

Assuming they are not dormant, micrometastases are presumed to have a high growth fraction; thus, from kinetic considerations alone, the chance at total cell kill is highest because fewer cells are in the nonproliferating phase of the cell cycle. Such reasoning led to the enthusiasm for adjuvant chemotherapy, and indeed, success has been encountered in childhood malignancies, breast, colon, and, more recently, lung cancer. These successes are, however, far less than was hoped for and less than theory had led us to believe possible. Why? Perhaps because adequate importance was not given to tumor progression and heterogeneity leading to the development of genetic resistance.

Genetic Resistance

The exact mechanism of resistance to chemotherapy drugs is the subject of Chapter 2. This discussion is limited to genetic and statistical considerations of resistance to chemotherapy. Genetic resistance, unlike kinetic resistance, discussed earlier, is a function of total body tumor burden, not simply the kinetics of a particular metastatic focus, because genetic resistance results from mutations that occur with cell doubling. Because micrometastases are clones from cells that have undergone many prior divisions within the primary tumor, genetic resistance becomes a dominant factor. Large tumors with many generations of tumor cells offer the best potential for the evolution of resistant clones of cells.

Several investigators have emphasized the evolution of human tumors by natural selection of those mutations that predispose to malignant growth.¹⁰^,¹¹^,¹² Essential to such theories is the assumption that tumors have an inherently greater mutation rate than normal cells. Furthermore, with progression, there seems to be a continued increase in mutation rate.¹³ Our understanding of the increased mutation rate in cancer has been greatly augmented by the characterization of cellular mechanisms that ensure the integrity of the genome in normal cells. The tumor suppressor gene p53 is one of the best-characterized genes of this type. In response to various types of DNA damage, p53 protein levels increase, cause a delay in the cell cycle, and allow for DNA repair to take place.¹⁴ When damage to DNA is severe, p53 induces programmed cell death. Exactly how p53 is activated by DNA damage is not entirely known. p53 is inactivated in many tumor cells, and this contributes significantly to a wide variety of additional genetic changes in these cells.

Another class of proteins that normally functions to maintain genomic integrity directly is that involved in mismatch repair. Germ line mutations of mismatch repair genes are responsible for the inherited cancer syndromes Lynch I, Lynch II, and hereditary nonpolyposis colon cancer.¹⁵ Loss of mismatch repair functions in somatic cells has also been demonstrated to occur in sporadic cancers. Because mutation is a random event, the number of drug-resistant clones is a direct function of the number of cell divisions that have occurred in the tumor. Strong evidence has been found that the size of the primary tumor in the best human model studied, breast cancer, is directly related to the incidence of metastasis and survival.¹⁶^,¹⁷

Goldie-Coldman Hypothesis

An important consequence of the development of drug resistance as tumors progress is that at the time of diagnosis most tumors possess resistant clones. Goldie and Coldman¹⁸ have attempted to quantify the role that this might play in cancer therapy. If 1 g of tumor, 10⁹ cells, is the minimum tumor size for detection, and 10^-5 is a probable tumor mutation rate per gene, such a tumor might contain 10⁴ clones that might be resistant to a given drug. (This simple calculation does not take into account a host of potential errors.) We would anticipate encountering drug resistance, therefore, even with small tumors. However, resistance to two drugs would be less likely, assuming that the resistance involves independent mechanisms. Resistance by independent mechanisms should be seen in <1 cell in 10⁵ × 10⁵, or 10¹⁰. This is only one doubly resistant clone per 10 g tumor. Thus, a 3-g primary tumor with micrometastases might have no doubly resistant cells.

DRUG TARGETS IN CANCER: A COMPARATIVE PERSPECTIVE

Comparing drug targets in the treatment of bacterial and viral diseases to the treatment of cancer helps to frame the issue of drug targets in cancer. Bacteria possess numerous enzymes that are either unique to, or sufficiently different from, the host such that we have numerous classes of drugs with wide therapeutic indices. Viral genomes code for a limited number of genes, and they rely heavily on the host to provide basic metabolic functions. Nevertheless, the enzymatic differences in viral genes (e.g., herpes simplex virus thymidine kinase activates acyclovir more readily than mammalian thymidine kinase) or unique viral gene products (reverse transcriptase and protease in the case of HIV) have allowed for the development of active drugs.

In the case of cancer, the situation is much different. For the most part, cancer cells use the same biochemical machinery as normal cells (exceptions are discussed below). Thus, for the majority of cancers, no “optimal” drug target of a vital enzyme is unique to the cancer cell. The biochemical targets of many chemotherapeutic agents are well characterized, but these targets are often identical in normal and cancer cells. For example, vinca alkaloids and taxanes inhibit the function of tubulin, but there are no data to suggest that the tubulin in cancer cells is more susceptible to these agents than the tubulin in normal cells. Moreover, abnormal tubulin function has not been found to play a role in the malignant phenotype. For the purpose of discussion, the term biochemical target is used to refer to the cellular machinery with which a given chemotherapeutic agent interacts directly (and often that biochemical target is identical in normal and cancer cells).

HOW DOES CHEMOTHERAPY WORK IN THE ABSENCE OF AN “OPTIMAL” DRUG TARGET?

Given that many chemotherapy regimens have significant activity against cancers with acceptable toxicity to normal tissues, the question is raised as to how these drugs act if they do not target unique enzymes. To address this question it is helpful to consider the factors that cause cells to become malignant and the concept of programmed cell death or apoptosis.

For a cell to become malignant, it may acquire an increase in the activity of positively acting growth signals (activation of protooncogenes), a decrease in the activity of negatively acting growth signals (loss of tumor suppressor gene function), and a decrease in the activity of some of the pathways leading to programmed cell death. For any given cancer, numerous alterations are required, and specific alterations are necessary to occur in specific types of tumors. Thus, what makes a cancer cell unique is that normal signals that regulate proliferation and cell death are out of balance in such a way as to produce the malignant phenotype. This regulatory imbalance, however, also means that normal mechanisms that protect cells from metabolic and genomic insults are missing in cancer cells, and, thus, the state of dysregulation itself becomes the target of chemotherapy.

Only gold members can continue reading. Log In or Register to continue