Rheology and Vessel Wall Stress

Larry V. Mcintire

Juan M. JiméNez

Suzanne G. Eskin

Peter F. Davies

The classical conditions considered favorable for thrombosis and attributed to the triad of observations assembled by Virchow¹ in 1856 remain central to the modern interpretation of thrombotic mechanisms. They are (a) alterations in normal blood flow, particularly low flow or its cessation; (b) vessel wall injury, particularly of the protective anticoagulant endothelium; and (c) blood hypercoagulability. To promote most forms of pathological coagulation, blood-borne elements are delivered to a relatively fixed interface of the vessel wall surface. This places rheology (study of the flow of materials) and its principal components—molecular transport, shear stresses, and strain deformation of cells—as important physical properties in the regulation of coagulation. In this chapter, we first define and outline in context the fluid mechanical aspects of rheology and the experimental in vitro models that address mechanisms of interactions between blood and surfaces and vascular cells. We then consider how different natural vascular geometries in vivo promote spatial variations of rheology that can influence the phenotype of the endothelium with implications for its anticoagulation properties. Finally, we consider how similar rheologic principles apply at the microscale to flow around intracoronary stents to promote a local environment conducive to stent-related thrombosis.

Blood flow-induced shear stresses and pulsatile-induced vessel wall strain can considerably modulate blood kinetics and vascular cell function. Local mechanical forces can directly alter the metabolism and gene expression of vascular cells.²^,³^,⁴ While the kinetics of thrombus formation depends on local flow conditions, flow-responsive cell receptors and ligands support cell-cell and cell-blood protein adhesion under arterial, venous, and pathologic shear conditions. Additionally, mass transport of cells and proteins to and from reactive surfaces, such as a damaged vessel wall, varies in different flow regimes. Understanding hemodynamics requires the application of the fundamentals of classical fluid mechanics and rheology coupled with deformable vessel mechanics. Theoretical models of the vascular system have been developed by applying the governing principles of fluid flow and mass transport. On the basis of these relatively simple models, dynamic experimental systems have been designed that simulate vascular shear conditions. These systems are valuable tools for investigating the molecular mechanisms supporting vascular processes important to thrombosis under flow, as seen in vivo.

BLOOD FLUID DYNAMICS

Principles of Rheology

Physical blood flow characteristics have long been considered to be as important to vascular function as are the blood vessel itself and the circulating components. A simple, but relevant, model of the vascular system may be developed by considering the steady, pressure-driven laminar flow of an incompressible newtonian fluid through a long cylindrical tube with a constant cross-sectional area.⁵^,⁶^,⁷^,⁸ These conditions yield an axisymmetric flow field that can be described by the radial position (r), the mean fluid velocity (v), and the vessel radius (R):

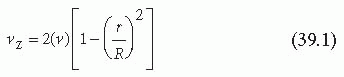
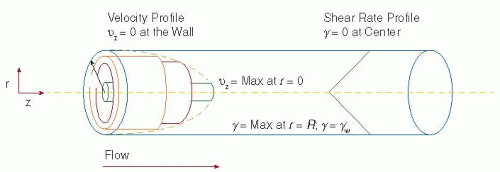
As suggested by Equation 39.1, the axial velocity, v_z, reaches a maximum at the center of the tube where r is equal to zero (see FIGURE 39.1). Moving away from this center position, velocity decreases as the wall of the tube is approached. The fluid is assumed not to slip along the wall; that is, the fluid velocity at the wall is assumed to be zero.⁶ The presence of maximum velocity at the center and zero at the wall yields a velocity gradient called Shear, which refers to the relative motion of the different fluid planes in the velocity profile. The shear rate (γ) is a measure of the velocity gradient and indicates the rate at which fluid layers are sliding past one another.

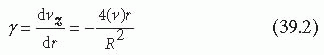
The units of the shear rate are inverse time, commonly reported as inverse seconds. Although the fluid velocity is greatest at the center of the tube, the velocity gradient, and therefore the shear rate, is zero there. Conversely, at the wall of the tube, the velocity gradient and therefore the shear rate reach a maximum (FIGURE 39.1), but the actual velocity is zero. Important to the rheology of the vascular system is the shear rate at the wall of the tube (r = R), which corresponds to the shear rate at the vessel surface (γ_w):

The mean fluid velocity, (v_z), may be expressed in terms of physical quantities as in Equation 39.4:

where Q is the volumetric flow rate. Substituting Equation 39.4 into the wall shear rate equation (Equation 39.3) leads to a more practical expression of γ_w:

FIGURE 39.1 Velocity (v_z) and shear rate (γ) profiles produced by steady, laminar flow of an incompressible, newtonian fluid through a long cylindrical tube with a constant cross-sectional area. Shear refers to the relative motion of the different fluid planes in the velocity profile. The shear rate indicates how fast the fluid layers are sliding past one another. The fluid velocity is greatest at the center of the tube while the shear rate is zero. Conversely, at the wall of the tube, the shear rate (γ_w) reaches a maximum and the fluid velocity is zero. r, radial position; R, vessel radius. (Modified from Alevriadou BR, McIntire LV. Rheology. In: Loscalzo J, Schafer AI, eds. Thrombosis and hemorrhage. Boston, MA: Blackwell, 1994:369-381; Goldsmith HL, Turitto VT. Rheological aspects of thrombosis and haemostasis: basic principles and applications. ICTH9 Report—Subcommittee on Rheology of the International Committee on Thrombosis and Haemostasis. Thromb Haemost 1986;55:415-435.)

As predicted from the range of vessel sizes and volumetric blood flow rates, the wall shear rates corresponding to the different regions of the vascular system can vary greatly (see Table 39.1).

In addition to shear rate, the fluid shear stress is commonly used to describe rheologic conditions in the vascular system. Shear stress is a measure of the force per unit area exerted by the flowing blood as different fluid layers slide past one another. Shear stress is typically expressed in dynes per square centimeter (dyn per cm²) or Pascals (1 Pa = 10 dyn per cm²). For newtonian fluids, shear stress (τ_z) is directly proportional to both the viscosity of the fluid (µ) and the shear rate⁷:

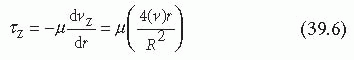
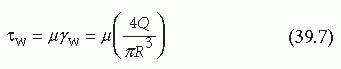
At the vessel wall, r = R, and Equation 39.6 becomes the equation for the wall shear stress (τ_w):

Table 39.1 Shear rates in the vascular system

Vessel	Shear Rate (Per Second)
Large arteries	300-800
Veins	20-200
Arterioles	500-1,600
Stenotic vessels, stents	800-10,000
(Modified from Alevriadou BR, McIntire LV. Rheology. In: Loscalzo J, Schafer AI, eds. Thrombosis and hemorrhage. Boston, MA: Blackwell, 1994:369-381.)

Fluids resist shear, and so pressure gradients along the tube length are necessary to produce the work required to overcome the frictional resistance to flow. In fully developed laminar flow, a balance exists between the force generated by the pressure gradient (acting across the luminal surface) and the force of shear resistance generated by viscous drag (acting on the vessel wall)⁵:

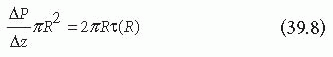
where ΔP is the pressure difference across a given tube length in the axial direction, Δz. Substituting for τ(R), which equals τ_w in Equation 39.7, yields the Hagen-Poiseuille equation that relates the pressure drop along a vessel to the volumetric flow rate⁷:

This model of the vascular system describes flow regimes where viscous forces rather than inertial forces dominate, a type of flow known as Poiseuille flow.⁵^,⁶^,⁷ The Reynolds number (N_Re) is a dimensionless parameter that describes the relative importance of the inertial and viscous forces present under flow⁶:

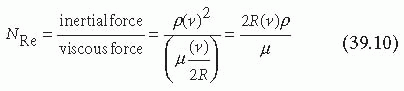
where ρ is the fluid density. When the viscous forces are dominant relative to the inertial forces, specifically when N_Re is less than approximately 2,100, the fluid flow is laminar and Equations 39.1 through 39.9 are valid descriptions of the velocity and shear profiles.⁵^,⁷ This is nearly always the case in the straight portions of blood vessels, with the possible exception of the largest vessels with high blood flow rates, such as the ascending aorta, and in severely stenotic atherosclerotic vessels.

When N_Re is >2,100, the steady, Poiseuille flow becomes unstable and is replaced by complex, turbulent flow regimes.⁵^,⁶^,⁷ Under these conditions, the inertial forces required to accelerate and decelerate the fluid along its flow path dominate. The pulsatile motion of blood flow contributes to the inertial forces present, and a specific modified Reynolds number has been developed to determine when inertial forces resulting from the pulsations in the cardiac cycle must be considered. This dimensionless parameter is called the Womersley alpha parameter⁵:

where ωis the frequency of the oscillation in radians per second. Pulsation effects predominantly impact the flow fields in major arteries that have large diameters and are located proximal to the heart where oscillations have not been significantly dampened by vascular compliance.⁵

Adding to the complexity of flow in the vascular system is the elasticity of the blood vessels. As indicated by Equations 39.5 and 39.9, the shear profiles and the pressure gradients required to produce flow are highly sensitive to changes in the vessel radius. Although most vessels do not substantially dilate under the oscillatory conditions of normal blood flow, very large vessels (e.g., the aortic and the pulmonary arteries) experience radial changes during the different phases of the cardiac cycle.⁵ Additionally, the velocity and shear profiles in a broad distribution of vessels are affected by events such as vasoconstriction and vessel stenosis that also lead to changes in vessel radius.

Applicability to Blood Vessels

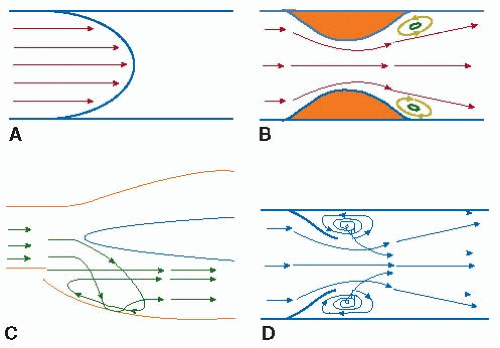
The model of the blood vessel as a long cylindrical tube is applicable to much of the vascular system, and in the straight portions of vessels, turbulence due to a Reynolds number higher than 2,100 is rarely observed. Even in the presence of physiologic shear rates, however, complex vessel geometries may change the flow from simple Poiseuille to a more complex form while remaining laminar. This complexity can induce flow separation from the vessel wall, stagnant regions, transient flow reversal, and eddy formation.⁷^,⁸ In the vascular system, recirculating flow conditions increase the residence time between the vessel wall and circulating cells and proteins, leading to a potential increase in the local deposition of the components necessary for plaque and thrombi formation. FIGURE 39.2 outlines some common sites of vascular flow complexity, which include bifurcations, T-junctions, highly curved vessels (e.g., aortic arch), regions near valves, and vessels with abruptly changing diameters such as a stenosis.⁵^,⁹^,¹⁰^,¹¹^,¹² These sites correspond with areas of increased thrombi and plaque formation.¹³^,¹⁴^,¹⁵^,¹⁶^,¹⁷^,¹⁸^,¹⁹

Nonnewtonian Characteristics

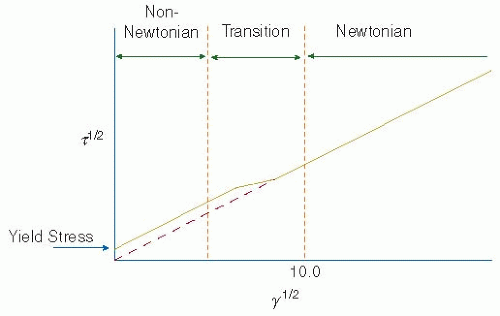
In addition to geometric and flow-rate influences, blood flow regimes vary because the viscosity of blood depends on the shear rate applied; that is, blood is not strictly a newtonian fluid.²⁰ At very low-shear rates, blood does not flow in response to the subthreshold levels of shear stress applied.²⁰^,²¹^,²² This property of having a yield stress is characteristic of elastic materials rather than newtonian fluids. After the yield stress is applied, blood flows and, as the shear rate is increased further, the effective viscosity of blood decreases (see FIGURE 39.3).²⁰^,²³^,²⁴^,²⁵ In contrast to whole blood, plasma is a newtonian fluid.²¹ Therefore, the nonnewtonian properties of blood can be attributed to the presence of cells and cell crowding. All cells in the bloodstream experience shear from the flowing blood. If the cells were simply hard spheres, the shear would cause simple rotation and
translation.²⁶^,²⁷ Owing to the viscoelastic nature of cells, however, shear can twist, stretch, or compress the cells causing deformations.²⁶^,²⁸ Red blood cells, constituting 99% of the blood cellular volume, contribute significantly to the nonnewtonian nature of blood. At low shear rates (<50/s), fibrinogen mediates red cell aggregation into chains called rouleaux.⁵^,²⁰^,²⁹ As the shear rate is increased, the rouleaux breaks down and the effective blood viscosity decreases.²⁵^,³⁰^,³¹ At shear rates >20/s, red cells deform and align in the direction of flow.³²^,³³ Deformations on single cells in dilute suspensions lead to cell migration toward the center of the flow stream³²^,³³ due to the Magnus effect. However, in concentrated suspensions, crowding restricts the rotation and translational movements of the red cells and increases the number of red blood cell collisions. These crowding effects drive the cells toward the wall and offset the migration of deformable particles to the vessel center.³² In vessels with diameters larger than 100 µm, the flow of a suspension with a physiologic concentration of red cells will result in a cell-free layer of approximately 4 µm at the wall.⁵^,³² Red cell crowding and collisions also complicate the flow paths of circulating white blood cells, platelets, and large plasma proteins.³²^,³³ Additionally, under physiologic red cell concentrations, the velocity profile is no longer parabolic as in Poiseuille flow, but becomes blunted at the leading edge.⁵^,³² Despite all these limitations, blood can normally be considered a homogeneous, newtonian fluid for shear rates >100 to 200/s.⁵^,²⁰ At these shear rates, the viscosity of blood remains relatively constant and is determined primarily by the hematocrit, temperature, and the concentration of fibrinogen and other proteins.²⁰

FIGURE 39.2 Streamlines in normal Poiseuille flow (A) and flow at sites of complex laminar flows, including vessels with abruptly changing diameters (B), bifurcations (C), and regions near valves (D). (Modified from Karino T, Goldsmith HL, Motomiya M, et al. Flow patterns in vessels of simple and complex geometries. Ann N Y Acad Sci 1987;516:422-441.)

FIGURE 39.3 The nonnewtonian nature of blood. At very low shear rates (γ), blood will not flow in response to the subthreshold levels of shear stress (τ) applied. After the yield stress is reached, blood will flow, and as the shear rate is increased further, the viscosity of blood will decrease, as indicated by the decrease in slope with increasing shear rate. For newtonian fluids, the shear stress is directly proportional to the shear rate over the entire range of shear rates and no yield stress is present. Blood behaves as a newtonian fluid at shear rates >100 to 200/s. (Modified from Merrill EW. Rheology of blood. Physiol Rev 1969;49:863-888.)

Blood Cell Rolling and Adhesion

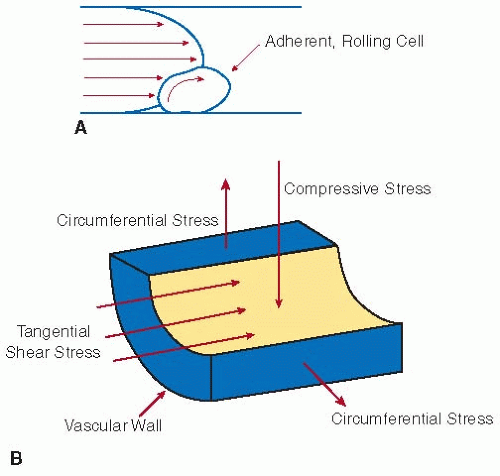
The shear forces due to flowing blood also influence the interactions between the vascular wall and adherent cells. The shear force and torque that a cell experiences when it is tethered to a surface depend on the cell size, the fluid viscosity, and the shear rate.³⁴^,³⁵^,³⁶ At higher shear forces, stronger cell-surface bonds are required to support firm cell adhesion. If the energy from shear in the bloodstream is high enough to deform the cell membrane and overcome the adhesive bond strength, cells will not adhere firmly to the wall.³⁶ Under these conditions, rapid cell-surface bond formation may support transient adhesion, or rolling, on the vascular surface (see FIGURE 39.4A). Cells that constitute the vascular wall itself, such as endothelial cells and smooth muscle cells, also experience tangential shear stress when exposed to flowing blood. Additionally, these cells may experience circumferential stress resulting from deformations caused by expansion and contraction of the blood vessel as well as compressive stress resulting from hydrodynamic pressure (FIGURE 39.4B).³^,⁴

BLOOD TRANSPORT PROCESSES

Diffusion and Convection

The primary function of blood is to transport materials to and from the organs, thereby sustaining life. Although vital, this transport may also augment pathological states such as thrombosis and atherosclerosis. The transport of materials occurs by two processes: diffusion and convection. Diffusion is the movement of material relative to the average fluid motion, irrespective of whether the fluid is flowing or stationary. Diffusion is random and results from Brownian motion of the particles. Convection is the movement of materials with the fluid and results from flow. Diffusion of materials is a very slow process in liquids, whereas convection can be very rapid. If flow is present, convection forces will dominate the mass transfer in blood, and diffusion effects will be negligible in the directions of flow. The Peclet number (N_Pe) is a dimensionless parameter that describes the relative importance of convection and diffusion in a given fluid stream⁷^,³⁷:

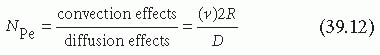
FIGURE 39.4 A: Shear forces acting on an adherent, rolling cell in a flow stream. B: Stresses acting on cells that constitute the vascular wall, such as endothelial cells and smooth muscle cells. Tangential shear stress results from the flow of blood over the vascular wall. Circumferential stress results from deformations caused by the expansion and contraction of the blood vessel, whereas compressive stress results from hydrodynamic pressure. (Modified from Papadaki M, Eskin SG. Effects of fluid shear stress on gene regulation of vascular cells. Biotechnol Prog 1997;13:209-221.)

where D is the molecular diffusion coefficient. Large Peclet numbers correspond to fluid flow where convection dominates, whereas for small Peclet numbers, diffusion is the dominant method of mass transport.

Considering again the model of the vascular system using Poiseuille flow of a newtonian fluid through a cylindrical tube of constant cross-sectional area, convection moves fluid along streamlines parallel to the wall and, therefore, the effects of diffusion are negligible in the axial direction. In the radial direction, convection does not occur and mass transfer is due solely to diffusion. The rate of mass transfer is proportional to the product of the molecular diffusivity and the local concentration gradient. Under these conditions, radial diffusion is required to transport material to the wall, and the steady state mass balance
at any point in the tube for a single species reduces to (neglecting homogeneous reactions):

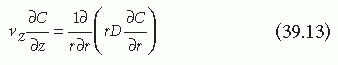
where C is the concentration of the species in the bulk fluid and D is the effective diffusion coefficient.⁸^,³⁸ When turbulence, which generates an effective radial convection that directly pushes cells and soluble proteins to the wall (cf FIGURE 39.2), is present, Equation 39.13 does not apply. Turbulence and complex laminar flows in the vascular system most commonly result from complex vessel geometries or high flow rates, although blood pulsations and vessel elasticity may also contribute to the development of secondary flows. Independent of its origin, any radial transport present greatly enhances the transfer of material from the bloodstream to the wall of the vessel.

Cell and Protein Transport

Mass transfer processes are also significantly affected by the presence of red blood cells, even in steady, laminar flow regimes where blood can be considered newtonian. Because red cells deform in response to shear, the cells align in the direction of flow and migrate to the center of the flow stream. This effect is less pronounced in blood with a normal hematocrit flowing at high shear rates, but even under these physiologic conditions, a thin red cellfree layer exists at the wall. Radial mixing of circulating platelets, white blood cells, and large protein components occurs as these components are pushed to the vessel surface by red cell crowding in the vessel center. Increasing hematocrit increases the frequency of platelet, white cell, and protein collisions with the vessel wall.⁵ Relative to Brownian motion alone, movements by red cells can increase the diffusivity of platelets by two to three orders of magnitude.³⁹ The diffusion of platelets in response to red cells has been quantified and is a function of the shear rate³⁷^,³⁸^,³⁹:

where b is a proportionality constant and n is a power law constant.

On a reactive surface, such as a damaged vessel wall, both fluid dynamics and reaction kinetics influence mass transport. To solve the mass transfer equations, the mass and the momentum boundary layers must first be evaluated.⁵^,⁷ These boundary layers indicate the distance from the wall at which the concentration profile (mass boundary layer) or the velocity profile (momentum boundary layer) reaches maximum values. When the Peclet numbers are large, indicating convection forces are dominant, the height of the mass boundary layer is much smaller than the height of the momentum boundary layer. Under these conditions, it can be assumed that within the mass boundary layer the diffusion coefficient is essentially the diffusion coefficient at the wall and the velocity profile is a linear function of the distance from the wall. Applying these two assumptions, Equation 39.13, developed for steady state, laminar, Poiseuille flow through a cylindrical tube with constant cross-sectional area, can be solved using the following boundary conditions⁵^,⁷:

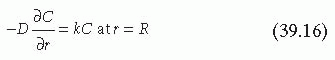
where δ is the thickness of the boundary layer, C_∞ is the concentration of the homogeneous reactant outside the boundary layer, and k is the reaction rate constant. The boundary conditions also assume the reaction is first order and the surface does not become saturated or exhibit decreasing reactivity. Evaluation and substitution of these boundary conditions leads to the general solution for the steady state flux (j) of platelets at any point on the surface⁴^,³⁷:

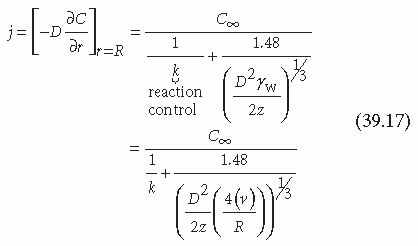
As shown in Equation 39.17, the flux of platelets at any point on the vessel surface is determined by the wall shear rate of the fluid (γ_w), the axial position (z), the reactant concentration in the homogeneous phase outside the boundary layer (C_∞), the reaction rate constant (k), and the effective diffusion coefficient (D).

Platelet Transport

To investigate the thrombotic process, it is useful to determine the parameters controlling platelet transport to the surface under three different vascular conditions. The first condition occurs when platelets flow across an intact monolayer of endothelial cells. In this case, the surface is nonthrombogenic and k « D. Therefore, the flux of platelets at the vessel wall is limited by the reaction kinetics and no longer depends on the axial position or the shear rate:

The second condition occurs when platelets flow across a mildly reactive surface, k [asymptotically equal to] D, and Equation 39.17 cannot be simplified. In this circumstance, in order to determine the flux of platelets at the wall, the equations of motion must be solved first. For simple cases, such as steady Poiseuille flow, these solutions can be found analytically. However, when more complex flow regimes are present, the equations of mass transfer must be determined simultaneously with the equations of motion, and an analytical solution is difficult.⁶^,⁸

The third condition occurs when platelets flow across a very reactive surface (e.g., exposed subendothelium), D « k, and the flux is limited by the diffusion of platelets to the surface⁷^,³⁸:

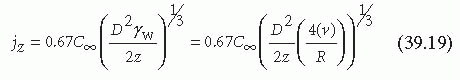
In this case, flux depends on the shear rate, the axial position, and the effective diffusion coefficient. As shown in Equation 39.14, the effective diffusion coefficient of platelets in flowing blood is a function of the shear rate. This indicates that for a given increase in shear rate, platelet flux at the vessel wall will increase by more than γ^1/3_w. The inverse relation between the axial position and the platelet flux is compounded by the depletion of platelets in the mass boundary layer as a result of upstream thrombi growth.⁴⁰ In addition to platelets, circulating proteins and other soluble compounds that support platelet adhesion and growth of thrombi may become depleted in the mass boundary layer. Platelets partially offset the decrease in the delivery of soluble blood components by secreting activating factors and other necessary compounds that then accumulate downstream of the growing thrombi.⁴¹ Despite the presence of these secreted components, the rate of thrombus growth on the thrombogenic components of the subendothelial matrix is decreased in the axial direction.⁴⁰

MODELS OF THROMBOSIS UNDER FLOW

Thrombosis in the vascular system may occur in the bulk fluid phase leading to circulating platelet aggregates or on the vessel wall leading to mural thrombus growth. To identify the molecular mechanisms supporting each type of thrombosis, the dynamic nature of the vascular system must be incorporated into experimental models. This requires the application of engineering principles to develop systems that are physiologically relevant to a number of conditions present in the vascular system.

Aggregometry

The platelet aggregometer was one of the first experimental systems developed to study thrombosis occurring in the bulk fluid phase.⁴² In this system, aggregation in platelet-rich plasma can be monitored over time by measuring light scattering or particle counts. The observed platelet aggregation depends on the addition of chemical agonists to the platelet-rich plasma that induce platelet binding to fibrinogen or von Willebrand factor (vWF).⁴³^,⁴⁴^,⁴⁵^,⁴⁶ Agonists include substances present in the blood, such as adenosine diphosphate (ADP),⁴² but nonphysiologic modulators, such as the antibiotic ristocetin⁴⁷ or the snake venom botrocetin,⁴⁴ also induce aggregation and have been used extensively to study thrombosis. Agitation is required for aggregation to occur, and, therefore, the system can be described as shear dependent. However, the shear produced by the aggregometer is low and cannot be quantified with certainty owing to the variable flow patterns produced in response to agitation.

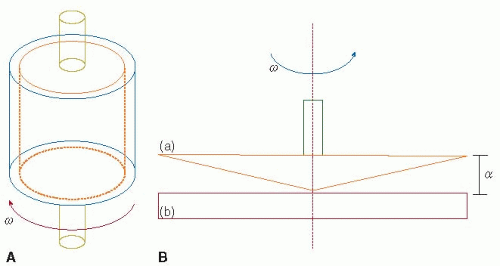FIGURE 39.5 Schematic of a concentric, or Couette, viscometer (A) and cone-and-plate viscometer (B). These rotational viscometers can produce a constant and uniform shear stress on cells and proteins in liquid suspensions, independent of the individual particle location. In a Couette viscometer, samples are placed between a stationary bob and a rotating outer cylindrical shell. In a cone-and-plate viscometer, samples are placed between a rotating cone (a) and a stationary plate (b). The cone angle (α) typically ranges from 0.3 to 1.0 degree. The shear stress that particles experience in a cone-and-plate viscometer depends on the cone angle, the rotation rate (ω), and the fluid viscosity (Equation 39.20). (Modified from Alevriadou BR, McIntire LV. Rheology. In: Loscalzo J, Schafer AI, eds. Thrombosis and hemorrhage. Boston, MA: Blackwell, 1994:369-381; Wang LN, Keller KH. Augmented transport of extracellular solutes in concentrated erythrocyte suspensions in Couette flow. J Colloid Interface Sci 1985;103:210-225.)

Viscometry

In contrast to the aggregometer, rotational viscometers can produce constant and uniform shear stress on all cells and proteins in liquid suspensions, independent of the individual particle location.⁶ The shear profiles in viscometer systems are well characterized and can be varied widely to match a number of physiologic and pathologic vascular conditions. Shear stresses high enough to directly induce platelet aggregation can be developed in viscometer systems, so that the addition of chemical agonists is not necessary.⁴⁸^,⁴⁹^,⁵⁰^,⁵¹^,⁵² In concentric, or Couette, viscometers, the sample to be investigated is placed between a stationary bob and a rotating outer cylindrical shell (see FIGURE 39.5A). In cone-and-plate viscometers, the sample of interest is placed between a rotating cone and a stationary platen (FIGURE 39.5B). To study arterial thrombosis, the rotating cone and stationary platen are separated by approximately 25 µm, and the cone angle ranges from 0.3 to 1.0 degree. Over the range of shear stresses used to investigate arterial thrombosis, blood viscosity is constant and
the shear stress is varied by changing the shear rate. The shear rate in a cone-and-plate viscometer depends on the cone angle (a) and the rotation rate of the cone (ω):

The extent of shear-induced platelet aggregation can be determined by directly comparing the number of single platelets in samples before and after exposure to shear.⁵²^,⁵³^,⁵⁴ Additionally, the size of the platelet aggregates formed in response to shear can be quantified.⁵⁵^,⁵⁶

Platelet aggregation in the bulk fluid phase can be investigated in viscometer systems using whole blood, platelet-rich plasma, or washed platelet suspensions. The presence of other cellular and protein components will affect platelet function and, therefore, whole blood is particularly useful for studying samples from patients receiving therapeutics,⁵⁷ recovering from a thrombotic event,⁵⁸ or both. However, the use of washed platelets is extremely valuable to isolate and investigate distinct molecular mechanisms supporting the thrombotic process. For example, by using washed platelet suspensions in physiologic concentrations, it has been shown that shear stress induces the binding of vWF to the platelet glycoprotein (GP) Ib and GP IIb/IIIa receptors.⁵⁹ More recently, using dilute suspensions of washed platelets, it has been determined that vWF binding to platelet GP Ib precedes binding to platelet GP IIb/IIIa.⁶⁰ The cone-and-plate viscometer system can also be used to study cell-surface interactions by immobilizing cells or proteins on the stationary plate. This method has been used to study the responses of smooth muscle cells and endothelial cells to shear including quantifying the released compounds and changes in gene expression.⁶¹^,⁶²^,⁶³^,⁶⁴^,⁶⁵^,⁶⁶^,⁶⁷^,¹⁵²

Flow Chambers

Cell-surface interactions have also been investigated through the use of flow chambers. In these systems, whole blood or a cell suspension is perfused through the chamber across a surface of immobilized cells or proteins. Parallel plate,⁶⁸^,⁶⁹^,⁷⁰^,⁷¹ annular,⁷²^,⁷³^,⁷⁴^,⁷⁵^,⁷⁶ and tubular⁶⁵^,⁷⁷^,⁷⁸^,⁷⁹^,⁸⁰ flow chamber geometries have been developed. The parallel plate flow chamber, consisting of a polycarbonate slab, a silicon gasket, and a glass coverslip, can be used to illustrate the fundamental principles of these systems (see FIGURE 39.6). The glass coverslip forms the bottom side of the parallel plate flow chamber, and cells or proteins may be immobilized on this surface. The thickness of the silicon gasket determines the height of the gap between the coverslip and the polycarbonate slab. Fluid is pumped across this gap through the chamber. The wall shear stress in the system depends on the height of the gap (G), the width of the chamber (W), the fluid viscosity (µ), and the volumetric flow rate through the chamber (Q)⁶^,⁸⁰:

In the range of shear stresses applied to investigate arterial thrombosis, plane Poiseuille flow is developed and the velocity and shear profiles are similar to those shown in FIGURE 39.1. The use of washed platelets or platelet-rich plasma in flow chambers is limited because the absence of red blood cells considerably changes the mass transfer of platelets to the surface. Therefore, to study platelet-mediated events in arterial thrombosis, whole blood is generally perfused through the chambers across glass coverslips coated with thrombogenic components of the subendothelial matrix, such as collagen or vWF. Significant insight into the molecular mechanisms supporting mural thrombosis, including the roles of fibrinogen and vWF and the platelet receptors GP Ib and GP IIb/IIIa, has been gained through the use of whole blood in flow chambers.⁷⁴^,⁷⁵^,⁷⁶^,⁸¹^,⁸²^,⁸³^,⁸⁴^,⁸⁵^,⁸⁶ Distinct pathways in the thrombotic process are commonly investigated by the addition of blocking antibodies or by the use of patient blood that is deficient in an individual component. Specific interactions may also be studied by using mammalian cells transfected with only the receptor or ligand of interest.⁸⁷^,⁸⁸^,⁸⁹ The transfected cells may be in the fluid suspension, immobilized on the surface, or both. In addition to basic mechanism studies, flow chambers have been used to evaluate the effects of potential or current therapeutic compounds on mural thrombosis from patient samples under arterial shear conditions.⁹⁰^,⁹¹

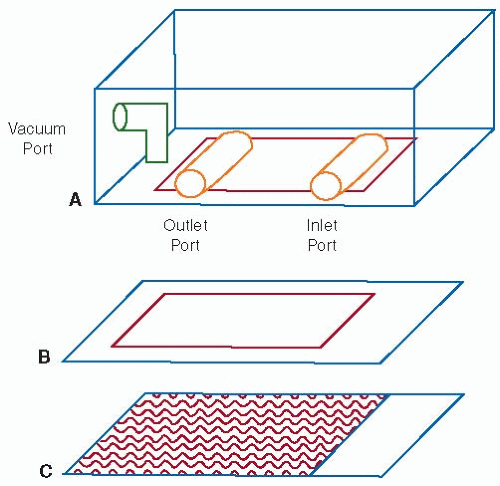FIGURE 39.6 Schematic of a parallel plate flow chamber. The chamber consists of a polycarbonate slab (A), a silicon gasket (B), and a glass coverslip (C) held together by vacuum. The thickness of the silicon gasket determines the height of the gap between the coverslip and the polycarbonate slab. A syringe pump connected to the outlet port draws fluid across this gap through the chamber. The wall shear stress depends on the height of the gap, the width of the chamber, the fluid viscosity, and the flow rate through the chamber (Equation 39.21).

Both arterial and venous shear conditions can be produced using flow chambers of the same geometry, with the only modification required being a change in the volumetric flow rate (Equation 39.21). A wide range of laminar shear conditions have been used to study the interactions of platelets and leukocytes with immobilized proteins, endothelial cells, or transfected
mammalian cells. Turbulent or complex laminar flow regimes, such as those in regions of stenoses or valves, may be produced by changing the geometry of the chamber or tube to resemble the complex geometry of interest. Under these conditions, the equations of Poiseuille flow (Equations 39.1 through 39.10, 39.21) no longer apply.

Measurement of Platelet Deposition by Imaging

Endpoint measurements of platelet deposition after perfusion of whole blood through a flow chamber may be measured either by fixing and staining the mural thrombi formed⁸¹^,⁹²^,⁹³^,⁹⁴^,⁹⁵ or by using radiolabeled platelets reconstituted in blood.¹⁵^,⁹²^,⁹⁴^,⁹⁶^,⁹⁷ Using these methods, the total number of platelets deposited may be evaluated by observing thrombi morphology with light microscopy or by radioactive measurements and imaging. Although these methods provide a snapshot of thrombi growth at a specific point, direct visualization of platelet deposition over time may be determined by combining epifluorescent microscopy and digital image processing.⁶⁸^,⁷¹^,⁸⁶^,⁹⁸^,⁹⁹^,¹⁰⁰ In this method, platelets are fluorescently labeled before perfusion through the flow chamber. Platelets can be labeled by adding the fluorescent dye mepacrine¹⁰¹ or fluorescent platelet monoclonal antibodies¹⁰² directly to whole blood. During experiments, the flow chamber is mounted on an inverted-stage microscope equipped with an epifluorescent illumination attachment and a CCD camera connected to computers for image acquisition and processing. Whole blood is pumped through the chamber, and quantitative values for the number of platelets deposited and the total surface coverage over time are measured to calculate the real-time growth of thrombi.⁶⁸^,⁹⁸ The imaging can be extended to evaluate the surface interactions with larger cells such as leukocytes and transfected mammalian cells. These larger cells are phase bright, and fluorescent illumination is not necessary. Leukocytes and transfected mammalian cells in suspensions can be clearly distinguished by phase-contrast microscopy even if the suspensions are perfused over a cell monolayer immobilized on the surface. The mean velocity of rolling platelets or larger cells may be calculated by overlapping sequential digital images obtained and determining the distance the cells rolled during the period of the image acquisition.¹⁰³

FLOW EFFECTS ON COAGULATION

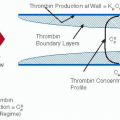
The coagulation cascade is a complex series of linked enzymatic reactions that support the formation of mural thrombi by producing thrombin and fibrin at sites of vascular injury.¹⁰⁴^,¹⁰⁵ The reactions are catalyzed by complexes composed of circulating proteases and surface-associated protein cofactors. The key regulating enzyme complexes and a number of the reaction products form on phospholipid surfaces.¹⁰⁴^,¹⁰⁵^,¹⁰⁶ This surface requirement localizes reactions to certain elements in the subendothelial matrix, as well as membranes of endothelial cells (intact or damaged) and peripheral blood components such as platelets.¹⁰⁶^,¹⁰⁷ The formation of enzyme complexes depends on the delivery of the required circulating protease to the vessel wall where the protein cofactor is immobilized. Under noncomplex flow conditions, the protease may only reach the wall by radial diffusion. Increasing velocity, and therefore increasing shear, enhances the mass transfer of the protease to the surface.⁷⁹^,¹⁰⁶^,¹⁰⁸ Thrombin production measured in a phospholipid/cofactor-coated capillary tube clearly demonstrates the effects of mass transfer on the formation of surface-bound enzyme complexes in the coagulation cascade.¹⁰⁸ The production of thrombin is accelerated by the phospholipid-bound enzyme complex, prothrombinase, formed by circulating factor Xa associating with surface-bound factor Va. In the capillary tube system, the steady-state production level of thrombin can be limited by a low concentration of factor Va bound to the phospholipid surface. When factor Va is limiting, increasing the concentration of circulating factor Xa or increasing the shear does not change the final, steady-state thrombin production values. However, under these conditions, the time to reach the steady-state production values is reduced by increasing the concentration of circulating factor Xa or by increasing the shear rate. These results indicate that shear increases the formation of the prothrombinase complex by increasing the delivery of factor Xa to the surface. When the concentration of the circulating component rather than the surface component is limiting, increasing shear will lead to an increase in steady-state production values. In addition to increasing the supply of circulating components to the vessel surface, increasing shear will increase the removal of species produced at the wall but not bound to the vessel. This may explain the decrease in fibrin deposition on exposed subendothelium observed in response to increasing shear.¹⁰⁹ Alternatively, the decrease in fibrin deposition may be attributed to shear-induced secretion of tissue-type plasminogen activator (tPA) by endothelial cells upstream of the wound.¹¹⁰

Only gold members can continue reading. Log In or Register to continue