To approach answers to these two questions, we must consider quantitative models of the emergence of drug resistance. Drug resistance is a known fact in cancer therapeutics.¹⁶ The first theory concerning the rate of emergence of drug resistance derived from pioneering experiments in bacteriology by Luria and Delbrück in the 1940s. They discovered that different culture dishes of the same bacterial strain developed resistance to bacteriophage infection at different random times before exposure to the viruses.¹⁷ They could measure the percentage of cells that had randomly acquired such resistance by exposing each bacterial culture to the bacteriophage. The percentages varied from culture dish to dish even though all cultures started off with the same number of the same bacteria. They reasoned that cultures that had experienced a mutation earlier in their growth histories had more time to develop a high percentage of resistant bacteria.

The mathematics of this phenomenon can be explained as follows: If a bacterium mutates toward property × with probability x at each mitosis, the probability of the cell not developing property × in one mitosis is P_X(0) = (1 – x). The probability of no mutations toward × occurring in y mitoses is (1 – x)^y. If each mitosis produces two viable cells (i.e., the assumption of no cell loss), it takes (N – 1) mitoses for one cell to grow into N cells. Hence, the probability of not finding any bacteria with the property × in N cells is exp[(N – 1) × ln(1 – x)], which is approximately exp[-x(N – 1)] for small x. Should any cell loss be present, it would take >(N – 1) mitoses to produce N cells, and therefore the probability is <P_X(0) = exp[-x(N – 1)].

Within a decade of Delbrück and Luria’s original observation in bacteria, Law¹⁸ found that this same mathematical pattern applied to the emergence of methotrexate resistance in L1210 cells. Drug (or, at least, antimetabolite) resistance was thus reasoned to be a trait that was acquired spontaneously at random times in the pretreatment growth of this cancer.

Time has not diminished the enthusiasm of scientists for this quantitative concept of acquired hereditable genetic alterations, although the spectrum of possible abnormalities continues to expand. Aneuploidy is an obvious consequence of genomic instability and, like drug resistance, should increase in probability as a function of the number of passages through S phase.^19,20,21 Because the presence of a consequentially large cell-loss fraction should increase the number of passages through S phase in a cell population’s history, the probability of finding significant genetic alterations should increase under those conditions.

In a qualitative sense, the observations and reasoning of Delbrück, Luria, Law, and subsequent scientists had a profound influence on the genesis of the concept of combination chemotherapy²² which is, after all, the central theme of modern medical oncology. When asked to deal with a mature cancer, even at the time of first diagnosis, the therapist could well be faced with a disease heterogeneous in drug sensitivity. The probability of there being resistant clones would be increased by the combination of a high mitotic rate and a high apoptotic rate. In that case, the only hope for tumor eradication would rest with combinations of drugs, each drug hitting a sensitive clone within the tumor mass. This hope is based on the improbability that any one cell could spontaneously become resistant to many different drugs with different biochemical sites of action.²³

The improbability of multiple drug-resistant cells was reexamined quantitatively in 1979 by Goldie and Coldman.^23,24 They first considered simple conditions but later refined their model to include multiple sublines with double or higher orders of drug resistance and the presence of cell loss.²⁵ Their fundamental conclusion can be illustrated by reference to the expression P_X(0) = exp[-x(N – 1)] that we derived earlier: At a tenable mutation rate x = 10^-6, the probability of no mutants in N = 10⁵ cells is approximately 0.9, meaning that most low cell-loss tumor masses of 10⁵ cells are free of drug-resistant cells. However, the probability of finding no drug-resistant mutants in 10⁷ cells is only 4.5 × 10^-5, meaning that it is almost certain that a 10⁷ cell mass harbors at least one drug-resistant mutant. Hence, according to this model, a growth of two logs can transform a tumor from drug curable to drug incurable.

Although created to address the emergence of drug resistance, perhaps a better illustration of the power of this concept concerns a cell’s metastatic ability. Because normal cells cannot survive in an environment other than their natural one, the capability of metastasizing must be an acquired trait and therefore a reflection of genetic lability.²⁶ In primary breast cancer, the most reliable predictor of axillary metastases is tumor size. Only 17% of invasive ductal lesions <1 cm in diameter are metastatic to the axilla, contrasted with 41% of lesions of 2 cm in diameter and 68% of tumors²⁷ of 5 to 10 cm. The presence of axillary metastases, in turn, is the best predictor of eventual metastatic spread. For primary breast cancers that do not involve axillary lymph nodes, the probability of eventual distant metastases is also a function of tumor size. This probability increases sharply when the primary mass in the breast is found to be >1 cm in diameter.²⁸ The volume of 10⁷ cancer cells is approximately 0.01 cc if the whole mass is cancer and approximately 1.0 cc if only 1% is cancer, 99% being benign host tissues such as stromal cells, fibrosis, extracellular secretions, and blood and lymphatic vessels. A 1-cc spherical tumor, the critical size regarding prognosis in node-negative breast cancer, contains a volume of slightly >0.5 cc. This is right in the middle of the range of 0.1 to 1.0 cc described earlier for 10⁷ cells. Hence, clinical observations regarding the probability of metastases fit the Goldie-Coldman model, although other explanations are possible, as described in the penultimate section of this chapter.

As it relates to drug resistance, the Goldie-Coldman model has generated testable predictions. It predicts that a cancerous mass arising from a single drug-sensitive malignant cell has at most a 90% chance of being curable at 10⁵ cells but almost no chance of being curable at 10⁷ cells. Hence, even at the most liberal packing ratios of cancer cells to benign stroma, tumors >1.0 cc should always be incurable with any single agent. The logical development of this idea is that the best strategy is to treat a cancer when it is as small as possible, before its cells can develop resistance. Once treatment is started, as many effective drugs as possible should be applied as soon as possible to prevent cells that are already resistant to one drug from mutating to resistance to others.

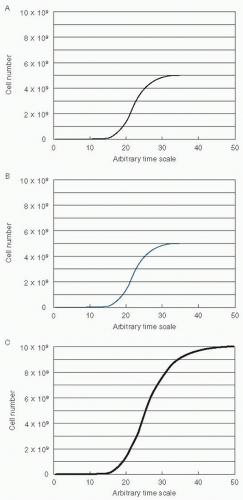
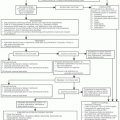
These recommendations are equivalent to the intuitive principles underlying combination chemotherapy, which were originally constructed to deal with drug resistance present at the time of first diagnosis.²⁹ However, Goldie and Coldman went beyond this to suggest a novel treatment plan. They recognized that sometimes many drugs cannot be used simultaneously at good therapeutic levels because of overlapping toxicity or competitive interference. They reasoned that in this case the drugs should be used in a strict alternating sequence. This hypothesis was based on several assumptions in addition to the general assumption that chemotherapeutic failure is because of drug resistance. (The following assumptions are concordant with the general mathematical concept of symmetry.) Imagine that a tumor is comprised of two cell populations, A and B, both of which are growing in a Gompertzian manner (Fig. 2.1). Here, we assume that the A cells (panel A, black line) are sensitive only to therapy A, the B cells (panel B, blue line) are sensitive only to therapy B, and the total tumor growth is a combination of A and B (panel C). The second assumption was that the rate of mutation toward biochemical resistance is constant in both sublines. That is, the A cells mutate toward resistance to A at the same rate as the B cells mutate to acquire resistance to B. The third assumption was that the growth pattern and growth rates of the two sublines were equivalent.³⁰

Let us examine the assumptions, conclusions, and implications of this very important model. Is all chemotherapeutic failure rooted in absolute drug resistance? Much clinical experience challenges this concept. When lymphomas and leukemias recur after chemotherapy-induced remission, they frequently respond to the same chemotherapy again. Patients with Hodgkin disease who experience relapse 18 or more months after they have achieved complete remission from combination chemotherapy have an excellent chance of attaining complete remission again when the same chemotherapy is reapplied.³¹ Similarly, breast adenocarcinomas that relapse from postoperative adjuvant chemotherapy frequently respond to the same chemotherapy. For example, a Cancer and Leukemia Group B (CALGB) protocol treated patients with advanced breast cancer with cyclophosphamide, doxorubicin (Adriamycin), and 5-fluorouracil (CAF) with or without tamoxifen.³² None of these patients had had prior chemotherapy for their advanced disease, but some had had prior adjuvant chemotherapy. Nevertheless, the odds of response, the duration of responses, and the overall probability of survival were unaffected by a patient’s past history of adjuvant chemotherapy. A similar series of observations resulted from clinical trials at the National Cancer Institute in Milan. Patients in whom stage IV breast cancer developed after adjuvant cyclophosphamide, methotrexate, and 5-fluorouracil (CMF) responded as well to CMF for advanced disease as those who had been previously randomized to be treated with radical mastectomy alone.³³ These findings mean that breast cancers that regrow after exposure to adjuvant CMF are not universally resistant to CMF.³⁴ Hence, not all chemotherapeutic failures can be because of permanent drug resistance. In addition, some patients respond to standard doses of chemotherapeutic regimens following relapse after higher doses of chemotherapy used in an autologous bone marrow
transplant setting. Although it is possible that some cancers escape cure because of a temporary absolute drug resistance that reverses over time, it is more likely that sensitive cells are somehow not completely eradicated by drugs to which they are still sensitive.

Before we consider the implications of this latter possibility, let us return to the specific conclusions of the Goldie-Coldman model. Are tumors >1.0 cc always incurable with single drugs? The answer is no. Two rapidly growing cancers, gestational choriocarcinoma and Burkitt lymphoma, have been cured with single drugs, even when therapy is initiated at tumor sizes³⁵ much >1.0 cc. Other counterexamples to the incurability of large cancers are childhood acute lymphoblastic leukemia, most pediatric cancers, adult lymphomas, and germ cell tumors, which are frequently cured with couplets and triplets of drugs. Hence, the presence of 10⁷ cells does not always signify incurability.

With respect to the previous discussion regarding metastatic potential, neither does the presence of 10⁷ cells always signify that the tumor must have acquired the ability to thrive in distant sites. In fact, the whole notion that cancers develop deleterious mutations rapidly as they grow is challenged by observations of the probability of metastatic disease. For example, standard practice until the late 19th century was not to operate on primary breast cancer but to allow it to grow unperturbed.³⁶ Under such conditions, the cancers would almost always become metastatic. In the 20th century, radical mastectomy was invented, later to be replaced by simple mastectomy with axillary dissection and now lumpectomy with regional radiotherapy. Long-term follow-up of patients being treated by radical mastectomy in the middle of the century indicated that the natural history of untreated breast cancer could be altered by surgical removal. Even without adjuvant systemic treatment of any sort, at 30 years of follow-up >30% of patients are found to be alive and free from disease.^37,38 The mortality, initially approximately 10% per year, drops gradually to approximately 2% per year by the 25th year³⁹ and after 30 years is indistinguishable from that of the general population.^40,41 The fact that the development of systemic disease is so common means that most breast cancers have already developed metastases by the time of initial presentation. Yet the fact that not all cancers develop this ability means that the previous calculations for P_X(0) for 10⁷ cells cannot be realistic.

Let us look at this issue another way. If local control is poor and the cancer cells in the breast are not completely removed or destroyed so that they eventually regrow to a clinically appreciable mass, will they always mutate rapidly to produce metastatic clones? This question was asked by a protocol of the National Surgical Adjuvant Breast and Bowel Project (NSABP), in which some patients with primary disease were treated by lumpectomy without radiotherapy.⁴² The local relapse rate was significant, but survival was close to that of patients treated adequately de novo by lumpectomy and immediate radiotherapy. Some metastases from residual cancer should be expected, even if the residual cells did not progress in their ability to release metastatic clones; therefore, longer follow-up might eventually reveal a higher rate of distant metastases. However, the lack of a blatant difference so far indicates that tumor can remain in a breast, grow in the breast, and yet not develop metastatic cells at a very high rate, as would be predicted by the Goldie-Coldman model. In addition, a recent meta-analysis of 25 randomized trials of postmastectomy radiotherapy versus no radiotherapy demonstrated a small but significant improvement in overall survival with radiation for patients with node-positive disease.⁴³ The important observation is that the benefits, although real, are small. This means that tumor
can metastasize from the chest to other sites, but this does not occur at a very high rate.

Returning to the issue of drug sensitivity, what is the evidence that chemotherapy must be started as soon as possible after diagnosis to be effective? An early trial in the treatment for acute leukemia found that the response to an antimetabolite was the same if that drug was used first or sequentially after the use of a different antimetabolite.²² Hence, delay was not harmful, which contradicts the prediction of the Goldie-Coldman model. A randomized trial by the International (Ludwig) Breast Cancer Study Group found a similar result. Patients with node-positive breast cancer were given either 7 months of chemotherapy starting within 36 hours of surgery or 6 months of chemotherapy beginning approximately 4 weeks after surgery.⁴⁴ Because the results were the same, the delay was not harmful here either.

Similarly, patients with metastatic breast cancer whose disease responded completely to standard-dose chemotherapy were randomized to immediate high-dose chemotherapy and hematopoietic stem cell reinfusion (i.e., autotransplantation) versus observation.⁴⁵ On relapse, most of the patients who were originally randomized to standard-dose chemotherapy were subsequently treated with the same high-dose chemotherapy. Final results demonstrate a greater event-free survival for those in the immediate transplantation arm versus the delayed transplantation arm but no significant difference in overall survival. Patients with stage II nonseminomatous testicular cancer were randomized after retroperitoneal lymph node dissection to either two cycles of cisplatin combination chemotherapy or to untreated observation.⁴⁶ At a median follow-up of 4 years, 49% of patients who were randomized to observation relapsed, in contrast to only 6% of patients randomized to adjuvant chemotherapy. Yet the response of relapsing cases to subsequent chemotherapy was so excellent that no significant survival differences were found in the cure rate between the two approaches. Hence, most testicular carcinomas retained their chemosensitivity in spite of the delay in the initiation of treatment. In all of these examples, cells that are residual after surgery grow unimpeded without rapidly developing drug-resistant mutants.

Let us look at another conclusion of the model. Must all drugs in an adjuvant regimen be introduced early to have a biologic impact? A trial by the CALGB has concluded that this is not the case.^47,48 Patients with primary breast cancer and positive axillary lymph nodes were treated with 8 months of adjuvant CMF plus vincristine and prednisone (CMFVP) followed by either more CMFVP or 6 months of the combination of vinblastine, doxorubicin, thiotepa, and the androgen fluoxymesterone (Halotestin; VATH). Patients who received the crossover therapy, especially those with four or more involved axillary nodes, experienced a significantly improved disease-free survival. Clearly, overwhelming cellular resistance to the agents in VATH did not develop rapidly in the cells that were not eradicated by the CMFVP. Seeming to contradict these results, a trial in Milan found no advantage to a sequence of doses of doxorubicin after CMF for patients with one- to threeinvolved nodes.⁴⁹ Moreover, the collection of patients with better prognoses may not be the ideal population for testing such hypotheses. Chemotherapy works by reducing the annual odds of recurrence and death.¹³ If the crossover works for all patients by reducing the rate of relapse by a certain percentage of that rate, those with lower rates of relapse without the crossover would experience a lower absolute benefit from the crossover than those at higher risk for relapse. Hence, the effect would exist in good-prognosis patients but be more apparent in those with poorer prognoses. One could also postulate from the Goldie-Coldman hypothesis that administration of chemotherapy preoperatively may be more beneficial. Indeed, their model was one of the prime reasons why preoperative chemotherapy was considered as a potentially useful approach. However, several trials have found no significant improvement in clinical outcome with the administration of preoperative chemotherapy for early stage operable breast cancer.^50,51,52

The unique assertion of the Goldie-Coldman model, the hypothesis most commonly linked to this theory, concerns the potential superiority of alternating chemotherapy sequences. In the clinic, however, this strategy has not been demonstrated to be superior. Little benefit has been found in numerous attempts to use alternating chemotherapy sequences in the treatment for small-cell lung cancer.⁵³ In the treatment for diffuse, aggressive non-Hodgkin lymphoma, a National Cancer Institute trial found no advantage to a prednisone, methotrexate, doxorubicin, cyclophosphamide, etoposide (ProMACE)-mechlorethamine, vincristine, procarbazine, prednisone (MOPP) hybrid, which delivered eight drugs during each monthly cycle over a full course of ProMACE followed by MOPP.⁵⁴ In the treatment for advanced Hodgkin disease, MOPP has been compared with MOPP alternating with doxorubicin, bleomycin, vinblastine, and decarbazine (ABVD), an effective first-line therapy and salvage regimen for patients whose disease is refractory to MOPP.^55,56 MOPP-ABVD was found to be superior to MOPP in producing complete remission in chemotherapy-naive patients and in freedom from progression and survival.^57,58 An ABVD control arm was not studied. It is interesting, therefore, that the CALGB found that the complete remission rate and failure-free survival from MOPP-ABVD was better than that from MOPP alone but equivalent to ABVD alone.⁵⁹

Considering these results, the superiority of MOPP-ABVD and of ABVD over MOPP alone may have been because of differences in dose received. No advantage was found to the alternating scheme MOPP-ABVD over ABVD alone. A similar result was found by the National Cancer Institute in its study of MOPP alternating with lomustine, doxorubicin, bleomycin, and streptozocin, which was equivalent to the use of MOPP alone.⁶⁰ An intergroup trial found that a hybrid of MOPP-ABVD was superior in complete remission rate, failure-free survival, and overall survival to MOPP followed by ABVD.⁶¹ The doses of MOPP were similar in both arms, although the doses of doxorubicin were somewhat lower in the sequential arm.

As with the lymphomas, alternating strategies have not proved superior in the treatment for breast cancer. The VATH regimen is active against tumors that relapse from, or fail to respond to, CMF and thereby meets the criterion of noncross resistance. Yet in patients with advanced disease, the CALGB
found no advantage to CMFVP alternating with VATH over CAF or VATH alone.⁶²

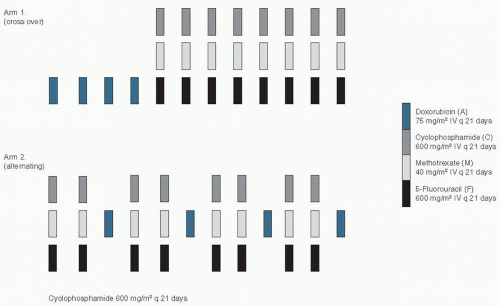
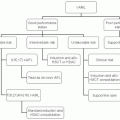
An interesting variant on the alternating chemotherapy idea concerns the use of drugs in sequenced courses. In the adjuvant setting, a direct comparison of alternating and sequential chemotherapy was conducted in Milan. The sequential approach was described earlier by reference to the use of VATH after CMFVP by the CALGB, also in the adjuvant setting.⁴⁷ The National Cancer Institute in Milan had had a previous positive experience with sequential chemotherapy,⁶³ but this was not a randomized trial and therefore did not test the concept.⁶⁴ To test the concept, Bonadonna and his colleagues⁶⁵ randomized women with early breast cancer that involved four or more axillary lymph nodes to one of two treatment arms. Arm I prescribed four 3-week cycles of doxorubicin (A) followed by eight 3-week cycles of intravenous (IV) CMF, whereas arm II patients received two cycles of intravenous IV CMF alternating with one course of doxorubicin (Fig. 2.2). The total amounts of doxorubicin and CMF in both arms were equal, as were the durations of therapy and the spacing of cycles. Remarkably, the patients who received arm I had a higher disease-free survival and a higher overall survival than those on arm II. At equivalent received doses, alternating courses of chemotherapy were found to be inferior to a crossover therapy plan.⁶⁶ To illustrate this further, in Figure 2.3 we see two growth curves of blue and black cells, which make up a tumor mass. The “blue” cells are sensitive to the therapy symbolized by the blue arrows (e.g., doxorubicin) but are resistant to the therapy symbolized by the black arrows (e.g., CMF). Similarly, the “black” cells are sensitive to the therapy symbolized by the black arrows (CMF), but are resistant to the therapy symbolized by the blue arrows (doxorubicin). In panel A, the treatment is administered sequentially, as per arm I (crossover) in the trial described above. In panel B, the alternating treatment approach is used as per arm II in the study above. It is clear that the log-kill from the sequential approach (panel A) is greater in the “blue” cancer cells and not inferior in the “black” cells. Hence, the overall cytoreduction is greater with the sequential approach, as illustrated by the time for the blue curve to reach 10¹⁰ cells (dashed line).This model illustrates how sequential therapy can result in better outcomes for patients and explain the result in the clinical trial described earlier.

The sequential chemotherapy strategy is also useful in the treatment for leukemia. In adult acute myelogenous leukemia, complete remission is obtained commonly with cytarabine plus anthracyclines. However, the median remission duration tends to be short. Given at low doses, postremission maintenance therapy is relatively ineffective, and this is not improved by a longer duration of treatment (32 months vs. 8 months of the same therapy).^67,68 A more recent trial questioned the effectiveness of intensive rather than conventionally
dosed postremission chemotherapy, basing its rationale on the steep dose-response curve for cytarabine.⁶⁹ The trial studied 596 of 1,088 patients who had achieved complete remission from standard induction chemotherapy and found that the highest-dose regimen was the most effective of three different dose schedules of cytarabine. In fact, the best results were comparable to those reported in patients with similar disease who were treated by allogeneic bone marrow transplantation during first remission.⁷⁰ In support of this result, the Children’s Cancer Study Group found that intensive induction followed sequentially by intensive consolidation and later intensification was superior to other strategies in the treatment for childhood acute lymphoblastic leukemia.⁷¹