Modeling of Diabetes Progression

(1)

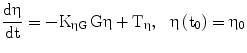
$\frac{{{\rm{d}}\upeta }}{{{\rm{dt}}}} = - {\rm{K}}_{{{\rm{\upeta G}}}} \,{\rm{G \upeta }} + {\rm{T}}_{{\rm{\upeta }}},\,\,\,\,{\rm{\upeta }}\left( {{\rm{t}}_{0} } \right) = {\rm{\upeta }}_{0}$

(2)

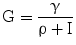
${\rm{G}} = \frac{{\rm{\upgamma }}}{{{\rm{\uprho }} + {\rm{I}}}}$

(3)

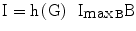
${\rm{I}} = {\rm{h}}\left( {\rm{G}} \right)\,\,\,{\rm{I}}_{{\hbox{max} \,{\rm{B}}}} {\rm{B}}$

(4)

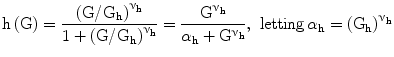
${\rm h\left( G \right)} = \frac{\rm{\left( {{G \mathord{\left/ {\vphantom {G {G_{h} }}}\right. \kern-0pt} {G_{h} }}} \right)^{{\upnu_{h} }} }}{\rm{1 + \left({{G \mathord{\left/ {\vphantom {G {G_{h} }}} \right. \kern-0pt} {G_{h} }}}\right)^{{\upnu_{h} }} }} = \frac{\rm {G^{{\upnu_{h} }} }}{\rm{\alpha_{h} + G^{{\upnu_{h} }} }},\,\,{\rm letting}\,{\rm \alpha_{h} = \left( {G_{h} } \right)^{{\upnu_{h} }}}$

(5)

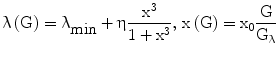
$\uplambda \left({\rm G} \right) = \uplambda_{\hbox{min} } + \upeta \frac{{\rm x^{3} }}{{\rm 1 + x^{3} }},\,{\rm x}\left( {\rm G} \right) = {\rm x_{0}} \frac{\rm G}{{\rm G_{\uplambda } }}$

(6)

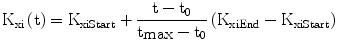
${\rm K_{xi}} \left( {\rm t} \right) = {\rm K_{xiStart}} + \frac{\rm {t - t_{0} }}{{{\rm t}_{\hbox{max} } - {\rm t_{0}} }}\left( {\rm {K_{xiEnd} - K_{xiStart} }} \right)$

(7)

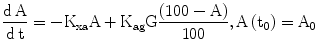
$\frac{\rm {d\,A}}{\rm{d\,t}} = - {\rm K_{xa} A + K_{ag}} {\rm G}\frac{{(100 - {\rm A})}}{100},{\rm A\left( {t_{0} } \right) = A_{0}}$

(8)

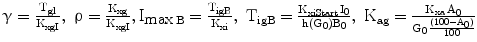with $\upgamma = \frac{\rm {T_{gl} }}{\rm{K_{xgI} }},\,\,\uprho = \frac{\rm{K_{xg} }}{\rm{K_{xgI} }},{\rm I}_{{\hbox{max} \,{\rm B}}} = \frac{\rm{T_{igB} }}{\rm{K_{xi} }},\,\,{\rm T_{igB}} = \frac{\rm{K_{xiStart} \,I_{0} }}{\rm{h\left({G_{0}} \right)B_{0}}},\,\,{\rm K_{ag}} = \frac{\rm{K_{xa} \,A_{0}}}{\rm{G_{0} \,\frac{\rm{(100 - A_{0})}}{100}}}$ , and λ_max = λ_min + η.

The definitions and units of all state variables and parameters are reported respectively in Tables 1 and 2.

Table 1

Definition of state variables

State variables: symbol and meaning	Units
t, time	[mo]
Β, β-cell mass as Millions of active β-cells	[Mc]
I, fasting serum insulin concentration (monthly average)	[pM]
G, fasting plasma glucose concentration (monthly average)	[mM]
h, glucose effect on pancreas	[#]
x, replaces Glucose variations with variations of a scale-free pure number	[#]
λ, net rate constant for β-cell growth (or decay), resulting from the difference between production (replication) rate and mortality (apoptosis) rate	[mo⁻¹]
η, possible lambda excursion, represents pancreatic replication ‘reserve’	[mo⁻¹]
K_xgI, second-order insulin-dependent glucose tissue uptake rate per pM insulin, represents insulin sensitivity	[min⁻¹/pM]
γ, resistance to insulin as the number of mM of glucose at which glycemia stabilizes for a single pM of insulinemia	[mM * pM]
λ_max, maximum (positive) value of λ, i.e. the maximum possible difference between replication rate and apoptosis rate	[mo⁻¹]
I_maxB, insulin attainable levels, expressed as the maximal contribution of a million β-cells to fasting insulin plasma concentration	[pM/Mc]
A, glycosylated Haemoglobin, HbA1c (monthly average)	[%]

Table 2

Definition of model parameters

Model parameters: symbol and meaning	Units
B₀ = B(t₀): initial condition on β-cell mass	[Mc]
B_max: maximal size of β-cell mass	[Mc]
I₀: insulinema at age t₀	[pM]
G₀: glycemia at age t₀	[mM]
G_λ: the glycemia of maximal sensitivity of the regulation of β-cell population dynamics	[mM]
T_gl: liver glucose output. This parameter can be considered as a constant basal, insulin-independent glucose output, while insulin-dependent glucose output (decreasing with increasing levels of insulin) is taken into account through the action of KxgI	[mM/min]
K_xg (FAST): first-order insulin-independent glucose tissue uptake rate	[min⁻¹]
T_igB (FAST): maximal pancreatic insulin secretion per million β-cells	[pM/min/Mc]
K_xi (FAST): apparent first-order elimination rate constant for insulin	[min⁻¹]
K_xiStart: apparent first-order elimination rate constant for insulin at baseline (e.g. at age 18 years)	[min⁻¹]
K_xiEnd: Apparent first-order elimination rate constant for insulin at the end of a normal life (e.g. at age 90 years)	[min⁻¹]
K_xgI0: value of K_xgI at t₀	[min⁻¹/pM]
t_I: time of midpoint Κ_xgI decrease (time at 0.5 * K_xgI0)	[mo]
ν_I : exponent for the decrease in K_xgI	[#]
ρ: ratio of 1st order to 2nd order (Insulin Dependent) rate constants for tissue glucose uptake from plasma	[min⁻¹/(min⁻¹ /pM)] = pM
I_maxB0: value of I_maxB at t₀	[pM/Mc]
λ_min: the minimum (negative) value of λ, i.e. the maximum net apoptosis rate	[mo⁻¹]
η₀: value of η at t₀ (determined)	[mo⁻¹]
T_η: the spontaneous recovery rate of the pancreas	[mo⁻²]
K_ηG: Rate constant expressing pancreatic glucose toxicity	[mo⁻¹mM⁻¹]
G_h: centering glucose concentration for Hill-shaped glycemia effect on pancreatic insulin release, set to 9 mM	[mM]
ν_h: power coefficient for Hill-shaped glycemia effect on pancreatic insulin release, set to 4 in order to achieve linearity between 5 and 10 mM, essentially zero before 3.5 mM, essentially saturated above 25 mM	[#]
h₀: The value of the h(G) function at t₀ (determined)	[#]
ξ: the scaling factor for the X support variable, computed so as to center the X sigmoid curve on the value λ = 0	[#]
A₀ = A(t₀): initial condition on glycosylated Haemoglobin (HbA1c).	[%]
K_ag : the rate constant of production of glycosylated haemoglobin from circulating glucose	[%/mo/mM]
K_xa: the spontaneous elimination rate constant of (glycosylated) Haemoglobin	[mo⁻¹]
t₀: starting age, with system at equilibrium, in months	[mo]
t_η10, Half-life of Pancreatic reserve at 10 mM Glucose	[mo]

Equations 3 and 4 simply state that prevailing glycemias at any historical moment are inversely related to the prevailing insulinemias, while prevailing insulinemias are directly related to (an increasing function of) prevailing glycemias as well as being directly related to available β-cell mass and secretory capacity. The “prevailing” glycemia and insulinemia levels described in the model do not strictly refer to either fasting or post-prandial values, but are in fact representative of daily steady-state blood concentrations, hourly oscillations being averaged out when considering the evolution of the system over a time span of months or years. Prevailing glycemia and insulinemia are derived as equilibrium values, given the existing level of insulin sensitivity and the current functional β-cell mass available for insulin secretion: they substantially reflect real-life post-absorptive values.

The model hypothesizes, in a straightforward population dynamics fashion, that the variation in β-cell mass B (Eq. 1) is proportional to current mass in logistic growth fashion, with carrying capacity B_max, multiplied by a net-growth rate λ.

In turn, λ depends (Eq. 6) on prevailing glucose concentrations, in the sense that it varies from a minimum negative value (λ_min) to a maximum value that is dependent both on the prevailing pancreatic reserve described below (i.e. λ_max = λ_min + η) and on glucose level according to a sigmoidal 3rd-degree Hill function, with λ = λ_min when G = 0, and λ tending to λ_max as G tends to infinity.

The Hill function is normalized (it is a function of x rather than G) so as to have maximum slope at the glycemia value G_λ. If G_λ is approximately equal to normal fasting glycemia (e.g. around 5 mM), this is the same as assuming that the regulation mechanisms of the pancreas work optimally in a neighborhood of the target fasting glycemia.

The term η represents the ‘pancreatic reserve’, i.e. the current ability of the pancreas to increase its β-cell proliferation rate if sufficiently stimulated by the ambient glucose concentration. Pancreatic reserve, however, is not a fixed quantity: it varies with time (Eq. 2), in such a way that it always tends to an equilibrium level. This equilibrium is the result of two competing forces: glucose-toxicity-induced shrinkage of pancreatic reserve and spontaneous recovery of the pancreas. Pancreatic reserve (at equilibrium) is thus inversely proportional to prevailing glycemias. In other words, Eq. 6 prescribes that hyperglycemia will always acutely stimulate pancreatic β-cell replication (to the extent that this is allowed by the current pancreatic reserve level), while Eq. 2 prescribes that, chronically, sustained hyperglycemia will make pancreatic reserve decrease. Notice that, if pancreatic reserve is sufficiently damaged, i.e. if η < −λ_min, then λ_min + η < 0 and β-cell population would decline, in the absence of therapy, no matter what the prevailing glucose concentration. It should be kept in mind that this effect could well stem both from an anti-proliferative and from a pro-apoptotic original lesion.

Equations 3 and 4 derive, as hinted to above, from the equilibrium condition for glycemia and insulinemia respectively, given that the model focuses on changes over months or years. At each point in slow time, therefore, the fast dynamics of glucose and insulin are assumed to be at equilibrium. This equilibrium may be conceived as being the average glycemia produced by the average insulinemias and by the current levels of insulin sensitivity. Conversely, average insulinemia is determined by the prevailing glycemias, by the β-cell mass available at the time, and by a coefficient of insulin production at maximal stimulation per β-cell mass unit. It should be pointed out that using fasting or average glucose and insulin concentrations amounts conceptually to the same thing, as we only need indicator quantities for the prevailing state of the system over a period of a day or a week.

The function h (Eq. 5) captures the hypothesis that glycemia stimulates insulin production by the pancreas in a sigmoidal fashion, starting at zero, sloping up approximately linearly between 5 and 10 mM glycemia, and approaching asymptotically a maximum as glycemia increases.

We found it necessary to stipulate that, as observed in the literature [30], the apparent first order rate constant of elimination of insulin from plasma decreases with age (Eq. 7): this allows the model to replicate the observed decline of insulin secretory function, associated with preserved or even increased levels of serum insulin, with advancing age [31].

The variable γ (inversely related to the index of insulin sensitivity K_xgI) expresses resistance to insulin, as the concentration at which glucose stabilizes for each pM of insulin concentration.

For the purposes of the present simulations, it has been assumed that the insulin-independent glucose tissue uptake rate constant K_xg is small (within the range of considered glycemias) compared to insulin-dependent glucose uptake [19], and that consequently the ratio ρ is also approximately zero.

The variable I_maxB is the maximal contribution of a million β-cells to fasting plasma insulin concentration. Its value is determined by the maximal insulin secretion rate per million β-cells T_igB (determined by equilibrium conditions at t₀), and by the actual first-order apparent rate of elimination of insulin from plasma, K_xi, which is considered here to decrease with age (linearly, in first approximation), as mentioned above. It should be kept in mind that T_igB in our simulations is made to decrease when supposing primary defects of insulin secretory function with advancing age, and conversely it is made to increase in response to secretagogues.

In order to link observable glycated hemoglobin with the glucose dynamics, a simple linear model of the kinetics of HbA1c (indicated as A in Eq. 8) is part of DPM, with increase determined by prevailing glycemias and by the concentration of native HbA0, and decrease linearly determined by the continuous destruction of red blood cells.

2.1 Parameter Assessment

Parameters for the model have been carefully assessed from literature data and from the results of directed experiments, with the goal of maintaining consistency among the several sources. Only human data have been used. Although limited information was available for some parameters, most were based on empirical observations derived using well-established methodologies. The majority of parameters were obtained from in vivo studies but in a few cases only in vitro or post-mortem data were available. Preference was generally given to studies with larger numbers of subjects, but study quality and design were also considered (e.g. age range of study population, level of validation of key measurements). For each parameter, we sought to identify a typical value, reflecting a non-diseased population, keeping in mind that the range of reasonable values for each parameter would include those seen in diabetic individuals. Typical values and ranges at time = t₀ were generally taken from data obtained in young, healthy adults (age 18–30).

Parameter values used in this simulation were as reported in [29], with the following specifications. Moderate secretion and sensitivity defects were assumed to have a minimum reachable value of the corresponding coefficients at 15 % normal, whereas severe defects were supposed to cause a decrease of the coefficient down to 2.5 % normal. In both cases the age at 50 % defect was assumed to be 25 years. The threshold of glycemia for the diagnosis of diabetes was 7 mM. Proportional improvement by classical sensitizers or secretagogues was assumed to be 50 % with respect to the current “natural” value as determined by the progression of disease. Definitive improvement of insulin sensitivity produced by bariatric surgery was assumed to 7.5 % of normal (i.e. a small fraction of supposedly perfect insulin sensitivity as seen in young age) above the current “natural” value due to age and disease. Definitive decrease of glucose toxicity produced by β-cell protectors was assumed to be 20 % of normal.

The model’s numerical integration, starting with given parameter values, has been implemented in a mixed Matlab (© 1994–2007 The MathWorks, Inc.) and C/C++ (GCC, © Free Software Foundation, Inc.) environment, and is freely available as a service to academic users through the CNR IASI BioMatLab website [32].

3 Results

3.1 Qualitative Analysis of the Behavior of Solutions

The original published model [24] was proven to admit three equilibrium points: a physiological steady-state, which is locally asymptotically stable, consisting of the (normal) basal (i.e. ‘early-life’) values of glycemia and insulinemia G_b and I_b; a pathological ‘severe diabetes’ steady-state, which is also locally asymptotically stable, consisting of zero levels of β-cell mass and insulinemia, to which there corresponds a hyperglycemic state (G_h > G_b); and an unstable saddle point, with intermediate glycemia (G_b < G_s < G_h).

Only gold members can continue reading. Log In or Register to continue