(1)
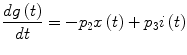
(2)
The physiological interpretation of the MM parameters can be made in terms of insulin-dependent and insulin-independent processes that enhance glucose uptake and suppress net glucose output. The parameter p 1, termed “glucose effectiveness” SG, represents the insulin-independent effect, while the insulin-dependent effect is represented by the ratio p 3/p 2 (in min−1/μUml−1) and is termed “insulin sensitivity” SI. The values of SG and SI are typically estimated from IVGTT data and the MM has proven to be successful in a clinical context, requiring a relatively simple test procedure [5]. Nonetheless, the accuracy and physiological interpretation of the MM parameter estimates has been questioned because of the use of a single compartment for glucose kinetics [10, 11].
The MM, as formulated in Eqs. (1) and (2), does not include an equation describing the secretion of insulin from pancreatic beta cells in response to an elevation in blood glucose concentration, i.e., it is an open-loop model, which may be used along with properly designed experimental protocols (IVGTT) for parameter estimation. However, the actual glucose metabolism process is a closed-loop system, except in conditions of severe Type I diabetes where the pancreatic beta cells are considered totally inactive. In order to account for this, an insulin secretion equation may be included, as described below (closed loop MM or AMM). Limitations of the MM (and the AMM) include the absence of an explicit glucogenic component reflecting production of new glucose by the liver in response to elevated plasma insulin and/or glucose (such as the model presented in [26]) and the associated glucagon secretion process (from the alpha cells of the pancreas) among others. The aggregate effect of these processes, as well as the effect of other factors (free fatty acids, epinephrine etc.), can be incorporated by “disturbance” terms that are added to the glucose rate and insulin action equations.
2.2 Closed-Loop Compartmental Model: The Augmented Minimal Model
The closed-loop nature of insulin-glucose interactions requires the incorporation of an additional equation describing the insulin secretion dynamics by the pancreatic beta cells. Of several equations that have been proposed [4, 39, 41, 42, 45], we select one that utilizes a threshold function, similar to the one reported in [42]. The resulting closed-loop model becomes:
![$$\frac{dg\left( t \right)}{dt} = - p_{1} g\left( t \right) - x\left( t \right)\left[ {g\left( t \right) + g_{b} } \right]$$](/wp-content/uploads/2017/04/A310669_1_En_1_Chapter_Equ3.gif)
![$$\frac{dx\left( t \right)}{dt} = - p_{2} x\left( t \right) + p_{3} \left[ {i\left( t \right) + r\left( t \right) } \right]$$](/wp-content/uploads/2017/04/A310669_1_En_1_Chapter_Equ4.gif)
![$$\frac{dr\left( t \right)}{dt} = - ar\left( t \right) + \beta T_{h} \left[ {g\left( t \right)} \right]$$](/wp-content/uploads/2017/04/A310669_1_En_1_Chapter_Equ5.gif)
where r(t) is the secreted insulin by the pancreatic beta cells in response to an elevation in plasma glucose concentration and i(t) correspond to insulin concentration changes due to externally administered insulin. The secretion is triggered by elevated plasma glucose concentrations according to the threshold function T h [g(t)] defined as:
![$$T_{h} \left[ {g\left( t \right)} \right] = \left\{ {\begin{array}{*{20}l} {g\left( t \right) - \theta } \hfill & {g\left( t \right) \ge \theta } \hfill \\ 0 \hfill & {otherwise} \hfill \\ \end{array} } \right.$$](/wp-content/uploads/2017/04/A310669_1_En_1_Chapter_Equ6.gif)
where θ corresponds to the glucose concentration value above which insulin is secreted. The dynamics of this triggered secretion process and the kinetics of the secreted insulin are described (in first approximation) by the kinetic constant a (in min−1) in Eq. (5). The parameter β (in μU min−1/ml per mg/dl) determines the rate of insulin secretion (i.e. the strength of the feedback pathway). Note that some alternative similar models [4, 41] of insulin secretion include a time-varying term that multiples the last term of Eq. (5) with t. This is based on the hypothesis that the rate of insulin secretion in response to hyperglycemia increases linearly with time. However, this term may not admit a steady-state solution but instead result in unbounded state variable values for physiologically reasonable values of the model parameters. This is not plausible; therefore, it should be taken into account when constructing models that are intended to be physiologically realistic, as discussed in more detail in the chapter by Panunzi and de Gaetano in the present volume.
![$$\frac{dg\left( t \right)}{dt} = - p_{1} g\left( t \right) - x\left( t \right)\left[ {g\left( t \right) + g_{b} } \right]$$](/wp-content/uploads/2017/04/A310669_1_En_1_Chapter_Equ3.gif)
(3)
![$$\frac{dx\left( t \right)}{dt} = - p_{2} x\left( t \right) + p_{3} \left[ {i\left( t \right) + r\left( t \right) } \right]$$](/wp-content/uploads/2017/04/A310669_1_En_1_Chapter_Equ4.gif)
(4)
![$$\frac{dr\left( t \right)}{dt} = - ar\left( t \right) + \beta T_{h} \left[ {g\left( t \right)} \right]$$](/wp-content/uploads/2017/04/A310669_1_En_1_Chapter_Equ5.gif)
(5)
![$$T_{h} \left[ {g\left( t \right)} \right] = \left\{ {\begin{array}{*{20}l} {g\left( t \right) - \theta } \hfill & {g\left( t \right) \ge \theta } \hfill \\ 0 \hfill & {otherwise} \hfill \\ \end{array} } \right.$$](/wp-content/uploads/2017/04/A310669_1_En_1_Chapter_Equ6.gif)
(6)
2.3 Volterra-Type Models
The Volterra-Wiener framework has been employed extensively for modeling nonlinear physiological systems [30]. In this context, the input-output dynamic relationship of a causal, nonlinear system of order Q and memory M is described by the Volterra functional expansion:
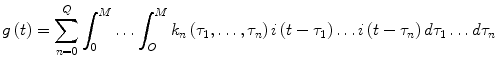
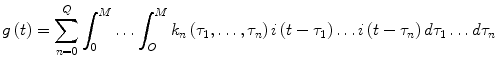
(7)
The Volterra model can be formulated in discrete-time as follows:
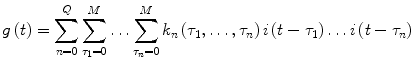
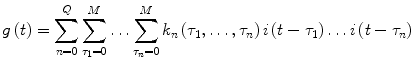
(8)
In both the above models (Eqs. 7 and 8), i(t) and g(t) are the input and output of the system at time t (deviations of plasma insulin and glucose concentrations from their basal values, respectively). The unknown quantities of the Volterra model that are estimated from the input-output data are the Volterra kernels k n (τ1,…, τ n ). The first-order kernel (n = 1) is the linear component of the system dynamics, while the higher order kernels (n > 1) form a hierarchy of the nonlinear dynamics of the system. The highest order Q defines the nonlinear order of the system. Many physiological systems can be described adequately by Volterra models of relatively low order (second or third) [30]. The Volterra-Wiener approach is well-suited to the complexity of physiological systems since it yields data-true models, without requiring a priori assumptions about system structure.
Among various methods that have been developed for the estimation of the discrete-time Volterra kernels (Eq. 8), a Volterra-equivalent network in the form of the Laguerre-Volterra Network (LVN) is selected because it has been proven to be an efficient approach that yields accurate representations of high-order systems in the presence of noise using short input-output records [31]. The LVN model consists of an input layer of a Laguerre filter-bank and of a hidden layer with K hidden units with polynomial activation functions (Fig. 1) [31]. At each discrete time t, the input signal i(t) (insulin) is convolved with the Laguerre filter-bank and weighted sums of the filter-bank outputs V j (where v j = i * b j , * denotes convolution and b j is the j-th order discrete-time Laguerre function) are transformed by the hidden units through polynomial transformations.
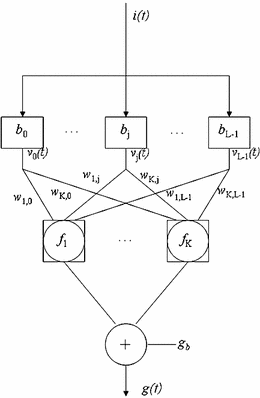

Fig. 1
The Laguerre-Volterra network. The system input i(t) is convolved with a Laguerre filter bank with impulse responses b j , the outputs of which (v j (n)) are fed into a layer of K hidden units with polynomial activation functions f K that produce the system output g(t)
The model output g(t) (glucose) is formed as the summation of the hidden unit outputs z k and a constant corresponding to the glucose basal value g b :
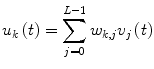
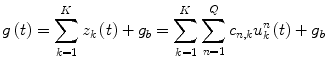
where L is the number of functions in the filter bank and w k,j and c n,k are the weighting and polynomial coefficients respectively. The insulin and glucose time- series are used to train the LVN model parameters (w k,j , c n,k and the Laguerre parameter which determines the Laguerre functions dynamic properties) with a gradient-descent algorithm, as described in [31].
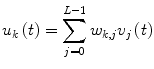
(9)
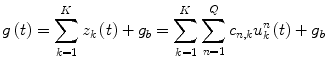
(10)
The equivalent Volterra kernels are then obtained in terms of the LVN parameters as:
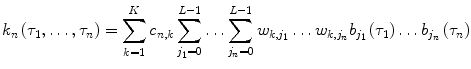
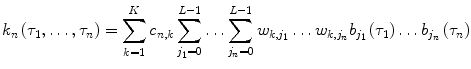
(11)
The structural parameters of the LVN model (L, K, Q) are selected on the basis of the normalized mean-square error (NMSE) of the output prediction achieved by the model, defined as the sum of squares of the model residuals divided by the sum of squares of the demeaned true output. The statistical significance of the NMSE reduction achieved for model structures of increased order/complexity is assessed by comparing the percentage NMSE reduction with the alpha-percentile value of a chi-square distribution with p degrees of freedom (p is the increase of the number of free parameters in the more complex model) at a significance level alpha, typically set at 0.05.
The LVN representation is equivalent to a variant of the general Wiener-Bose model termed the Principal Dynamic Mode (PDM) model. The PDM model consists of a set of parallel branches, each one of which is the cascade of a linear dynamic filter (PDM) followed by a static nonlinearity [29, 30]. Each of the K hidden units of the LVN corresponds to a separate branch and defines the respective PDM p k (t) and polynomial nonlinearity f k(.). This leads to model representations that allow physiological interpretation, since the resulting number of branches is typically low in practice. According to the PDM model form, the insulin input signal is convolved with each of the PDMs p k (t), where k = 1, …, K and 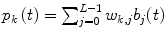 , and the PDM outputs u k are subsequently transformed by the respective polynomial nonlinearities f k (.) to produce the model-predicted blood glucose output (the asterisk denotes convolution) [30]:
, and the PDM outputs u k are subsequently transformed by the respective polynomial nonlinearities f k (.) to produce the model-predicted blood glucose output (the asterisk denotes convolution) [30]:
![$$\begin{aligned} g\left( t \right) =\, & g_{b} + f_{1} \left[ {u_{1} \left( t \right)} \right] + \ldots + f_{K} \left[ {u_{K} \left( t \right)} \right] \\ =\, & g_{b} + f_{1} \left[ {p_{1} \left( t \right)*i\left( t \right)} \right] + \ldots + f_{K} \left[ {p_{K} \left( t \right)*i\left( t \right)} \right] \\ \end{aligned}$$](/wp-content/uploads/2017/04/A310669_1_En_1_Chapter_Equ12.gif)
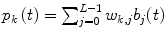 , and the PDM outputs u k are subsequently transformed by the respective polynomial nonlinearities f k (.) to produce the model-predicted blood glucose output (the asterisk denotes convolution) [30]:
, and the PDM outputs u k are subsequently transformed by the respective polynomial nonlinearities f k (.) to produce the model-predicted blood glucose output (the asterisk denotes convolution) [30]:![$$\begin{aligned} g\left( t \right) =\, & g_{b} + f_{1} \left[ {u_{1} \left( t \right)} \right] + \ldots + f_{K} \left[ {u_{K} \left( t \right)} \right] \\ =\, & g_{b} + f_{1} \left[ {p_{1} \left( t \right)*i\left( t \right)} \right] + \ldots + f_{K} \left[ {p_{K} \left( t \right)*i\left( t \right)} \right] \\ \end{aligned}$$](/wp-content/uploads/2017/04/A310669_1_En_1_Chapter_Equ12.gif)
(12)
Therefore, once an LVN model is trained based on input-output data, the PDMs and their associated nonlinearities can be readily obtained using the final (trained) values of the LVN parameters, i.e., weights w k,j , polynomial coefficients c n , k and Laguerre parameter α. For more details, the reader is referred to [32] (Chap. 2).
3 Comparison Between Compartmental and Volterra Models
3.1 Generalized Harmonic Balance Method
In order to examine the mathematical relationship between the aforementioned compartmental and Volterra models, we employ the generalized harmonic balance method to derive analytical relations between the two model forms, as outlined below for the second-order case of the nonparametric model [28]. This procedure can be extended to any order of interest.
By setting the input i(t) equal to 0, e st and 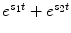 in the general Volterra model of Eq. (7) successively, the output g(t) becomes equal to k 0, k 0 + e st K 1(s) + e 2st K 2(s, s) + … and
in the general Volterra model of Eq. (7) successively, the output g(t) becomes equal to k 0, k 0 + e st K 1(s) + e 2st K 2(s, s) + … and 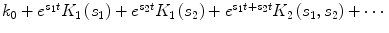 where K 1(s) and K 2(s 1, s 2) are the Laplace transforms of k 1(τ) and k 2(τ 1, τ 2) respectively. If we substitute these three input-output pairs into the differential equations of the compartmental models (Eqs. 1 and 2) for the open-loop model and (3–5) for the closed-loop model) and equate the coefficients of the resulting exponentials of the same kind, we can obtain analytical expressions for k 0, K 1(s) and K 2(s 1, s 2), in terms of the parameters of the respective compartmental model.
where K 1(s) and K 2(s 1, s 2) are the Laplace transforms of k 1(τ) and k 2(τ 1, τ 2) respectively. If we substitute these three input-output pairs into the differential equations of the compartmental models (Eqs. 1 and 2) for the open-loop model and (3–5) for the closed-loop model) and equate the coefficients of the resulting exponentials of the same kind, we can obtain analytical expressions for k 0, K 1(s) and K 2(s 1, s 2), in terms of the parameters of the respective compartmental model.
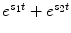 in the general Volterra model of Eq. (7) successively, the output g(t) becomes equal to k 0, k 0 + e st K 1(s) + e 2st K 2(s, s) + … and
in the general Volterra model of Eq. (7) successively, the output g(t) becomes equal to k 0, k 0 + e st K 1(s) + e 2st K 2(s, s) + … and 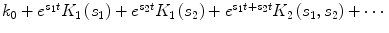 where K 1(s) and K 2(s 1, s 2) are the Laplace transforms of k 1(τ) and k 2(τ 1, τ 2) respectively. If we substitute these three input-output pairs into the differential equations of the compartmental models (Eqs. 1 and 2) for the open-loop model and (3–5) for the closed-loop model) and equate the coefficients of the resulting exponentials of the same kind, we can obtain analytical expressions for k 0, K 1(s) and K 2(s 1, s 2), in terms of the parameters of the respective compartmental model.
where K 1(s) and K 2(s 1, s 2) are the Laplace transforms of k 1(τ) and k 2(τ 1, τ 2) respectively. If we substitute these three input-output pairs into the differential equations of the compartmental models (Eqs. 1 and 2) for the open-loop model and (3–5) for the closed-loop model) and equate the coefficients of the resulting exponentials of the same kind, we can obtain analytical expressions for k 0, K 1(s) and K 2(s 1, s 2), in terms of the parameters of the respective compartmental model.To define the computational equivalence between the two model forms, we simulate the compartmental models with broadband input (insulin) data and we then estimate the kernels of the equivalent Volterra model, from the simulated input- output data. The accuracy of the estimated first and second-order Volterra kernels is assessed by comparison with the exact kernels of the equivalent Volterra model that is derived in analytical form from the differential equations of the compartmental models. The accuracy and robustness of the kernel estimates is evaluated under measurement noise conditions, in order to assess the performance of the Volterra approach.
3.2 Analytical Expressions of the Volterra Kernels of the Compartmental Model: Open-Loop Case
The bilinear term between insulin action and glucose concentration in Eq. (1) of the MM gives rise to an equivalent Volterra model of infinite order. However, for parameter values within the physiological range, a second-order Volterra model offers an adequate approximation for all practical purposes. Considering the insulin and glucose deviations from the respective basal values i(t) and g(t) as the input and the output respectively, we can derive analytically the Volterra kernels of the open-loop MM by applying the procedure outlined in Sect. 3.1 to the integro-differential equation:
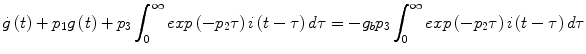
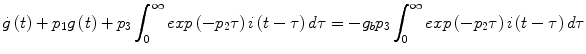
(13)
The above equation is derived from the MM by substituting the convolutional solution of Eq. (2):
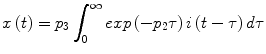
into Eq. (1). Upon application of this method, we derive the following analytical expressions in the Laplace domain for the first- and second-order Volterra kernels of the MM (k 0 = 0):
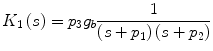
![$$K_{2}(s_{1}, s_{2}) = \frac{{p_{3}^{2} g_{b} }}{2}\frac{1}{{\left( {s_{1} + p_{1} } \right)\left( {s_{1} + p_{2} } \right)}}\,\frac{1}{{\left( {s_{2} + p_{1} } \right)\left( {s_{2} + p_{2} } \right)}}\left[ {1 + \frac{{p_{2} }}{{s_{1} + s_{2} + p_{1} }}} \right].$$](/wp-content/uploads/2017/04/A310669_1_En_1_Chapter_Equ16.gif)
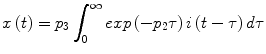
(14)
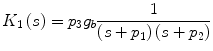
(15)
![$$K_{2}(s_{1}, s_{2}) = \frac{{p_{3}^{2} g_{b} }}{2}\frac{1}{{\left( {s_{1} + p_{1} } \right)\left( {s_{1} + p_{2} } \right)}}\,\frac{1}{{\left( {s_{2} + p_{1} } \right)\left( {s_{2} + p_{2} } \right)}}\left[ {1 + \frac{{p_{2} }}{{s_{1} + s_{2} + p_{1} }}} \right].$$](/wp-content/uploads/2017/04/A310669_1_En_1_Chapter_Equ16.gif)
(16)
The MM has, in principle, Volterra kernels of any order. However, it can be shown that the magnitude of the n-th order kernel is proportional to the n-th power of p 3 and, subsequently, an adequate Volterra model may only include the first two kernels (since the value of p 3 is on the order of 10−5–10−4). The resulting expressions for the first and second order kernels in the time domain are given in Eqs. (17) and (18) respectively:
![$$k_{1} \left( \tau \right) = - g_{b} \frac{{p_{3} }}{{p_{2} - p_{1} }}\left[ {\exp\left( { - p_{2}\tau_{1} } \right) - \exp\left( { - p_{2} \tau} \right)} \right]$$](/wp-content/uploads/2017/04/A310669_1_En_1_Chapter_Equ17.gif)
![$$\begin{aligned} k_{2}(\tau_{1},\tau_{2}) = & \frac{p_{3}^{2}g_{b}}{2(p_{2}-p_{1})^{2}} \biggl[[\exp(-p_{1}\tau_{1})-\exp(-p_{2}\tau_{1})][\exp(-p_{1}\tau_{2})-\exp(-p_{2}\tau_{2})] \nonumber \\ & + p_{2}\biggr[\biggr[\frac{1}{p_{1}}\exp[-p_{1}(\tau_{1}+\tau_{2})].[\exp(p_{1}\min(\tau_1,\tau_2)-1)]\biggr] \nonumber \\ & - \frac{1}{p_{2}}\exp[(-p_{1}\tau_{1}-p_{2}\tau_{2})+\exp(-p_{1}\tau_{2}-p_{2}\tau_{1})](\exp[p_2\min(\tau_1,\tau_2)]-1) \nonumber\\ & + \frac{\exp(-p_{2}(\tau_{1}-\tau_{2}))}{2p_2-p_1}(\exp[(2p_2-p_1)\min(\tau_1,\tau_2)]-1)\biggr]\biggr] \end{aligned}$$](/wp-content/uploads/2017/04/A310669_1_En_1_Chapter_Equ18.gif)
![$$k_{1} \left( \tau \right) = - g_{b} \frac{{p_{3} }}{{p_{2} - p_{1} }}\left[ {\exp\left( { - p_{2}\tau_{1} } \right) - \exp\left( { - p_{2} \tau} \right)} \right]$$](/wp-content/uploads/2017/04/A310669_1_En_1_Chapter_Equ17.gif)
(17)
![$$\begin{aligned} k_{2}(\tau_{1},\tau_{2}) = & \frac{p_{3}^{2}g_{b}}{2(p_{2}-p_{1})^{2}} \biggl[[\exp(-p_{1}\tau_{1})-\exp(-p_{2}\tau_{1})][\exp(-p_{1}\tau_{2})-\exp(-p_{2}\tau_{2})] \nonumber \\ & + p_{2}\biggr[\biggr[\frac{1}{p_{1}}\exp[-p_{1}(\tau_{1}+\tau_{2})].[\exp(p_{1}\min(\tau_1,\tau_2)-1)]\biggr] \nonumber \\ & - \frac{1}{p_{2}}\exp[(-p_{1}\tau_{1}-p_{2}\tau_{2})+\exp(-p_{1}\tau_{2}-p_{2}\tau_{1})](\exp[p_2\min(\tau_1,\tau_2)]-1) \nonumber\\ & + \frac{\exp(-p_{2}(\tau_{1}-\tau_{2}))}{2p_2-p_1}(\exp[(2p_2-p_1)\min(\tau_1,\tau_2)]-1)\biggr]\biggr] \end{aligned}$$](/wp-content/uploads/2017/04/A310669_1_En_1_Chapter_Equ18.gif)
(18)
These first and second-order Volterra kernels are plotted in Fig. 2 (top panel) for typical MM parameter values within the physiological range [25, 34]: g b = 80 mg/dl, p 1 = S G = 0.02 min−1, p 2 = 0.028 min−1 and p 3 = 10−4 min−2ml/μU, which yield S 1 = 0.0036 min−1/μU ml−1. Since the specific parameter values define the MM description of insulin-glucose dynamics, they also define the form of the equivalent Volterra kernels. The form of the first-order kernel in Fig. 2 (top left panel) indicates that an 10 μU/ml insulin concentration increase will cause a first-order drop in plasma glucose concentration that will reach a minimum of about −1.2 mg/dl about 36 min later, rising after that to half the drop in about 1 h and relaxing back to the basal value about 4 h after the minimum. The positive values of the second-order Volterra kernel indicate that the actual glucose drop caused by the insulin infusion will be slightly less than the first-order prediction (sublinear response). For instance, an insulin concentration increase of 100 μU/ml will not cause a maximum glucose drop of 12 mg/dl (as predicted by its equivalent first-order kernel) but a drop of about 10.5 mg/dl due to the antagonistic second-order kernel contribution.
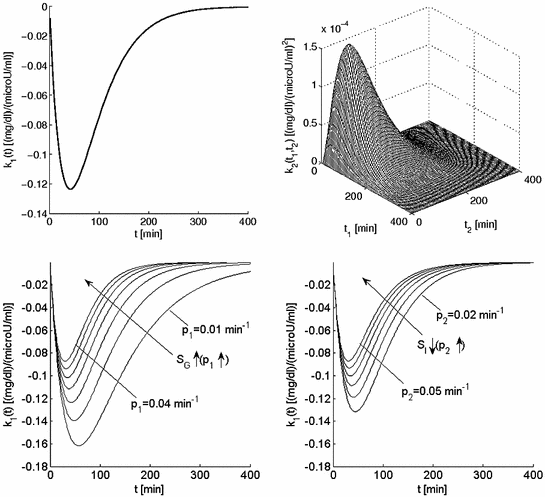

Fig. 2
Top panel The first-order (left) and second-order (right) Volterra kernels of the minimal model for typical values of its parameters within the physiological range (S G = 0.02 min−1 and S I = 0.0036 min−1/μU ml−1). Bottom panel Effect of the two key parameters p 1 and p 2 of the open-loop MM on the form of the equivalent first-order kernel. Note that the glucose effectiveness S G is equal to p 1 and the insulin sensitivity S I is inversely proportional to p 2 (and proportional to p 3 ). These plots offer a visual understanding of the effects of changes in these parameters (p 1 between 0.01 and 0.04 min−1, p 2 between 0.02 and 0.05 min−1) on the first-order insulin-glucose dynamics (see text)
Changes in these parameter values affect the form and the values of the kernels in the precise manner described by Eqs. (17) and (18). The effects of changes in the two MM parameters p 1 and p 2 on the equivalent first-order kernel are illustrated in Fig. 2 (bottom panels) for a range of physiological values (p 1 between 0.01 and 0.04 min−1 and p 2 between 0.02 and 0.05 min−1 [34], keeping p 3 = 10−4 min−2 ml/μU constant). Note that changes in p 3 simply scale the first-order kernel according to Eq. (17) and do not alter its form (proportional dependence)—nor do they alter the form of the second-order kernel (they scale it quadratically). A direct sense of the effects of parameter changes is obtained by the waveforms of Fig. 2: for instance, as p 1(S G ) increases, the maximum drop of the first-order kernel becomes smaller and its dynamics (i.e. the drop to the minimum and the return to basal value) become faster. Similar effects are observed when p 2 increases (or S I decreases).
3.3 Analytical Expressions of the Volterra Kernels of the Compartmental Model: Closed-Loop Case
To derive the analytical expressions of the kernels in the closed-loop case, we approximate the threshold function of Eq. (6) with a polynomial as indicated below, assuming that θ is equal to zero (i.e. insulin secretion is triggered when the glucose concentration rises above its basal value):
![$$\beta T_{h} \left[ {g\left( t \right)} \right] \approx \beta_{1} g\left( t \right) + \beta_{1} g^{2} \left( t \right) + \ldots$$](/wp-content/uploads/2017/04/A310669_1_En_1_Chapter_Equ19.gif)
where g(t) is the deviation of glucose plasma concentration from its basal value. Equation (19) provides an accurate representation of (6) within a desired dynamic range for glucose values g(t) (Weierstrass theorem), whereby the coefficients β i can be estimated in a mean-square sense. However, note that the subsequent analysis is valid for any values of these coefficients. Equation (5) can be rewritten as:
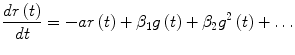
![$$\beta T_{h} \left[ {g\left( t \right)} \right] \approx \beta_{1} g\left( t \right) + \beta_{1} g^{2} \left( t \right) + \ldots$$](/wp-content/uploads/2017/04/A310669_1_En_1_Chapter_Equ19.gif)
(19)
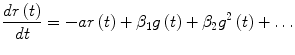
(20)
The solution of Eq. (20) is given by:
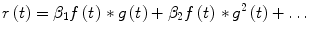
where the asterisk denotes convolution and f(t) = e −at u(t). Also, from Eq. (4) we have
![$$\frac{dx\left( t \right)}{dt} = - p_{3} h\left( t \right){ \,*\, }\left[ {i\left( t \right) + r\left( t \right)} \right]$$](/wp-content/uploads/2017/04/A310669_1_En_1_Chapter_Equ22.gif)
where 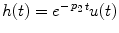 . Then, Eq. (3) becomes:
. Then, Eq. (3) becomes:
![$$\frac{dg\left( t \right)}{dt} + p_{1} g\left( t \right) = - p_{3} g\left( t \right)\left[ {h\left( t \right){ \,*\, }i\left( t \right) + \beta_{1} h\left( t \right){ \,*\, }f(t){ \,*\, }g\left( t \right) + \beta_{2} h\left( t \right){\, *\, }f(t){ \,*\, }g^{2} \left( t \right) + \ldots } \right].$$](/wp-content/uploads/2017/04/A310669_1_En_1_Chapter_Equ23.gif)
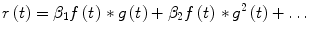
(21)
![$$\frac{dx\left( t \right)}{dt} = - p_{3} h\left( t \right){ \,*\, }\left[ {i\left( t \right) + r\left( t \right)} \right]$$](/wp-content/uploads/2017/04/A310669_1_En_1_Chapter_Equ22.gif)
(22)
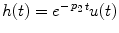 . Then, Eq. (3) becomes:
. Then, Eq. (3) becomes:![$$\frac{dg\left( t \right)}{dt} + p_{1} g\left( t \right) = - p_{3} g\left( t \right)\left[ {h\left( t \right){ \,*\, }i\left( t \right) + \beta_{1} h\left( t \right){ \,*\, }f(t){ \,*\, }g\left( t \right) + \beta_{2} h\left( t \right){\, *\, }f(t){ \,*\, }g^{2} \left( t \right) + \ldots } \right].$$](/wp-content/uploads/2017/04/A310669_1_En_1_Chapter_Equ23.gif)
(23)
The above equation can be used to obtain the equivalent Volterra kernels of the closed-loop model, following the procedure outlined before for the open-loop model. The resulting expressions for the first-order and the second-order kernels in the Laplace domain are given by Eqs. (24) and (25) respectively (k 0 = 0):
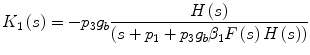
![$$\begin{aligned} K_{2} \left( {s_{1} ,s_{2} } \right) = & \; - p_{3} \left[ {\left( {\beta_{1} + \beta_{2} } \right)} \right]g_{b} \frac{{H\left( {s_{1} + s_{2} } \right)F\left( {s_{1} + s_{2} } \right)K_{1} \left( {s_{1} } \right)K_{1} \left( {s_{2} } \right)}}{{s_{1} + s_{2} + p_{1} + p_{3} g_{b} \beta_{1} H\left( {s_{1} + s_{2} } \right)F\left( {s_{1} + s_{2} } \right)}} \\ & + \;\frac{1}{2}\frac{{H\left( {s_{1} } \right)K_{1} \left( {s_{2} } \right)H\left( {s_{2} } \right)K_{1} \left( {s_{1} } \right)}}{{s_{1} + s_{2} + p_{1} + p_{3} g_{b} \beta_{1} H\left( {s_{1} + s_{2} } \right)F\left( {s_{1} + s_{2} } \right)}} \\ \end{aligned}$$](/wp-content/uploads/2017/04/A310669_1_En_1_Chapter_Equ25.gif)
where F(s), H(s) are the Laplace transforms of f(t), h(t) respectively, i.e. 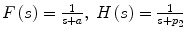 .
.
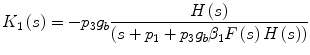
(24)
![$$\begin{aligned} K_{2} \left( {s_{1} ,s_{2} } \right) = & \; - p_{3} \left[ {\left( {\beta_{1} + \beta_{2} } \right)} \right]g_{b} \frac{{H\left( {s_{1} + s_{2} } \right)F\left( {s_{1} + s_{2} } \right)K_{1} \left( {s_{1} } \right)K_{1} \left( {s_{2} } \right)}}{{s_{1} + s_{2} + p_{1} + p_{3} g_{b} \beta_{1} H\left( {s_{1} + s_{2} } \right)F\left( {s_{1} + s_{2} } \right)}} \\ & + \;\frac{1}{2}\frac{{H\left( {s_{1} } \right)K_{1} \left( {s_{2} } \right)H\left( {s_{2} } \right)K_{1} \left( {s_{1} } \right)}}{{s_{1} + s_{2} + p_{1} + p_{3} g_{b} \beta_{1} H\left( {s_{1} + s_{2} } \right)F\left( {s_{1} + s_{2} } \right)}} \\ \end{aligned}$$](/wp-content/uploads/2017/04/A310669_1_En_1_Chapter_Equ25.gif)
(25)
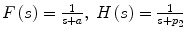 .
.Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree







