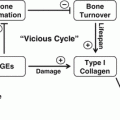
Fig. 9.1
The ability of bone to resist fracture depends on each level of organizational hierarchy from the triple helix of collagen being cross-linked (left) and filled with mineral crystals through arrangement of osteons or trabeculae to the shape (right)
Structural properties are derived from the cross-sectional geometry of cortical bone (the analog for trabecular bone is architectural properties) and include the moment of inertia (or second moment of area), endocortical circumference, periosteal circumference, bone cross-sectional area (cortex only), and total cross-sectional area (cortex and marrow space). They are related to one another; but from the perspective of engineering mechanics, moment of inertia and bone cross-sectional area characterize the ability of whole-bone to resist bending/torsion and compression/tension, respectively. Also, an increase in the periosteal circumference—for example, during growth—imparts a greater increase in the principal moment of inertia (I min or I max) than an increase in bone cross-sectional area (Ct.Ar). Given equivalent material properties, normal bone and diabetic bone would break at the same force when loaded in compression if there is no difference in Ct.Ar, but the same diabetic bone would break at a lower force when loaded in bending if the I min is less for the diabetic bone than for the normal bone (Fig. 9.2). That is, two different bones can have the same Ct.Ar but different values of I min or polar moment of inertia (J = (I min + I max)/2) in the case of torsion. Also, the moment of inertia varies with the orientation of the bone relative to the bending axis (Fig. 9.3). Therefore, the invariant calculations are often reported in the literature (I min corresponds to bending about the minor axis of the bone cross section or the minimum distance between centroid and the periosteal surface).
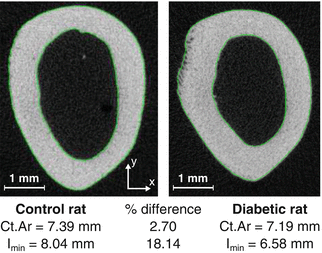
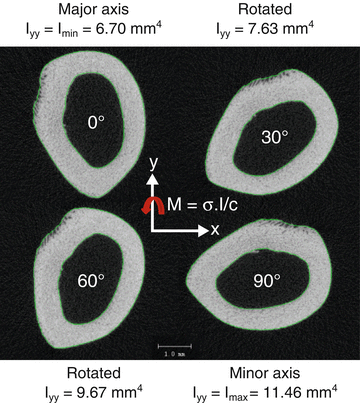

Fig. 9.2
The cross-sectional area (Ct.Ar) of a femur mid-shaft can be similar between two different rats, as an example, while the moment of inertia (I min) is considerably different. If the material properties are equivalent between the animals, then the strength in compression will be similar but weaker in bending for the diabetic than for the nondiabetic rat

Fig. 9.3
As a bone rotates with respect to the axis of bending, the moment of inertia changes. For a full rotation, there is maximum value and minimum value. In bending tests of rodent femurs to determine material properties, the minimum principal moment of inertia corresponds to bending about the medial-lateral axis
From human imaging studies, there is evidence that type 1 diabetes (T1D) affects bone structure in deleterious way [5], especially if glucose is poorly controlled or if T1D starts at a young age [6]. However, since most T1D patients are treated with insulin, bone structure can normalize with age [7] and structural indices of the hip do not necessarily differ between men (43.6 ± 5.1 years of age) with long-lasting T1D and those without diabetes [8]. For the most part, cortical bone structure of individuals with type 2 diabetes (T2D) does not significantly vary from that of age- and gender-matched nondiabetics as determined by various X-ray computed tomography (CT) scans [9–11], though there are reports of hip strength indices being adversely affected by T2D [12–14]. Additional information on bone structure can be found in Chap. 11.
The consequence of diabetes on size-dependent, structural strength is fairly well established for rodents (see reviews by Nyman [4] and Fajardo et al. [15]), but the mechanism of action is not particularly clear. Whether there is a loss of insulin production or an increase in insulin resistance in rodents, bones become structurally weaker and less rigid [16–19]. Of note though, diabetes develops before skeletal maturation in most rodent models of T2D, which can explain the discrepancy between rodent and human studies of bone structure involving T2D. Differences in bone structure between control mice and mice injected with streptozotocin (STZ), a toxin that decreases insulin production by the pancreas, explain the lower whole bone strength that occurs with the onset of T1D (Fig. 9.4) [19]. The primary cause for the reduction in bone size with diabetes is difficult to delineate in rodents as insulin, leptin, insulin-like growth factor-1 (IGF-1), and glucose levels cannot be independently controlled. Certainly, insulin and IGF-1 signaling are important to bone mass accrual [20, 21]. When the insulin receptor (IR) was conditionally deleted in cells of the osteoblast lineage (Osterix-cre), the femur mid-shafts of the mutant mice were strikingly narrow or slender and thus weaker than those from control littermates [22]. This effect was independent of body weight. Loss of insulin signaling however is likely not the only cause for deficits in diabetic bone structure. Rats with early onset T2D are hyperinsulinemic before 16 weeks of age, but yet, their bones have a much smaller moment of inertia than do the nondiabetic control rats before and after skeletal maturity [16] suggesting insulin resistance in osteoblasts or the action of other factors contribute to the deficit in cortical bone structure. Also, when human IRs were activated in the pancreas, liver, and brain of mice lacking IR in all cells including osteoblasts, there were no difference in bone properties between genotypes (euglycemic condition) [23]. These mutant mice are known to be hyperinsulinemic [24] and express more IGF-1 receptors in bone (insulin can bind IGF-1 receptors and vice versa) [23]. When a structural deficit in bone does occur with diabetes, it is likely the result of both a loss of anabolic action of insulin/IGF-1 on osteoblasts (especially in early-onset diabetes) and inhibition of bone formation by another mechanism (e.g., oxidative stress due to hyperglycemia).
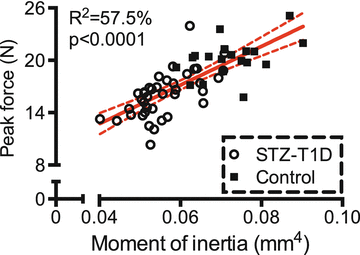

Fig. 9.4
In the streptozotocin (STZ) model of type 1 diabetes, a lower moment of inertia (structure) explains a significant portion of the lower bone strength in the diabetic mice compared to the age- and strain-matched controls
While poor bone structure (e.g., thinning of cortex) can lower areal bone mineral density (aBMD) as determined by dual-energy X-ray absorptiometry, the increase in fracture risk with T1D is disproportionate to the reduced aBMD [25]. Even though the elevated fracture risk is not as high for individuals with T2D, this increase also occurs independently of aBMD and bone structure [26–28]. Thus, diabetes must cause other changes to bone that lower fracture resistance. What follows is a tutorial on bone mechanics and review of studies reporting whether diabetes affects the material properties of bone.
Engineering Mechanics: Assessing Material Properties of Bone
Engineering materials (e.g., metal alloys, polymers, ceramics) break in many ways, and bone is no different. Intuitively, a bone fracture occurs when a region of the skeleton (e.g., femoral neck or distal radius) experiences a load that exceeds the maximum force that the bone region can sustain. Perhaps less obvious is that a healthy bone can yield (i.e., experience permanent damage) but not break. As long as that bone does not experience another high load too soon, remodeling removes the microdamage by replacing it with new tissue and returning the bone tissue to its normal material strength. In the case of unhealthy bone that cannot sustain damage after yielding, there is a “brittle” fracture. Through locomotion, bones—especially the femur, tibia, and spine—experience repetitive loads that are well below the yield force. Because there are numerous “flaws” in bone (e.g., lacunae, canaliculi, Haversian canals, Howship’s lacuna, and vacancies in the mineral) acting as stress risers, this cyclic loading at a low force causes microdamage formation over time. In the case of trabecular bone, microdamage accumulation from a bout of overloading [29] or fatigue loading [30] lowers the apparent-level strength. For either cortical or trabecular bone, the accumulation of microdamage eventually causes fatigue failure if allowed to proceed unchecked. Clinically, this leads to a stress fracture [31]. Such a bone stress injury has been postulated as a pathological mechanism of stage 0 diabetic Charcot foot [32].
Because materials can fail in a number of ways, such as an overload, insufficient energy dissipation, and fatigue, there are multiple engineering techniques to assess material properties. Comprehensive descriptions of these techniques can be found in several books on mechanical testing of bone or biomaterials [33–35]. Briefly, in all the techniques, force vs. displacement (f vs. d) data is recorded as a bone specimen is loaded to failure (i.e., stretched, compressed, twisted, or flexed). This is not the case for tests characterizing elastic or viscoelastic properties but is necessary to characterize post-yield behavior. After testing the specimen with an instrument that has a load cell (force) and an actuator (displacement), the f vs. d is processed in such way to remove specimen size (or structure) from the mechanical behavior. As a simple example, f vs. d from a monotonic, load-to-failure, tensile test of cortical bone is converted to engineering stress (σ) vs. engineering strain (ε) in which σ is f divided by the cross-sectional area of the specimen and ε is d divided by the original gage length of the extensometer, a device that clips to the specimen and records displacement between two knife edges (Fig. 9.5). The material properties are then determined from the resulting σ vs. ε curve (Fig. 9.5). Similar analysis occurs for bending tests (three point or four point) except that the equations to determine σ vs. ε differ as they are derived from beam theory and use the moment of inertia, instead of cross-sectional area of the specimen [36]. Also, in bending tests, displacement can be recorded from a deflectometer or the instrument’s linear variable displacement transducer that is part of the actuator.
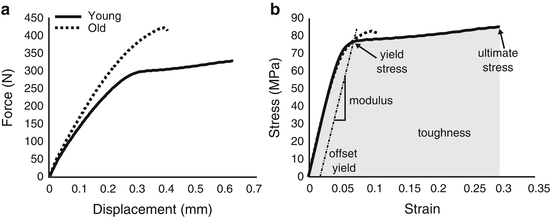

Fig. 9.5
Using the cross-sectional area of the specimen and gage length of the extensometer, the resulting force vs. displacement curve (a) from a tensile test is converted to an engineering stress vs. engineering strain curve (b) from which the material properties are determined. Determination of material properties are marked on curve for the bone specimen from a relatively young donor
With respect to fatigue testing, the primary outcome is fatigue life in which failure can be defined several ways: (1) actual numbers of cycles of loading experienced by the specimen before breaking (N f), (2) the number of cycles to reach a specified level of creep (permanent deformation or subsidence in the case of compressive testing) or a specified level of modulus loss, and (3) the steady-state creep rate (Fig. 9.6). Unlike most monotonic tests, fatigue tests are run in force control imparting a constant stress-amplitude (σ a = maximum σ minus the minimum σ during cyclic loading divided by 2). Although difficult in bone studies because the amount of material to generate replicates is limited, characterizing fatigue properties typically involves loading multiple sets of specimens at different stress amplitudes to generate a σ a vs. N f plot or S–N curve. Alternatively, σ a can vary across specimens to ensure that the initial maximum strain experienced by each specimen is constant (e.g., 4000 microstrain). Comparing results across fatigue studies is difficult because a number of extrinsic factors affect fatigue life (e.g., frequency of loading, waveform, initial strain, specimen geometry, loading mode, and the ratio of σ max to σ min).
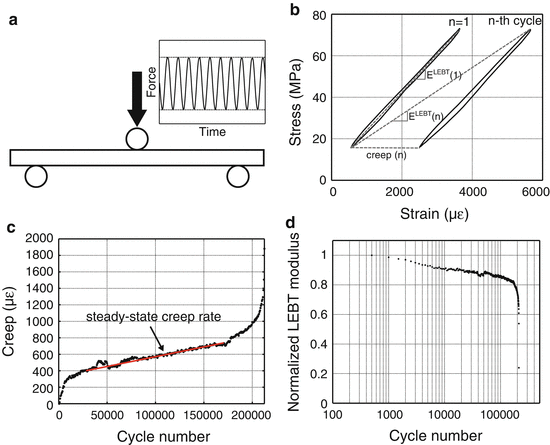

Fig. 9.6
In a fatigue test, the bone is dynamically loaded (sinusoidal wave profile) below the yield force (a). The force vs. displacement data is converted to stress vs. strain data to calculate changes in modulus, as determined by linear elastic beam theory (LEBT), and creep or permanent deformation (b). Creep occurs at a constant rate during most of the life of the specimen (c). As the number of cycles increases, the modulus decreases during fatigue (d)
Because fatigue testing does not delineate the ability of bone to resist microcrack initiation from its ability to resist microcrack propagation and accumulation, there is another type of material characterization technique known as fracture toughness testing. Involving a sharp notch that acts as the “worst flaw” in the material, a fracture toughness specimen can be loaded cyclically (fatigue crack growth resistance), monotonically (crack initiation toughness or total nonlinear strain energy release rate), or progressively (R-curve method to measure crack initiation and crack propagation toughness simultaneously).
Fracture toughness tests essentially characterize the ability of a material to resist fracture when a flaw is present. Engineers use this material property to determine what is the tolerable flaw size that a particular structure can have for a given service load without failing. There are acoustic devices to determine the size of flaws or cracks in structures such as airplane wings, but no such method is available for detecting microcracks in bone in vivo. Acoustic techniques such as ultrasound or acoustic emission are however being developed to monitor microdamage progression in in vitro tests [37, 38]. Traditionally, the assessment of microdamage morphology ex vivo involves bulk staining with a chelating agent and fluorescence microscopy [39] and more recently contrast-enhanced micro-CT (μCT) using an agent (e.g., barium sulfate) with higher X-ray attenuation than bone [40]. Such methods have been used to demonstrate associations between loading mode (compression, tension, torsion) and damage morphology (linear microcracks, diffuse damage) [41, 42]. To the best of our knowledge, differences in microdamage morphology between diabetic and otherwise normal bone has not been investigated.
Combining Material Properties with Bone Structure Using Finite Element Analysis
There is a way to incorporate the contributions of both structure and material to fracture resistance: apply the finite element method to the boundary value problem for a continuum body like bone. Two centuries after the first application of mechanics to bone by Galileo (1638), anatomists and engineers—Ward, Engel, von Meyer, and Culmann—connected the structure and architecture of bone to the stresses acting within bone [43]. While elegant graphical techniques matched bone structure/architecture to principal stress directions, the basis of Wolff’s law (1892), bone geometry is too complex for deriving analytical solutions using the theory of elasticity to determine the displacement response to prescribed boundary conditions. This was overcome in the 1960s for all complex structures when a numerical method was developed to solve the equilibrium, strain–displacement, and stress–strain equations comprising the boundary value problem in solid mechanics [44]. Since then, finite element analysis (FEA) has been the cornerstone of engineering design. Beginning in the 1990s, researchers in the field of orthopaedic biomechanics began developing three-dimensional finite element models of bone [45] and bone implants [46]. This became possible with the advent of quantitative CT (QCT) because voxels in the CT scan can be directly converted to elements that discretize the complex bone geometry into a mesh (Fig. 9.7) allowing for the creation of the linear algebra problem that is then solved in an iterative fashion by a finite element solver. Moreover, CT attenuation can be converted to material property definitions when incorporating a hydroxyapatite (HA) phantom into the scan.
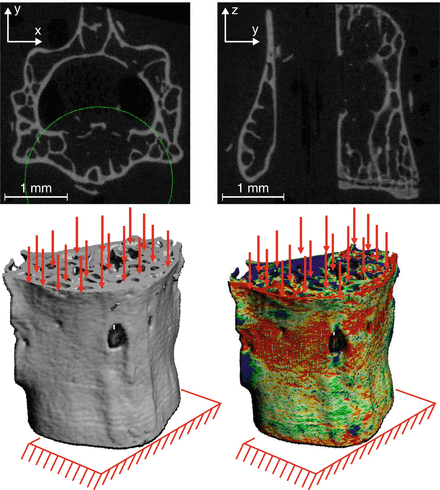

Fig. 9.7
A finite element model can be directly converted from the voxels of a micro-computed tomography scan of a bone. The finite element analysis calculates the strain distribution throughout the bone. In this example, the boundary conditions of the mouse lumbar vertebra simulate compression loading
With ample evidence that predictions of stiffness and strength by QCT-FEA strongly correlate with experimental measurements as determined by whole bone testing of cadaveric tissue, namely the proximal femur [45, 47, 48], distal radius [49, 50], and vertebra [51], the methodology has been applied to QCT scans of patients in clinical trials testing the efficacy of drugs to prevent fractures in mainly postmenopausal women (but also men in the MrOS cohort). For example, differences in predicted strength between placebo and therapy have been reported for alendronate (a bisphosphonate) [52, 53], combined teriparatide (recombinant parathyroid hormone 1–34) and alendronate [54], alendronate and then teriparatide [55], teriparatide to treat glucocorticoid-induced osteoporosis [56], odanacatib (cathepsin K inhibitor) [57, 58], denosumab (anti-RANKL antibody) [59], combined odanacatib and teriparatide [60], and combined teriparatide and denosumab [61]. An open question is how well these strength predictions explain the drug-related reduction in fracture incidence after adjusting for aBMD, which of course increases with treatment. QCT-FEAs are capable of fracture discrimination [52, 62–66], though some overlap in predicted strength exists between non-fracture and fracture cases [63, 67]. In a 5-year case–control study (>65 years of age) using baseline QCT scans of the spine and hip to develop the finite element model, the age-adjusted odds ratio for vertebral and hip strength predictions was significant for women and men [68]. That is, women and men with low vertebral strength or low hip strength, as predicted by QCT-FEA, were ~2 or ~4 times more likely, respectively, to suffer a fracture, and these odd ratios were still significant even if adjusted for most aBMD measurements.
To date, there is a paucity of studies investigating whether CT-derived FEA is useful for identifying diabetics who are at risk of a fracture (see Chap. 3). QCT-FEA or even high-resolution (HR)-peripheral CT (pCT)-FEA might not be particularly effective in the case of diabetes, unlike osteoporosis. The power of FEA is its ability to account for the structure in the response of a continuum body to loading or specifically boundary conditions, and as previously mentioned, diabetes does not necessarily affect bone structure. Moreover, the material properties must be defined in the FEA, and they are typically based on assumed empirical relationships between elastic modulus and bone density or strength and bone density acquired from mechanical testing of cadaveric tissue. There are no such relationships derived from diabetic bone. FEA calculates the stress–strain distribution throughout the bone as well as displacement for a given prescribed boundary condition (e.g., side-ways fall in which the trochanter is fixed against a rigid surface and the femoral head experiences a high joint reaction force). It does not actually calculate the strength of the bone. FEA predicted strength requires failure criteria (strain at which elasticity no longer holds), and yield strain or the damage tolerance of diabetic bone relative to normal bone is not yet known.
Age- and Diabetes-Related Changes in Material Properties of Bone
There is little known about the effect of T1D or T2D on the material properties of human bone or bone from nonhuman primates. This is likely to change in the coming years, as there is a growing recognition for the need to understand how diabetes is increasing fracture risk. The challenge to the assessment of material properties is the procurement of bone samples that can be machined into the proper test geometry. Traditionally, this is done using cadaveric bone, but information about whether the donor had diabetes and for how long is rarely provided by willed body programs and tissue allograft banks. Alternatively, bone biopsies from surgeries or from the iliac crest can be analyzed by other techniques such as μCT, Raman spectroscopy, Fourier transform infrared spectroscopy, high performance liquid chromatography, and quantitative back-scatter electron microscopy [69] to identify organizational and compositional differences between diabetic and nondiabetic bone. Such information would inform as to whether diabetes affects bone quality. In on-going work, trabecular bone biopsies are being collected from patients undergoing total hip arthroplasty (osteoarthritis, not hip fracture), and those with glycated hemoglobin levels (HbA1c) greater than six tend to have bone with lower apparent strength and higher AGEs [70].
To the best of our knowledge, there are only three studies that reported material properties of human bone from donors with diabetes. In the earliest study (1998), metatarsals were acquired from amputations (30 diabetics and 19 nondiabetics) performed for a variety of reasons (elective, trauma, infection, tumor) [71]. The type of diabetes was not specified nor the duration. An additional set of metatarsals was acquired from 29 cadavers. Tested in the three-point bending, the estimated modulus and strength of the diaphysis (cortical bone) did not differ between the two groups. However, there was an age discrepancy in which the diabetics were 51.3 ± 8 years of age and the normal controls were 72.4 ± 10 years of age, suggesting the effect of diabetes on bone material properties is similar to the effect of aging. In a follow-up study by the same group (2006), beam specimens (nominal dimensions of 30 × 4 × 2 mm) were extracted from the anterior aspect of tibia, which were acquired from amputations (seven diabetics and seven nondiabetics) [72]. Again, there were no differences in the material properties (modulus, strength, and fracture toughness) between the younger diabetic bone and the elderly nondiabetic bone. While an extended period of non-ambulation (unspecified) was part of the exclusion criteria, confounding factors related to the amputation limit the interpretation of these findings. Nonetheless, the idea that diabetes is a form of accelerated aging with respect to material properties of bone is intriguing. In the third study, the fracture toughness of cadaveric bone from one donor with diabetes (duration not specified) was 40 % lower than cadaveric bone from several donors without diabetes [73].
Given the dearth of information about how diabetes affects the material properties of human bone, we turn to the literature reporting how material properties of cadaveric bone change with age. Evidence that the material properties of human cortical bone changed with age began to appear in the literature around the time that the finite element method was being developed [74–76]. However, there were several studies that did not find age-related changes in tensile strength [77, 78] owing to discrepancies in sample size (sometimes less than ten) and storage conditions (frozen vs. fixed). Then, testing 175 tensile specimens from 33 cadaveric femurs acquired from donors spanning 20–89 years of age, Burstein et al. showed that yield and ultimate stress (i.e., material strength) significantly decreased 2.2 % per decade and that energy dissipation (i.e., toughness) significantly decreased by 6.8 % per decade (Fig. 9.8) [79].
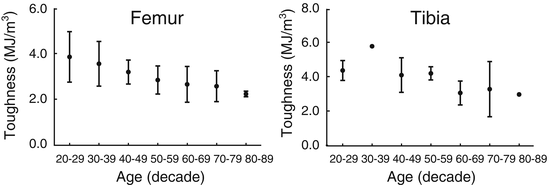

Fig. 9.8
The toughness of human cortical bone decreases over life-span (adapted from Burstein et al. [79])
Age-related decrease in material strength of cortical bone has since been reported by a number of independent groups [80–83], though there is variance in the relationship between strength and age (some elderly donors have strong bones). Material strength can be measured as the stress at yielding when permanent damage begins to form or as the peak stress endured by bone during failure. A primary determinant of this decrease in material strength is an age-related decrease in apparent bone density (wet mass divided by the specimen volume or radiation absorption), but it is not the sole determinant [80] as the rate of decrease in strength is greater than that of density [81]. Of course, apparent bone density is product of intracortical porosity and degree of mineralization (or ash fraction). Both characteristics inversely or directly correlate, respectively, with strength [84, 85]. Therefore, if diabetes causes an increase in porosity or decrease in mineralization, then it would decrease the material strength of bone, thereby increasing fracture risk.
Collagen cross-links via lysyl oxidase are another important determinant of bone strength. When female rats were administered the toxin β-amino-propionitrile (BAPN) to inhibit lysyl oxidase, there was a decrease in material strength of bone that accompanied a decrease in mature enzymatic collagen cross-links (pyridinolines) without affecting mineral density [86]. Recently, treatment of growing male mice with BAPN resulted in reduced cortical bone strength, reduced fracture toughness, and reduced mature-to-immature cross-link ratio (these properties were positively correlated) without affecting tissue mineral density as determined by μCT [87]. Diabetes could potentially alter enzymatic collagen cross-linking. The B6 vitamer known as pyridoxamine is a cofactor of lysly oxidase, and diabetes via an oxidative stress pathway could potentially decrease enzymatic activity. There is at least one study reporting a decrease in pyridoxamine and enzymatic collagen cross-links with the progression of T2D in the WBN/Kob rat (material properties of bone were not directly reported) [88]. More information on the contribution of collagen cross-link to bone strength can be found in several review articles [89–91].
With aging, both advanced glycation end products (AGEs) [92, 93] and microdamage [94–98] increase in bone despite continual turnover throughout life. Fatigue loading of cortical bone in vitro to generate microdamage reduces material strength [99, 100]. Conceivably, diabetes alters the matrix of bone in way that favors damage accumulation, especially if remodeling is impaired (turnover marker are generally down in diabetics).
As is the case with material strength, several independent groups have reported that toughness decreases with age [82, 83, 93]. In general, the collagen phase is primarily responsible for bone toughness or the ability of bone to dissipate energy during failure. Much of this energy occurs after yielding such that “brittle” bone has very low post-yield toughness. There are a number of collagen characteristics that partially explain the age-related decrease in human bone toughness: increase in porosity (i.e., loss of collagen) [82], decrease in collagen strength [92], a decrease in isometric shrinkage temperature or the peak rate of contraction of the collagen (i.e., collagen integrity) [101], an increase in secondary osteonal area [96], a decrease in collagen content relative to dry mass of bone [93], an increase in pentosidine [93], and a decrease in bound water [102, 103]. As such, the hyperglycemia that occurs with diabetes can possibly cause bone to become brittle through modifications to the collagen phase. For example, the accumulation of AGEs like pentosidine over the duration of diabetes could decrease the ability of collagen to deform and slide relative to the mineral phase, thereby decreasing toughness (for a review of bone quality in diabetes, see [104]).
The evidence for this possible mechanism of AGE accumulation reducing bone toughness comes from the documented association between pentosidine or AGEs and bone toughness [92] or fracture toughness [105] and in vitro riboslyation experiments [106]. When bovine cortical bone (18–24 months old) was incubated in high concentrations of sugar, namely 0.6 M ribose, for 14 or 38 days to induce nonenzymatic cross-linking, there was a reduction in fracture properties related to post-yield energy dissipation mechanisms, not strength [106, 107]. However, when fetal bovine bone was incubated in 0.2 M ribose for 15 days, there were no differences in material properties, as determined by three-point bending tests, between control and ribosylated bone, despite ribose significantly increasing pentosidine [108]. This suggests that sugar concentration and mineralization status of the tissue influence whether inducing AGEs lowers the material properties of bone. With respect to trabecular bone, which is likely more susceptible to nonenzymatic, glycation-mediated collagen cross-linking than cortical bone [109, 110], in vitro incubation in 0.6 M ribose for 7 days has been reported to lower the difference between strain at maximum stress and strain at yielding (post-yield energy) as determined by compression tests of human trabecular bone [111, 112]. Adding an AGE blocker such as aminoguanidine [108] or n-phenacylthiazolium bromide [112] partially prevents ribose-induced AGEs. However, in vivo demonstration that inhibiting diabetes-related increase in AGE prevents a loss of bone toughness has yet to be demonstrated.
As previously mentioned, there are multiple ways to characterize the fracture toughness of human cortical bone. Whether determined as the critical stress state beyond which the crack begins to grow (stress intensity factor K), the nonlinear elastic strain energy dissipated prior to and during fracture (J-integral), or the toughness evolution with crack extension (crack resistance curve or R-curve), fracture toughness of human bone decreases with advancing age [73, 83, 92, 113, 114]. Moreover, there are many factors that correlate with fracture toughness of human cortical bone: apparent bone density [115], porosity [96, 116], collagen integrity [101], microdamage [96, 117], bound water [118], and pentosidine [92, 105]. Diabetes could potentially lower fracture toughness and overall fatigue resistance by increasing intracortical porosity and increasing AGEs such that the matrix has less capacity to resist damage.
Differences in Material Properties of Bone Between Nondiabetic and Diabetic Rodents
Different strains of rodents have been used to study the effects of both T1D and T2D on the material properties of the bone, although there are more studies reporting diabetes-related differences in structural properties such as stiffness and peak force [4]. Rodent models of T1D involve impairing pancreatic or β cell function [119]. This can be achieved by injecting a toxin such as alloxan or STZ, infecting transgenic mice with a virus specifically designed to disrupt β cells, and breeding mice that cannot adequately produce insulin (the non-obese diabetic or NOD mouse) [120]. Type 2 diabetic models involve single gene or polygenic mutations [15, 119, 121]. Rodents with single gene mutations become spontaneously diabetic. Examples include mutations in the leptin gene (db/db mouse or ZDF rat), the leptin receptor (ob/ob mouse), and in the IGF-1 receptor gene of muscle cells (MKR mouse). Note that the loss of function in these genes may affect the skeletal phenotype in ways that are independent of diabetic effects. Diabetes in polygenic models of T2D can also spontaneous, but it typically involves diets with moderate to high fat, thereby enuring that frank diabetes occurs. These models vary in the severity of diabetes, and age of diabetic onset often occurs before skeletal maturity. As such, more preclinical and clinical studies are needed to determine which rodents models best represent how diabetes affects bone in humans.
In general, material strength and toughness of bone are lower for rodents with T1D than without diabetes [18, 19, 122–126]. Table 9.1 summarizes some recent studies reporting material properties of bone in primarily STZ-induced models of T1D. Non-fasting glucose levels reproducibly exceed 350 mg/dL in this model with normal levels being less than 100 mg/dL (severity depends on strain of mouse however). There is a lack of information on the material properties of bone in other non-toxin models such as the NOD mouse. Difference in bone toughness between T1D rodents and nondiabetic controls depends on the duration of diabetes [19, 126], which could explain why not all T1D studies report a difference in this material property [18, 123].
Table 9.1
Summary of the recent literature reporting differences in material properties of bone between normal rodents and rodents with type 1 diabetes
Strain of rodent | Age when diabetes started (weeks) | Duration of diabetes (weeks) | Bone tested in bending | Material strength (%) | Toughness (%) | Comments on toughness assessment | Reference |
|---|---|---|---|---|---|---|---|
SDa rat | 10 | 7 | Femur | NRb | −34 | Work-to-failure inthe plasticrange(n = 12 pergroup) | [122] |
Tibia | −40 | ||||||
F344 rat | 12 | 12 | Ulna | −7.8 | −19 (NS) | Work-to-failurec(n = 9–12 per group) | [18] |
Ulna | −1.6 (NS) | −33 | |||||
SD rat | 12 | 12 | Femur | NR | +2.6 (NS) | ||
Femur | NR | −26 (NS) | |||||
Wistar ratd | 10 | 6 | Femur | −5.9 (NS) | −8.9 (NS) | Area under the stressvs. straincurve(n = 16 pergroup) | [126] |
12 | −5.9 (NS) | −17.1 (NS) | |||||
Wistar rat | 13 | 8 | Femure | −36.7 | −58.1 | Area under the stressvs. strain curve (n = 7 per group) | [124] |
BALB/c mouse | 14 | 5.7 | Femur | −3 | NR | Femur cross section assumed to be an ellipsoid (n = 5–9 per group) | [123] |
CD-1 mouse | 10 | 5 | Femur | −16.8 | 6 (NS) | Post-yield deflection (n = 7–9 per group) | [125] |
DBA/2 J mouse | 11 | 10 | Femur | −0.2 (NS) | −11.9 (NS) | Post-yield toughnessf (n = 6–11 per group) | [19] |
15 | −9.2 | −33.4 (NS) | |||||
18 | −10.8 | −57.9 |
As previously mentioned, a recent review by Fajardo et al. [15] comprehensively summarizes the skeletal phenotype of multiple rodent models of T2D. With respect to material properties of bone, material strength and toughness are typically lower, on average, for rodents with diabetes than for the nondiabetic controls [16, 127–129], but the differences are not always statistically significant (Table 9.2). In the study by Hill-Gallant et al. [129], there was a difference in the estimated compressive strength of cancellous bone (femur metaphysis), but no significant differences in material strength were observed for the femoral mid-shaft when subjected to three-point bending. Using an indentation technique (described in the next section) to assess tissue properties, Hammond et al. [130] reported that the cortical tissue of the tibia mid-shaft from diabetic ZDSD rats had a higher resistance to indentation than the cortical tissue from nondiabetic CD rats, whereas Gallant et al. [131] reported the opposite effect of diabetes on indentation resistance when indenting the femur mid-shaft from similar CD and ZDSD rats. Besides the bone that was tested, the maximum indenting force differed between the studies (5 N vs. 10 N). Also, the rats became diabetic on a high fat diet at approximately 20 weeks of age, but the special diet was only given for 1 week in Hammond et al. study and for entire 12 weeks of diabetes in the Gallant et al. study. In a mouse model of juvenile T2D, Devlin et al. [132] performed a similar indentation test on tibia mid-shafts from 17-week-old, nondiabetic mice (SWR/J strain) and age-matched diabetic mice (TallyHo/JngJ) but using a maximum target force of 2 N (average of three sites). There was lower resistance to indentation with diabetes though method of indentation resistance was not exactly the same as the aforementioned studies. Note that in these indentation studies, the control animals are not littermates to the diabetic animals. Overall, there is a need for more biomechanical studies with sufficient sample size to establish the effect of diabetes on the material- and tissue-level properties of bone. Of the multiple models of T2D, the bone phenotype has only been reported for the Zucker Diabetic Fatty (ZDF), Zucker Diabetic Sprague Dawley (ZDSD), and WBN/Kob rats (Table 9.2).
Table 9.2
Summary of the recent literature reporting differences in material properties of bone between normal rodents and rodents with type 2 diabetes
Strain of rodent | Age when diabetes started (weeks) | Duration of diabetes (weeks) | Bone tested in bending
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
 Get Clinical Tree app for offline access
Get Clinical Tree app for offline access

|
|---|