Intensity-Modulated Radiation Treatment Techniques and Clinical Applications

K.S. Clifford Chao, Radhe Mohan, Timothy D. Marinetti, and Lei Dong

The previous edition of this chapter included literature reports through 2006. At that time intensity-modulated radiation therapy (IMRT) was still something of a novelty; 5 years later it is safe to say that the technique has become the de facto standard practice for many tumors. IMRT’s coming of age is described in thorough terms in the 2010 International Commission on Radiation Units (ICRU) report (hereafter ICRU 83), which spans 106 pages with over 350 references.¹ Readers new to the field will find this report an excellent synthetic introduction to IMRT; experienced practitioners should also note that it contains new reporting guidelines for clinical treatments.

The use of ionizing radiation for diagnosis and treatment goes back over a century; for a wonderfully concise review see Bernier et al.² An enduring clinical problem has been to achieve high levels of irradiation at the tumor site without causing extremely toxic or even fatal consequences in normal tissues in the path of the treatment beam. Advances in technology—especially fast, affordable computers—opened the prospect of true three-dimensional (3D) tailoring of radiation fluence with equipment and a planning timescale usable in the clinic. Since its introduction into clinical use,^3–4,5 IMRT has generated widespread interest. IMRT optimally assigns nonuniform intensities (i.e., weights) to tiny subdivisions of beams, which have been called rays or “beamlets.” The ability to optimally manipulate the intensities of individual rays within each beam permits greatly increased control over the radiation fluence, enabling custom design of optimum dose distributions. These improved dose distributions potentially may lead to improved tumor control and reduced normal tissue toxicity. For example, tumors of the head and neck often require concave-shaped treatment volumes to spare closely adjacent sensitive critical structures (e.g., brainstem, spinal cord). Such fluence distributions are easily done with IMRT but may be difficult or impossible by other techniques, including three-dimensional conformal radiation therapy (3DCRT). This is illustrated in Figure 10.1, which is taken from ICRU 83.

IMRT requires setting the relative intensities of tens of thousands of rays which make up an intensity-modulated treatment plan. This task cannot be accomplished manually and requires the use of specialized computer-aided optimization methods. The optimum beamlet intensities are determined using a systematic iterative process during which the computer sequentially generates intensity-modulated plans one by one, evaluates each of them according to user-selected criteria (“desired objectives”), and makes incremental changes in the ray intensities based on the deviation from the desired objectives. The quality of an intensity-modulated treatment plan produced in this manner depends on a number of factors. These include the mathematical function and parameters used by the optimization process to evaluate and compare competing treatment plans; the mathematics and algorithms of optimization; the number, orientation, and energy of radiation beams; margins assigned to the planning target volume (PTV) and to normal structures; dose-calculation algorithms; and so on. We will discuss many of these in this chapter.

The 2010 ICRU 83 report has some important conceptual changes. The previous ICRU reports for photon therapy (No. 50 in 1993 and its supplement, No. 62, in 1999) defined a reference point within the treatment volume, one that was easily located with anatomic landmarks and where dosage could be accurately measured. The prescription dose was something of an ideal to be sought. However, with IMRT, treatment volumes are more relevant, and doses are given and bounds set within those volumes. Also, the prescription dose itself is now taken to be the final result of treatment planning by the physicists and radiation oncologists. With literally thousands of degrees of freedom available to the planner, the dosage to a single point is no longer adequate to describe or evaluate a plan.

ICRU 83 cites the increase in the clinical impact and use of IMRT in the recent past: “In a survey performed in 2003 in the USA, among 168 radiation oncologists randomly selected, one-third was using IMRT. In 2005, a similar survey showed that more than two-thirds of radiation oncologists were using some form of IMRT, mainly for increased normal-tissue sparing or target-dose escalation”.^1,6,7 Another noteworthy metric is the number of research reports in the peer-reviewed literature concerning IMRT. A scan of the Web of Science database showed full papers with IMRT in the title as numbering <50 per year through 2001. It reached 100 in 2005 and has plateaued at about 140 for the years 2009–2011. One presumes the flattening of the publication rate has more to do with the fiscal woes plaguing the industrial countries since 2008 than a loss of interest in IMRT.

FIGURE 10.1. Comparison of conformal radiation therapy (CRT) (left) and intensity-modulated radiation therapy (IMRT) (right). The ability for CRT to alter isodose lines was limited to shaping of field boundaries with multileaf collimators (MLCs) or blocks, the use of wedges or compensators for missing tissues, and the use of central blocks for shielding critical structures. The IMRT beams can have highly nonuniform beam intensities (fluences) and are capable of producing a more concave-shaped absorbed-dose distribution. With neither conformal therapy nor IMRT can the planning organ at risk volume (PRV) always be completely avoided, but with IMRT the concave isodose curve that includes the planning target volume (PTV) better avoids the PRV. The black region indicates the PTV, the gray region indicates a PRV, and the line surrounding the PTV is a typical isodose contour. (Reprinted from ICRU Report 83: prescribing, recording, and reporting photon-beam intensity-modulated radiation therapy [IMRT]. J ICRU 2010;10[1]:1–106, with permission.)

IMRT RATIONALE

The term IMRT is used to mean much more than its literal meaning might suggest. Strictly speaking, the use of wedges and conventional compensators for surface curvature is also intensity modulation. In this chapter, IMRT is a form of 3DCRT in which a computer-aided optimization process is used to determine customized nonuniform fluence distributions to attain certain specified dosimetric and clinical objectives.

Viewed in this light, IMRT is intimately tied to 3D imaging. As ICRU 83 states: “Three-dimensional CRT, in general, and IMRT, in particular, increase the need for accurate anatomic delineation. This requires an adequate specification of the tumor location and a thorough knowledge of the processes of likely infiltration and spread”.¹

IMRT has many potential advantages. It can be used to produce dose distributions that are far more conformal than those possible with standard 3DCRT. Dose distributions within the PTV, in theory, can be made more homogeneous, and, if so desired, a sharper fall-off of dose at the PTV boundary can be achieved. Experience with current IMRT systems has led to an impression among many that IMRT inherently produces inhomogeneous dose distribution within the target volume. Inhomogeneity commonly observed is the result of the overriding need to partially or wholly protect one or more critical organs. In other words, the dose distributions tend to be more heterogeneous because the homogeneity criterion is made less important than the normal structure avoidance criterion. If all things were equal, the IMRT plan always should produce more homogeneous dose distribution than a plan made with uniform beams. A sharper fall-off of dose at the PTV boundary, in turn, means that the volume of normal tissues exposed to high doses may be reduced significantly. These factors may allow escalation of tumor dose, reduction of normal tissue dose, or both, hopefully leading to an improved outcome, including lower morbidity. A lower rate of complications also may mean lower cost of patient care following the treatment. In addition, IMRT has the potential to be more efficient with regard to treatment planning and delivery than standard 3DCRT, although gains in this direction are being realized rather slowly. The treatment design process is relatively insensitive to the choice of planning parameters, such as beam direction.^8–10 There are no secondary field-shaping devices other than the computer-controlled multileaf collimator (MLC). Furthermore, large fields and boosts can be integrated into a single treatment plan, and, in many cases, electrons can be dispensed with, permitting the use of the same integrated boost plan for the entire course of treatment.^11,12 An integrated boost treatment may offer an additional radiobiologic advantage¹³ in terms of lower dose per fraction to normal tissues while delivering higher dose per fraction to the target volume. Higher dose per fraction also reduces the number of fractions and hence lowers the cost and burden to the patient for a treatment course. IMRT also offers the potential of adaptive therapy—revision of the treatment plan according to imaging of tumor reduction and organ movement during the course of radiation therapy. Mechalakos et al. present a case study where weekly cone beam computed tomography (CBCT) was used to track treatment of a recurrent neck mass from a nasopharyngeal cancer.¹⁴

IMRT Limitations and Risks

We should recognize, however, that IMRT has limitations. There are many dose distributions (or dose–volume combinations) that are simply not physically achievable. Furthermore, our knowledge about what is clinically optimal and achievable and how best to define clinical and dosimetric objectives of IMRT is often limited. Moreover, the best solution may elude us because of the limitations of the mathematical formalism used or because of the practical limits of computer speed and the time required for finding it.

Uncertainties of various types (e.g., those related to daily, or interfraction, positioning; displacement and distortions of internal anatomy; intrafraction motion; and changes in physical and radiobiologic characteristics of tumors and normal tissues during the course of treatment) may limit the applicability and efficacy of IMRT. Dosimetry characteristics of a delivery device, such as radiation scattering and transmission through the MLC leaves, introduce some limitations in the accuracy and deliverability of IMRT fluence distributions. In addition, the limited spatial and temporal coverage and overall accuracy of current IMRT dosimetric verification systems, based principally on radiographic and radiochromic film, diminish the confidence in the delivered dose. Furthermore, most current dose-calculation models are limited in their accuracy, especially for the small, complex shapes required for IMRT. It is quite conceivable that inaccuracies in dose calculations may yield a solution different from the one derived if dose calculations were accurate. However, the most important factor that may limit the immediate success of IMRT is the inadequacy of imaging technology to define the true extent of the tumor, its extensions, and radiobiologic characteristics as well as geometric, dose-response, and functional characteristics of normal tissues.

We also should be aware of the risks of IMRT. The effect of large fraction sizes used in integral boost IMRT on tissues embedded within the gross tumor volume is uncertain and may present an increased risk of injury.¹⁵ There also may be an increased risk that improper use of spatial margins, coupled with the high degree of conformality with IMRT, may lead to geographic misses of the disease and recurrences, especially for disease sites where positioning and motion uncertainties play a large role or where there are significant changes in anatomy and radiobiology during the course of radiotherapy. Similarly, high doses in close proximity to normal critical structures may pose a greater risk of normal tissue injury. In addition, IMRT dose distributions are unusual and highly complex, and existing experience is too limited to interpret them properly and evaluate their efficacy. Finally, while IMRT can spare specific tissues compared to conventional radiation therapy, the use of many more beams and irradiation angles means that a larger volume of normal tissue is being exposed, albeit at lower accumulated doses. This may lead to unforeseen sequelae.

IMRT—An Unconventional Paradigm

The application, process, and dose distributions of IMRT are significantly different from those of conventional two-dimensional (2D) CRT or 3DCRT. This means the traditional methods of specification and fractionation of treatments, evaluation of treatment plans, and reporting of results are limited and new methods need to be introduced.

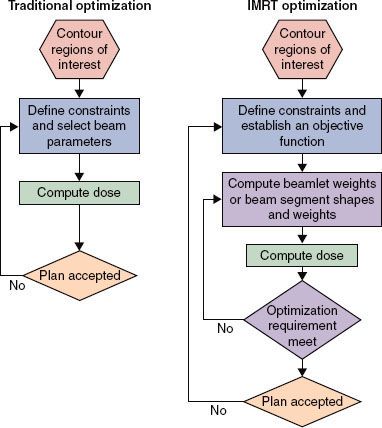
The traditional 3DCRT process involves “forward planning,” in which beam parameters (directions, apertures and their margins, beam weights, beam modifiers) are specified and dose distributions are computed. The treatment plan is evaluated by a human being, and, if necessary, beam parameters are modified to achieve a satisfactory dose distribution. In IMRT, an inverse process (“inverse planning”) is used in which the desired dosimetric and clinical objectives are stated mathematically (in the form of an “objective function”).^9,16–18 The term inverse planning should not be confused with the mathematical operation of matrix inversion. In the present context the word inverse is used to distinguish it from forward planning for conventional 3DCRT. As ICRU 83 concisely notes:

The inverse-planning process works iteratively to determine beam shapes and fluence patterns to achieve an optimal or acceptable absorbed-dose distribution. The IMRT optimization software iteratively adjusts beam parameters with the aim of obtaining the best possible approximation of the desired dose distribution. In each optimization iteration, the optimization software computes the value of the objective function (i.e., the IMRT plan score) to judge the overall quality of each of a large number of plans to choose the optimum one. However, it must be kept in mind that limitations of planning time may preclude full exploration of all the degrees of freedom (there can be many thousands), so whether the optimization is done by a variant of gradient or stochastic methods, the computed solution may not be the true global one. Final review by the radiation oncologist of any plan, of course, is required.

IMRT is most conformal and most efficient when all target volumes (gross disease, subclinical extensions, and electively treated nodes) are treated simultaneously using different fraction sizes. Such a treatment strategy has been called the simultaneous integrated boost.^15,19 This is in contrast to conventional radiotherapy in which the same fraction size (typically 1.8 or 2 Gy) is used for all target volumes with successive reductions in field sizes to protect critical normal structures and to limit the dose to electively treated and subclinical disease regions.

Alternative IMRT Approaches

During the past 15 years, a variety of techniques have been explored for designing and delivering optimized IMRT.^{4,5,8,15,20–49} Many of these are implemented in commercial IMRT systems. The most significant differences among the various approaches are in terms of the mechanisms they use for the delivery of nonuniform fluences. Although the merits of each often are speculated, the superiority of any of the approaches is difficult to assess because there have been no systematic comparisons of clinical treatment plans.

Of the various approaches proposed, two dominant but significantly different methods have emerged. Mackie et al.³⁴ proposed an approach called tomotherapy in which intensity-modulated photon therapy is delivered using a rotating slit beam. A temporally modulated slit MLC is used to rapidly move leaves in or out of the slit. Like a CT unit, the radiation source and the collimator continuously revolve around the patient. The patient is translated either stepwise between successive rotations (serial tomotherapy) or continuously during rotation (helical tomotherapy). For helical tomotherapy, the system looks like a conventional CT scanner and includes a megavoltage portal detector to provide for the tomographic reconstruction of the delivered dose distribution.

A commercial slit collimator (called MIMiC) of the type proposed by Mackie et al.³⁴ has been designed and built by the NOMOS Corporation (North American Scientific, Chatsworth, CA). It has been incorporated into the company’s serial tomotherapy system, known as Peacock, for planning and rotational delivery of intensity-modulated treatments.^26,27 Figure 10.2 shows an original “binary” collimator built by NOMOS and as mounted on a linac. The figure also shows a modern tomotherapy machine.

In the second approach, implemented first into clinical use at Memorial Sloan-Kettering Cancer Center,^{4,5,35,37,44,45,50} a standard MLC is used to deliver the optimized fluence distribution in either dynamic mode (defined as the leaves moving while the radiation is on) or static mode (i.e., “step-and-shoot” mode, defined as sequential delivery of radiation subportals that combine to deliver the desired fluence distribution), to deliver a set of intensity-modulated fields incident from fixed-gantry angles (see Fig. 10.3). These techniques are gaining wide acceptance rapidly. Every major commercial treatment-planning system manufacturer has implemented one or both of these.

A third approach, called intensity-modulated arc therapy or IMAT, developed by Yu,⁴⁹ uses a combination of dynamic multileaf collimation and arc therapy. The shape of the field formed by the MLC changes continuously during gantry rotation. Multiple superimposing arcs are used, and the field shape for a specific gantry angle changes from one arc to the next appropriately so that the cumulative fluence distribution of all arcs is equal to the desired distribution. Arc therapy is discussed in a recent review of various intensity-modulated techniques.⁵¹

In addition to these approaches, the University of Michigan has used the so-called multisegment approach in which each of a number of beams is divided into multiple segments.⁵² One segment for each beam frames the entire target while the others spare one or more normal structures. Each segment is uniform in intensity. The weights of segments of all beams are optimized to produce the desired treatment plan. The treatments are delivered as a sequence of multiple uniform field segments. A similar approach previously was proposed by Mohan et al.⁵³ In almost all of these significantly different treatment-delivery approaches, the underlying principles of optimization are similar, although the specifics may be quite different.

FIGURE 10.2. Commercial serial tomotherapy delivery hardware mounted on a conventional linear accelerator. A: View looking into the collimator toward the radiation source. A leaf pattern is shown that highlights the system’s capability for delivering complex fluence patterns. B: The multileaf collimator mounted to a conventional linear accelerator. C: Modern tomotherapy TomoHD^® machine. (C used with permission by Accuray, Incorporated, Madison, WI.)

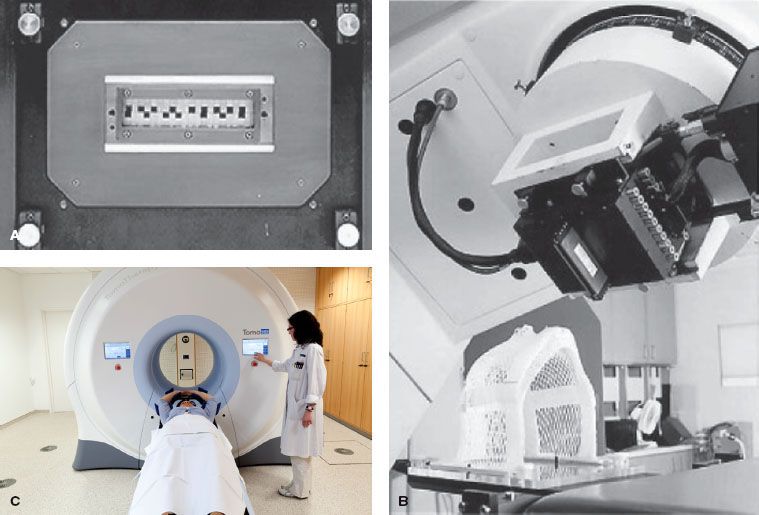
FIGURE 10.3. A: A typical multileaf collimator used for delivery of intensity-modulated radiation therapy looking toward the radiation source. In the dynamic mode, the leaves move back and forth or sweep across the field continuously to form the sequence of required field shapes while the beam is on. In the static or step-and-shoot mode, the beam is turned off when the leaves move to form the required field shapes. B: Cutaway diagram of linac head, Varian Clinac^®. (Courtesy of Varian Medical Systems, Palo Alto, CA.)

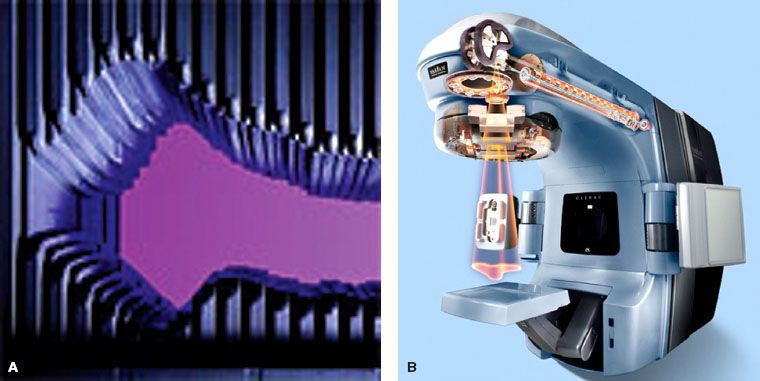
FIGURE 10.4. Overview of a typical intensity-modulated radiation therapy planning and delivery process.

FIGURE 10.5. Comparison between traditional (left) and intensity-modulated radiation therapy (IMRT) (right) optimization processes. (Reprinted from ICRU Report 83: prescribing, recording, and reporting photon-beam intensity-modulated radiation therapy [IMRT]. J ICRU 2010;10[1]:1–106, with permission.)

THE IMRT PROCESS OVERVIEW

As mentioned previously, there are significant differences in 3DCRT and IMRT concepts and processes. However, there are also many similarities. In particular, IMRT relies on many of the same imaging, dose calculations, plan evaluation, quality assurance (QA), and delivery tools as 3DCRT.

The IMRT planning, QA, and delivery phases of the dynamic or static MLC process are summarized in Figure 10.4. Figure 10.5 shows the steps in each phase of the IMRT optimization process. The tomotherapy process is similar, except that the fixed-beam angle selection is replaced by selection of the slice thickness and, for serial tomotherapy, the gantry rotation angles.

In the preparatory phase of the IMRT process, volumes of interest (such as tumors and normal organs) are delineated on 3D CT images,⁵⁴ often with assistance from other coregistered imaging modalities. The second imaging technique most often used is magnetic resonance imaging (MRI); the latter has an advantage over CT in that it can provide both structural and physiologic information.⁵⁵ Other imaging modalities such as positron emission tomography (PET) use intrinsic or externally added molecular markers to visualize specific metabolic processes or cellular phenotypes.^56–60 Also, the desired objectives in the form of an objective function, its parameter values, and the IMRT fractionation strategy are specified, and beam configuration is defined. Typically the objective function⁶¹ assigns a weighted “cost” to the square of the difference between the desired 3D fluence distribution and that calculated at a given iteration. The software attempts to minimize the costs—maximizing dosage to the tumor volume and minimizing exposure of normal tissues.

In the treatment-plan optimization phase, an iterative process is used to adjust and set the intensities of rays of each beam (or portion of the arc) so that the resulting intensity distributions yield the best approximation of the desired objectives. The IMRT plan then is evaluated to ensure that the trade-offs made by the optimization system are acceptable. If further improvement is deemed necessary and possible, the objective function parameters are modified and the optimization process is repeated until a satisfactory treatment plan is achieved.

In the leaf sequence-generation phase, the intensity distributions are converted into sequences of leaf positions. It is conceivable that certain dose distributions cannot be delivered as a result of the leakage characteristics of the delivery devices. Therefore, in most treatment-planning systems, the leaf sequences are used in a reverse process to calculate the dose distributions they are expected to deliver. These dose distributions, called the deliverable dose distributions, are evaluated for clinical adequacy. If necessary, objective function parameters are further adjusted to produce an intensity distribution that leads to a deliverable dose distribution that meets the desired objectives. This is the practice in most systems. However, in some systems, the leaf sequence-generation process is incorporated into the IMRT plan optimization loop so that the optimized and deliverable dose distributions are identical. More details on this are given later in this chapter.

The leaf sequences then are transmitted to the treatment machine and used to verify that the dose distribution that will be delivered to the patient is correct and accurate. The patient then is set up in the usual fashion and treated. In general, the entire treatment is delivered remotely without the need to re-enter the treatment room in between fields.

PREPARATORY AND IMRT PLANNING PHASES

This section discusses each of the steps of the preparatory and IMRT plan design phases. For reasons of clarity, the order in which these steps are discussed is not the same as the order in which they occur as shown in Figure 10.5. Figure 10.6 sketches the quality assurance process.

Imaging and Volumes of Interest

ICRU 83 presents updated definitions for the assorted volumes that will form the skeleton of the treatment plan.¹ Conceptually, the volumes contain three types of tissue: (a) malignant lesion, (b) otherwise normal tissue near the tumor that is already or likely to be infiltrated by microscopic disease, and (c) more distant normal tissue and organs. The quoted definitions that follow are from ICRU 83.

•   Gross tumor volume (GTV): “The GTV is the gross demonstrable extent and location of the tumor. The GTV may consist of a primary tumor (primary tumor GTV or GTV-T), metastatic regional node(s) (nodal GTV or GTV-N), or distant metastasis (metastatic GTV, or GTV-M)”.¹ They note that in some cases it may not be possible to differentiate expanding primary lesions from nearby metastatic disease. The GTV for IMRT is always defined from anatomic images, usually CT with or without MRI, and increasingly supplemented by PET.

•   Clinical target volume (CTV): “The CTV is a volume of tissue that contains a demonstrable GTV and/or subclinical malignant disease with a certain probability of occurrence considered relevant for therapy. There is no general consensus on what probability is considered relevant for therapy, but typically a probability of occult disease higher than from 5% to 10% is assumed to require treatment”.¹ The volumes outside the GTV encompassed by the CTV will depend a great deal on the particular tumor (e.g., with high or low propensity for lymph node extension). In the past, the CTV was effectively the GTV (including affected nodes) plus a 1- to 2-cm margin. The current definition stresses more the physiologic criteria based on the specifics of disease spread for each tumor. Gregroire et al. have compiled studies on CTV margins into a book.⁶² In postoperative situations, following an R0 or R1 resection, there is no gross tumor so only the CTV need be defined. Readers are strongly encouraged to consult ICRU 83 for details.

•   Planning target volume (PTV): “The PTV is a geometrical concept introduced for treatment planning and evaluation. It is the recommended tool to shape absorbed-dose distributions to ensure that the prescribed absorbed dose will actually be delivered to all parts of the CTV with a clinically acceptable probability, despite geometrical uncertainties such as organ motion and setup variations”.¹

•   Organ at risk (OAR): “The OAR or critical normal structures are tissues that if irradiated could suffer significant morbidity and thus might influence the treatment planning and/or the absorbed-dose prescription. In principle, all non-target tissues could be OARs. However, normal tissues considered as OARs typically depend on the location of the CTV and/or the prescribed absorbed dose”.¹ All normal tissue exposed to radiation during treatment is at risk, but the OAR is generally taken to be rather more specific—structures in the immediate vicinity of the PTV, sparing of which may demand specific recontouring of the CTV or PTV. Historically, OARs have been loosely grouped into “serial” or “parallel” organs or a combination of the two, following the work of Withers et al. using the concept of functional subunits in each organ.^64,65 Serial organs, such as the spinal cord, can suffer unacceptable damage if only a small portion is irradiated, whereas parallel organs, such as the liver, can suffer loss of a portion without total loss of function.

•   Planning organ at risk volume (PRV): “As is the case with the PTV, uncertainties and variations in the position of the OAR during treatment must be considered to avoid serious complications. For this reason, margins have to be added to the OARs to compensate for these uncertainties and variations, using similar principles as for the PTV. This leads, in analogy with the PTV, to the concept of PRV”.¹ As with the OAR itself, margins in the PRV will be affected by the serial or parallel attributes of the adjacent tissues.

•   Remaining volume at risk (RVR): “The RVR is operationally defined by the difference between the volume enclosed by the external contour of the patient and that of the CTVs and OARs on the slices that have been imaged”.¹ Definition of an RVR and its inclusion in the treatment plan (at least in the form of dose constraints) is essential in IMRT. Without such limits, the optimization software could craft excellent dose distributions for the CTV and OAR but cause toxic irradiation levels in otherwise uncontoured tissues.

•   Treated volume (TV): “The TV is the volume of tissue enclosed within a specific isodose envelope, with the absorbed dose specified by the radiation oncology team as appropriate to achieve tumor eradication or palliation, within the bounds of acceptable complications”.¹ The TV is what is physically deliverable given limitations of beam collimation and homogeneity and, more importantly, the risks of treatment-associated morbidity acceptable to the oncologist and the patient. ICRU 83 proposes that, in conformity with its proposal for proton therapy, the TV be defined as the dosage received by 98% of the PTV. This serves as a measure of the minimum absorbed dose, and is also referred to as D_{near minimum}. In an analogous manner, a D_{near maximum} is defined as D_2%, the dose received by 2% of the PTV receiving the highest fluence. Readers are referred to Section 3 of ICRU 83.

It should be noted that the GTV, CTV, and OAR represent volumes based on anatomic and physiologic judgments on the location of malignant growths or normal tissues in danger from metastatic spread and/or treatment-induced toxicity. These are independent of the particular irradiation protocol employed (i.e., 3DCRT, IMRT, or particle beams). The PTV, PRV, and TV are intimately tied to the specific radiation therapy used.

FIGURE 10.6. Intensity-modulated radiation therapy (IMRT) process: Quality Assurance (QA) and delivery phase.

Beam Configurations

Systems Using Fixed Intensity-Modulated Fields

The beam configuration can have a significant impact on the quality of an optimized IMRT plan. It may be argued that, because of the greater control over dose distributions afforded by optimized intensity modulation, the fine-tuning of beam angles may not be as important for IMRT as it is for standard radiotherapy. However, optimization of beam angles may find paths least obstructed by critical normal tissues, thus facilitating the achievement of desired distribution with a minimum of compromise.

Beam-angle optimization, however, is not a trivial problem. There have been some attempts to solve this problem,^66–67,68 and advances in mathematical operations research applied to the problem have been reviewed recently.⁶⁹ To appreciate the magnitude of the problem, consider the following example. If the angle range is divided into 5-degree steps, nearly 60,000 combinations would need to be tested for three beams, nearly 14 million combinations for five beams, nearly 1.5 billion combinations for seven beams, and so on. Considering the magnitude of the search space, none of the optimization methods is likely to be able to demonstrate a significant improvement in treatment plans, let alone find a truly optimum combination when the number of beams is five or more. Furthermore, the beam-angle optimization problem is known to have multiple minima,⁷⁰ which means that fast gradient-based optimization techniques may fail. Stochastic methods,^71,72 in principle, should avoid the local minimum problem but may present excessive computing time demands. These should prove less of a problem in the near future, especially with the use of dedicated parallel processors, which can drastically reduce computation time. For a review see Pratx and Xing.⁷³

Another question that may be asked is how many beams are optimal. In principle, a larger number of beams would provide a larger number of parameters to adjust and therefore a greater opportunity to achieve desired dose distributions. (Thus, in theory, a rotational beam would be the ultimate.) However, for fixed-beam IMRT, it may be desirable to minimize the number of beams to reduce the time and effort required for planning, QA, dosimetric verification, and delivery of treatments. Fewer intensity-modulated beams would be needed if beam angles were optimized than if the beams were placed at equiangular steps. Calculations by Webb⁹ indicate that seven or nine fields give adequate conformal dose distributions for both serial tomography and fixed-gantry IMRT.

Figure 10.7 compares prostate treatment plans employing different numbers of fields using 3DCRT, serial tomography, and step-and-shoot IMRT. Consistent with published experience, the plan quality improves but the incremental improvement diminishes with increasing number of beams. Optimum nonuniform placement of beams can further improve dose distribution. Figure 10.8A, B shows a head and neck IMRT case for two different beam angles. The patient, treated with the beam configuration shown in Figure 10.8A, developed significant mucositis at the early phase of treatment. This was consistent with the “horn” in dose distribution shown by the arrow. Revising the beam-angle arrangement as shown in Figure 10.8C led to improved dose distribution, shown in Figure 10.8D.

In general, it is most advantageous to place beams so that they are maximally avoiding each other and the opposing beams with the stipulation that directions that overlap significant obstructions, such as heavily attenuating bars in the treatment couch, be avoided. For simplicity, beams often are constrained to lie in the same transverse plane. However, noncoplanar beams will provide an additional degree of freedom and potentially an additional gain in the quality of treatments. It should be noted that the beam configurations used for 3DCRT may not be optimal for IMRT.⁷⁴

Although reducing the number of beams is a desirable goal for IMRT delivered with several fixed-gantry angles and dynamic MLC, it should not be the overriding consideration. IMRT can be planned and delivered automatically in times not significantly different from the times for much simpler conventional treatments. Therefore, the delivery times for six to 20 beams may be quite acceptable. Keep in mind, however, that some of the current linear accelerators are limited in their ability to accurately deliver a large number of intensity-modulated beams each with a very small number of monitor units.⁷⁵

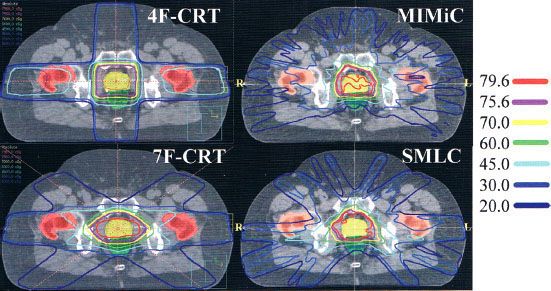
FIGURE 10.7. Typical isodose distributions for treating prostate cancer from (1) a four-field three-dimensional conformal radiation therapy (3DCRT) plan; (2) a seven-field 3DCRT plan; (3) an intensity-modulated radiation therapy (IMRT) plan delivered by serial tomotherapy using MIMiC (NOMOS Corp, Sewicky, PA); and (4) a 10-field step-and-shoot segmental multileaf collimator (SMLC) plan. (Reprinted from Chao et al. Practical essentials of IMRT, 2nd edition. Philadelphia: Lippincott Williams & Wilkins, 2005, with permission.)

Systems Using Rotating Slit (Tomotherapy) Approach

Tomotherapy delivery has substantial differences from fixed-portal IMRT. Mackie has published a historical review of tomotherapy, intertwined as it is with his career.⁷⁶ The linear accelerator rotates during delivery, and the beam is modulated during rotation. Typically, the modulation is subdivided into small gantry angle ranges (e.g., 5 degrees) and the beam is independently modulated at each gantry angle. Each leaf is used to deliver a single rotating pencil. The pencil-beam modulation is conducted for each leaf by opening that leaf for a fraction of the gantry range consistent with the fractional fluence to be delivered from that gantry angle. For example, for a 5-degree-angle-range bin, if a leaf is to deliver 50% fluence, the leaf will be open for 2.5 degrees over the 5-degree range. Because of geometric constraints of modulating the radiation fan beams, only one or two thin planes can be treated with each rotation. The Peacock system,²⁶ for instance, uses two banks of opposing leaves projecting to 1.7 or 3.4 cm, depending on user-selected mechanical stops. This delivers modulated beams to two abutting, independently modulated planes. The helical tomotherapy unit uses a single leaf bank with a backup collimator that allows the radiation field width to be continuously adjusted. Narrower leaf widths provide higher spatial resolution for modulation but require more treatment arcs and consequently more delivery time. The current TomoHD MLC uses tungsten leaves 10 cm thick (in beam direction) and with a width of 0.625 cm. Leaves are driven pneumatically and switch in 20 msec.

Aperture Margins

IMRT has the inherent capacity to reduce margins attributable to the beam penumbra. When a photon beam traverses the body, it is scattered, depositing dose not only along the path of each ray of the beam but also at points away from it. The electrons knocked out by the incident photons travel laterally to points in the neighborhood of each ray, depositing dose along the way. Near the middle of a uniform beam, outgoing electrons are offset by incoming electrons and equilibrium exists. However, at and just inside the boundaries of the beam, there are no incoming electrons to balance electrons flowing out of the beam. Therefore, a “lateral electronic disequilibrium” exists that leads to a dose deficit inside the boundaries of beams. For lower-energy beams and at large depths, scattered photons significantly contribute to this effect also. The conventional approach to overcome this deficiency is to add a margin for the “beam penumbra” to the PTV so that the tumor dose is maintained at the required level.

For IMRT plans, there is another method to counterbalance the dose deficit. The intensity of rays just inside the beam boundary may be increased. Because some of the increased energy must also flow out, a very large increase would be required if the margin for the penumbra were set to zero or to a very small value. Therefore, an increase in boundary fluence alone is not enough. A combination of an increased fluence and the addition of a margin, albeit a much smaller one, is a better solution. This reduction in margin can be exploited quite usefully to reduce the volume of normal tissues exposed to high doses of radiation with a corresponding reduction in toxicity and a further potential for dose escalation.

The beam–boundary-sharpening and margin-reduction feature of IMRT can be taken advantage of only if the dose-computation method is able to adequately take into account the lateral transport of radiation⁷⁷ and if the intensity matrix grid size is sufficiently small. Initially, dose distribution for a given configuration of beams is computed by taking lateral transport into consideration. In each optimization iteration, the intensity distribution first is designed ignoring lateral transport. At the end of the iteration, the dose distribution is recalculated, thereby incorporating the effects of field-shaping devices on lateral transport and revealing the resulting deviations from the anticipated dose distribution. In the next iteration, ray intensities are adjusted further to rectify the deviations, and so on.^50,78 Carrasco et al. compared several dose-computation algorithms in lung phantoms.⁷⁷

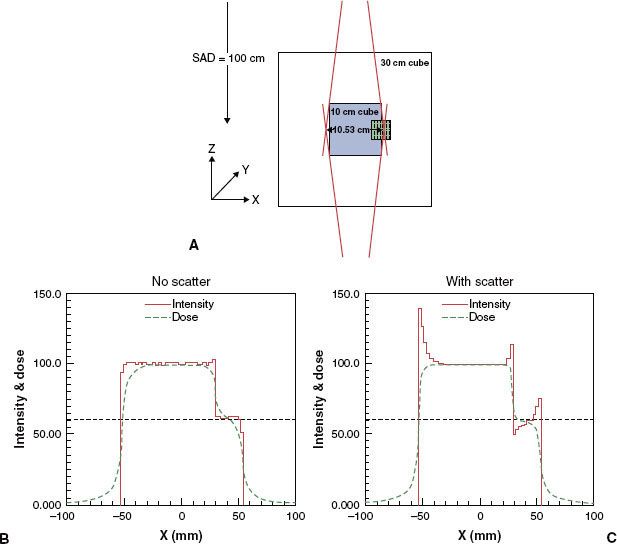
A schematic example shown in Figure 10.9 illustrates the issues involved. Figure 10.9A shows a normal organ overlapping the target volume. The target volume is being irradiated by two parallel-opposed beams. It is desired that the dose to the region of overlap be 60% of the target dose. If more dose is delivered, damage to the normal organ may result; but lower than the desired dose may cause local failure. If the role of lateral transport in optimization is ignored, the intensity resulting from the optimization process is essentially a step function, as shown in Figure 10.9B (solid curve). The corresponding dose distribution (the dotted curve) shows a dose deficit inside the high-dose target volume as well as the outside edge of the region of overlap and an excess of dose in the region of overlap adjacent to the high-dose volume. If lateral transport is incorporated by adjusting fluence, the fluence and dose patterns shown in Figure 10.9C result. Fluence is increased at both boundaries. It also is increased in the high-dose side of the interface with the overlap region and decreased on the lower-dose side. The dose is now much closer to the desired dose. Comparing Figures 10.9B and 10.9C, it also appears that a modest increase in fluence just inside the boundary does not lead to a perceptible increase in dose outside the beam boundary. This is presumably the result of the fact that the excess dose flowing out of the target periphery is deposited in a much larger volume of tissue. A reduction of margins attributable to penumbra by as much as 8 mm has been found to be feasible for prostate treatments.^50,78

FIGURE 10.8. A patient with carcinoma of the base of the tongue was treated with intensity-modulated radiation therapy. A and B depict the beam angle arrangement and the resulting isodose distribution. Arrow on (C) indicated a “horn” of high dose to the left oral tongue and buccal mucosa. Rearrangement of anterior beam placement as shown in (B) led to improvement of dose distribution to the normal mucosa of the left anterior oral cavity (D).

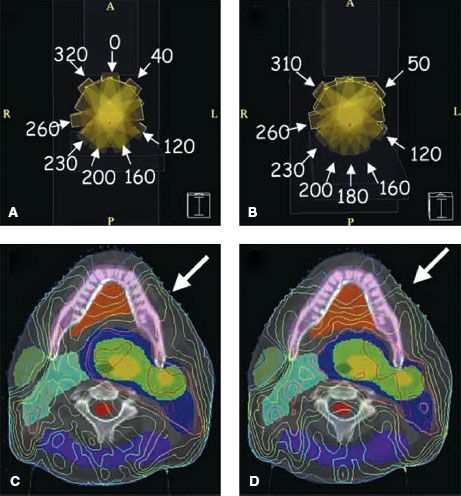
FIGURE 10.9. A schematic example illustrating the sharpening of penumbra with intensity-modulated radiation therapy.

IMRT Fractionation

In principle, conventional fractionation strategies can be used to design IMRT plans as well. For example, in a strategy similar to the conventional 1.8-Gy to 2-Gy/fx schedule, a major portion of the dose could be delivered in the initial phase using uniform fields designed with standard 3D conformal methods followed by an IMRT boost. Alternatively, separate IMRT plans could be designed for both the initial large-field treatment and the boost treatment. It may be intuitively obvious that, if a large portion of the dose already has been delivered using large fields, it may be very difficult, if not impossible, to achieve a high level of dose conformation with the remaining fractions in the IMRT-boost phase.¹⁵ As indicated earlier in this chapter, IMRT may be most conformal if all target volumes (gross disease, subclinical extensions, and electively treated nodes) are treated simultaneously using different fraction sizes.¹⁵ Such a treatment strategy has been called the simultaneous integrated boost (SIB).^11,12,15,19 Mackie et al. had also indicated the possibilities for irradiation boost in their first paper on serial tomography.⁷⁹ The SIB IMRT strategy not only produces superior dose distributions but also is an easier, more efficient, and perhaps less error-prone way of planning and delivering IMRT because it involves the use of the same plan for the entire course of treatment. Furthermore, in many cases, there is no need for electron fields, and the nodal volumes can be included in the IMRT fields; thus, the perennial problem of field matching⁸⁰ encountered in the treatment of many sites is thereby avoided.

Because each of the target regions receives different doses per fraction in the SIB IMRT strategy, prescribed nominal (physical) dose and dose per fraction must be adjusted appropriately. The adjusted nominal dose and fraction size for each target region depend on the number of IMRT fractions. The fraction sizes may be estimated using an isoeffect relationship based on the linear-quadratic model and the values of its parameters (such as α/β ratios, tumor doubling time).

The effect of the modified fractionation on acute and late toxicity of normal tissues both outside and within the volumes to be treated also should be considered. Because of the improved conformality of IMRT plans, dose to normal tissues outside the target volume is typically lower than for conventional treatment plans. In addition, if the number of fractions is greater than the number of fractions used to deliver large fields in conventional therapy, the dose per fraction to normal tissues is lower. Therefore, the biologically effective dose would be lower still. However, normal tissues embedded within or adjacent to the target volumes would receive high doses per fraction and may be at higher risk. Isoeffect formulae for normal tissues also may be derived to estimate the effect of a particular fractionation strategy (see ICRU 83, pp. 36–38). These formalisms would need to incorporate regeneration and change in sensitivity over the treatment course.

The values of parameters for the computation of altered fractionation may, in theory, be obtained from published studies. Studies by Maciejewski et al.⁸¹ and Withers et al.^82–84 for example, have yielded important information for estimating tumor parameters for head and neck carcinoma. In general, the data available are limited. Furthermore, there is considerable uncertainty in the data, and there are concerns about the validity of numerous assumptions in the linear-quadratic model and the isoeffect formalism, especially with regard to normal tissues. (For an early review of the linear-quadratic model see Fowler⁸⁵). Much of the accumulated data on normal tissue complications comes from clinical experience in the era of wide-field radiation therapy, so the dosage limits reported from such studies may not be immediately applicable to IMRT. Nevertheless, various investigators have carried out the necessary calculations and adopted SIB IMRT fractionation strategies. Continued investigations and clinical trials are needed to develop more reliable time-dose fractionation models, to produce better estimates of their parameters, and to evaluate alternate SIB IMRT fractionation strategies for all sites.¹³ The following are some examples of IMRT fractionation strategies that have been used for IMRT of head and neck cancers.

In the Radiation Therapy Oncology Group H-0022 protocol for early-stage oropharyngeal cancer, 30 daily fractions (5 per week × 6 weeks) are used to simultaneously deliver 66 Gy (2.2. Gy per fraction) to the PTV, 60 Gy (2 Gy per fraction) to the high-risk subclinical disease (“levels II–IV bilaterally, Ib ipsilaterally, and level V and retropharyngeal nodes if the jugular nodes were involved”), and 54 Gy (1.8 Gy per fraction) to subclinical disease. These are biologically equivalent to 70, 60, and 50 Gy, respectively, if given in 2 Gy per fraction. For normal structures, brainstem, spinal cord, and mandible are maintained below 54, 45, and 70 Gy, respectively. The mean dose to the parotid glands is maintained below 26 Gy and/or 50% of one of the parotids is maintained below 30 Gy and/or at least 20 mL of the combined volume of both parotids is constrained to receive no more than 20 Gy. Sixty-nine patients were accrued at 14 institutions. Treatment-associated xerostomia improved following therapy, in contrast to regular radiation therapy. High locoregional control was achieved with stringent adherence to protocol guidelines.⁸⁶

The SIB strategy at Virginia Commonwealth University involves a dose-escalation protocol in which primary nominal dose levels of 68.1, 70.8, and 73.8 Gy, given in 30 fractions (biologically equivalent to 74, 79, and 85 Gy, respectively, if given in 2 Gy per fraction), are used.⁸⁷ Simultaneously, the subclinical disease and electively treated nodes were prescribed 60 and 54 Gy, respectively (biologically equivalent to 60 and 50 Gy, respectively, if given in 2 Gy fractions). Spinal cord and brainstem are maintained below 45 and 55 Gy, respectively, and an attempt is made to allow no more than 50% of at least one parotid to receive higher than 26 Gy.

At the Mallinckrodt Institute of Radiology, the SIB strategy for definitive IMRT prescribes 70 Gy in 35 fractions in 2 Gy per fraction to the volume of gross disease with margins. The adjacent soft tissue and nodal volumes at high risk were treated to 63 Gy in 1.8 Gy per fraction and simultaneously 56 Gy in 1.6 Gy per fraction to the elective nodal regions. This regimen has been shown to be well tolerated when combined with concurrent chemotherapy.⁷⁸

The most conservative normal tissue constraints for head and neck sites based on the most recent RTOG protocols (1016, 1008, 0920, and 0912) are: optic nerve and chiasm <30 Gy; eyes <30 Gy; brainstem <48–52 Gy to any 0.03 cc volume; brain <60 Gy to any 0.03 cc volume; spinal cord <45–48 Gy to any 0.03 cc volume; ipsilateral cochlea <50 Gy; parotid glands <26 Gy and at least 20 cc volume <20 Gy; submandibular glands mean <39 Gy; mandible <60 Gy; cervical esophagus mean <35 Gy; pharynx mean <40–45 Gy (for details, see www.rtog.org). Other workers^88–90 have determined dose levels to the pharyngeal constrictors above which severe dysphagia will occur: V65 Gy >30%, V55 Gy >80%, and a mean dose >60 Gy were predictive of feeding tube dependence.

Optimization of Intensity Maps

The optimization of ray intensities may be carried out using one of several mathematical formalisms and algorithms, also termed optimization engines.⁶⁹ Each method has its strengths and weaknesses. The choice depends in part on the nature of the objective function and in part on individual preference. Although the details are complex, the basic principles are not difficult to comprehend. Each ray of each beam is traced from the source of radiation through the patient. Only the rays that pass through the target volume need to be traced (plus through a small margin assigned to ensure that the lateral loss of scattered radiation does not compromise the treatment). Others are set to a weight of zero.

The patient’s 3D image is divided into voxels. The dose at every voxel in the patient is calculated for an initial set of ray weights. The resulting dose distribution is used to compute the “score” of the treatment plan (i.e., the value of the objective function that mathematically states the clinical objectives of the intended treatment).

The ray-tracing process identifies the tumor and normal tissue voxels that lie along the path of the ray. The effect of a small change in a ray weight on the score then is calculated. If the increase in ray weight would result in favorable consequences for the patient, the weight is increased, and vice versa. Mathematically speaking, the ray weight is changed by an amount proportional to the gradient of the score with respect to the ray weight. Realizing that the improvement in the plan at each point comes from rays from many beams and that each ray affects many points, only a small change in ray weight may be permitted at a time. This process is repeated for each ray. At the end of each complete cycle (an iteration), a small improvement in the treatment plan results. The new pattern of ray intensities then is used to calculate a new dose distribution and the new score of the plan, which then is used as the basis of further improvement in the next iteration. The iterative process continues until no further improvement takes place, the optimization process is assumed to have converged, and the optimum plan is assumed to have been achieved.

Many current optimization systems use variations of gradient techniques to optimize IMRT plans. These calculations are prodigious given the thousands of free parameters in variation—it was only with the advent of powerful and affordable computers that such calculations could become clinically realistic. Direct aperture optimization has been proposed as an alternative that reduces the parameter space and eliminates nonphysical dose distributions at the start; for a review see Broderick.⁹¹ The use of gradient techniques assumes that there is a single extremum (a minimum or a maximum, depending on the form of the objective function). This is indeed the case for objective functions based on variance of dose and when only ray weights are optimized. For other cases, it would be necessary to determine whether multiple extrema exist and whether such multiple extrema have an impact on the quality of the solution found. Multiple extrema have been found to exist when beam directions are optimized or when dose–response-based objective functions are used to optimize weights of uniform beams.^53,92,93 One can expect that multiple minima also exist when dose–response-based objective functions are used to optimize IMRT plans. Using simple schematic examples, it also has been shown that multiple minima exist when dose–volume-based objectives are used.⁹⁴ Although this may be the case in theory, the existence of multiple minima has not been found to be a serious impediment in dose–volume-based or dose–response-based optimization using gradient techniques. In fact, in a study of dose–volume-based IMRT optimization, Wu and Mohan⁹⁵ found that, starting from vastly different initial intensities, the solutions converged to nearly the same plans. The reasons for this have been speculated but not conclusively proven and need to be investigated further.

If multiple minima are discovered to be a factor, then some form of stochastic optimization technique may need to be considered. At the simplest, one may use a random search technique in conjunction with one of the gradient techniques. A more sophisticated stochastic technique is “simulated annealing” or its variation, the “fast simulated annealing”.^8,46,53,92 These techniques allow the optimization process to escape from the local minima traps. Other forms of stochastic approaches, such as “genetic algorithms,” also have been proposed.⁹⁶ In principle, the simulated annealing technique and other stochastic approaches can find the global minimum, but, practically, there is no guarantee that the absolute optimum has been found, only that the best among the solutions examined has been found. (This, of course, is true for gradient techniques as well.) Stochastic techniques tend to be extremely slow and should be used in routine work only if it is established that they are necessary. Nevertheless, some commercial systems have implemented the simulated annealing approach for IMRT optimization.³ Also, as noted earlier, rapid advances in parallel processing using off-the-shelf components can dramatically reduce computation times.⁷³ In 2005, Xu and Mueller reported an order of magnitude decrease in the time to process a CT image on a PC when equipped with a dedicated graphics board.⁹⁷

OBJECTIVE FUNCTIONS

Dose-Based Objective Functions

A simple example of an objective function is the criteria stated in terms of the sum of the squares of the differences of desired dose and computed dose at each point within each of the volumes of interest. That is,

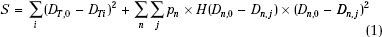
This type of objective function is called the quadratic or variance objective function. The optimization process attempts to minimize the treatment plan score S. D_T,0 in expression Eq. (1) is the desired dose to the target volume and D_n,0 is the tolerance dose of the nth normal structure. D_T,i is the computed dose at the ith voxel of the target and D_n,j is the computed dose at the jth voxel of the nth normal structure. For normal organs, the function H(D_n,j –D_n,₀) is a Heaviside step function defined as follows:

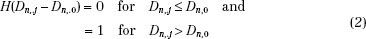
In other words, so long as the dose in a normal tissue voxel does not exceed the tolerance limit, the voxel does not contribute to the score function. The quantity p_n is the “relative penalty” for exceeding the tolerance dose.

Dose–Volume-Based Objective Functions

Purely dose-based criteria, such as the one previously described, are not sufficient. In general, the response of the tumor and normal tissues is a function of not only radiation dose but also (to varying degrees depending on the tissue type) the volume subjected to each level of dose. Currently, dose–volume-based objective functions are the most widely used clinically. Dose–volume-based objective functions are expressed in terms of the limits on the volumes of each structure that may be allowed to receive a certain dose or higher. ICRU 83 sets its IMRT reporting guidelines in terms of dose–volume criteria, and dose–volume histograms (DVHs) are a mandatory part of treatment planning.

A practical scheme to incorporate dose–volume-based objectives has been suggested by Bortfeld et al.⁹⁸ It is explained in Figure 10.10 using a simple schematic example of one organ at risk. The dose–volume constraint is specified as V(>D₁) < V₁. In other words, the volume receiving dose greater than D₁ should be less than V₁. To implement such a constraint into the objective function, we seek another dose value D₂ so that in the current dose–volume histogram V(D₂) = V₁. The objective function component for this OAR then may be written as:

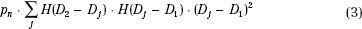
That is, only the points with dose values between D₁ and D₂ contribute to the score. Therefore, they are the only ones penalized.

For the target volumes, two types of dose–volume criteria may be specified to limit both the hot and cold spots. For instance, for the desired target dose of 80 Gy, we may specify V (>85 Gy) ≤ 5% and V (>79 Gy) ≥ 95%. In other words, the volume of the target receiving dose >85 Gy should be no more than 5%, and the volume of target receiving 79 Gy or higher should be at least 95%. Dose-based criteria can be considered as a subset of the dose–volume criteria in which the volume is set to an extreme value (0% or 100%, as appropriate). Dose–volume criteria provide more flexibility for the optimization process and greater control over dose distributions. The reason is that dose-based optimization penalizes all the points above the dose limit, whereas the dose–volume-based optimization penalizes only the subset of points within the lower end of range of dose values above the dose limit. For the example of Figure 10.10A, the dose–volume-based optimization process attempts to bring only the points between D₁ and D₂ into compliance with the constraint. In contrast, the dose-based optimization process attempts to constrain all of the points above D₁. Furthermore, dose–volume criteria are highly “degenerate” functions of dose distributions (i.e., there is a very large number of dose distributions that correspond to the same dose–volume constraint). Therefore, the optimization system has a large solution space to choose from, making it easier to find a better solution.

FIGURE 10.10. A: Incorporation of dose–volume constraints in intensity-modulated radiation therapy optimization. (Adapted from Wu Q, Mohan R. Multiple local minima in IMRT optimization based on dose-volume criteria. Med Phys 2002;29[7]:1514–1527.) B, C: Limitations of dose–volume-based criteria (see text).

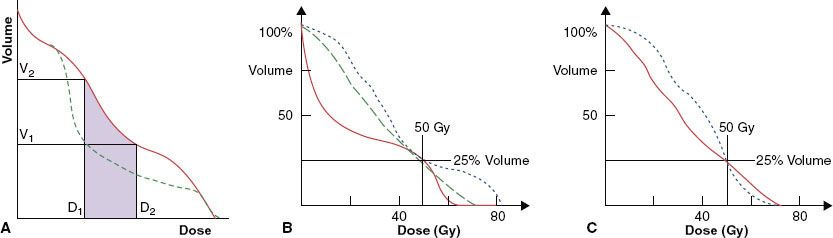
Limitations of Dose–Volume-Based Objective Functions

Dose–volume-based criteria have been demonstrated to have limitations. To illustrate one such limitation, consider the example in Figure 10.10B of a normal structure for which a constraint has been specified that no more than 25% of the volume is to receive 50 Gy or higher. All three DVHs shown meet this criteria. However, the DVH represented by the solid curve clearly causes the least damage. One can argue that we can overcome this limitation by specifying multiple dose–volume constraints or even the entire DVH. However, as illustrated in Figure 10.10C, this would be too limiting. Multiple DVHs could lead to an equivalent injury to a particular organ, but each DVH may produce a different effect on other organs and the tumor. When this happens, DVHs usually cross each other, as shown in Figure 10.10C. Only one of them is optimum so far as the tumor and other organs are concerned.

To overcome the limitations of dose–volume-based criteria, they may be supplemented with biologic (or dose–response-based) criteria, for instance, in terms of such indices as tumor control probability (TCP), normal tissue complication probabilities (NTCPs), and equivalent uniform dose (EUD).⁷⁷ Dose–response-based objective functions are the subject of ongoing investigations.^53,99 The ICRU currently includes NTCP and EUD projections in its Level 3 reporting (i.e., still investigative). The report (see p. 51) notes that most of the tissue tolerance data go back to the period before 3D imaging, but they do cite newer prospective studies involving 3DCRT or IMRT.^100,101

FIGURE 10.11. Effect of adjusting dose-prescription parameters on the resulting treatment plan. The parotid gland and target are shown in green and blue, respectively. Plan C emphasizes parotid sparing, and plan F emphasizes tumor coverage. (Interested readers should view the full set of six plans as presented in the original paper. From Chao KS, Low DA, Perez CA, et al. Intensity-modulated radiation therapy in head and neck cancers: the Mallinckrodt experience. Int J Cancer 2000;90[2]:92–103.)