Envisioning the Application of Systems Biology in Cancer Immunology

Fig. 23.1

Sketch of an advanced systems biology workflow

Step 1. In clinical cohorts of, for example, cancer patients vs. healthy individuals, high-throughput data of tissue and/or plasma concentrations for proteins, RNAs, or other molecules are collected together with biometric data from the patients. The data are processed, integrated, and analyzed using statistical models aiming to group them according to their gene expression vs. the progression status profiles. In this way, one can obtain cancer-associated genetic signatures relevant to the phenotype under investigation (e.g., chemoresistance, aggressiveness, metastatic potential). These signatures account for a group of genes, proteins, miRNAs, or other molecules, for which a robust statistical correlation is found between their combined expression pattern and the investigated cancer phenotype [5].
Step 2. Relevant biomedical and clinical knowledge is gathered from databases, computational algorithms, and publications inspected via manual curation or text mining. This information is used to find feasible biochemical interactions (i.e., protein-protein interactions, transcriptional regulation, etc.) between compounds of the genetic signature, but also with other kinases, transcription factors, or microRNAs, all of them relevant to the investigated cancer phenotype. In this way, we can construct a network of cross-talked intracellular pathways relevant to the investigation of the aimed cancer phenotypes. Furthermore, similar networks can be constructed for the cell types in the tumor microenvironment related to the phenotype investigated. Since tumor cells and cells in the microenvironment secrete cytokines and other molecules signaling each other, the obtained network is one of cell-to-cell communication, accounting for the tumor-microenvironment interaction in the cancer phenotype under investigation. The network obtained is often called regulatory map, nothing but a visualization of the state of the art of the biochemical and biomedical knowledge about the cancer phenotype under investigation. Tools from network biology can be used to dissect the topology of the regulatory map and isolate regulatory motifs relevant for the derivation of hypothesis and experiments [22, 8].
Step 3. The parts of the network relevant to the biomedical scenarios which are related to the investigated cancer phenotype are translated into a mathematical model. The model consists of mathematical equations, in an adequate modeling formalism, accounting for the time evolution of the expression and/or activation status of the network compounds, as well as their connection to the phenotypes. Many modeling formalisms are available, all of which are with advantages and disadvantages [6]. To circumvent some of these disadvantages, one can combine them in hybrid models. For example, we have combined interconnected sub-modules in ordinary differential equations and Boolean logic [23]. Ordinary differential equations are excellent tools to analyze the nonlinear behavior of signaling pathways with multiple, nested feedback and feedforward loops, while logic models are an ideal representation of massive transcriptional networks. The combination of both model types allows the analysis of large-scale, nonlinear transcriptional and posttranscriptional networks and their connection to cancer cell phenotypes [23].
Step 4. Additional quantitative in vitro/in vivo experimental data are used to improve the biological characterization of the model, that is, to make it more accurate in terms of prediction of the relevant biomedical scenarios. This is often called model calibration and allows assigning appropriate values to model parameters and other model features. Alternatively, this process also allows for the validation of hypothesis concerning the structure and regulation of the network in the biomedical context analyzed; in this case, iterative cycles of modeling and experimentation can be used to formulate, refine, prove, or disprove hypothesis concerning the existence and relevance of given biochemical interactions [24]. With the use of the mathematical model, one can analyze spatiotemporal regulatory features of the network that elude the elucidation via conventional experimentation, like self-sustained oscillations, or bistability.
Step 5. In recent years, various studies have proved that a well-calibrated, data-driven mathematical model can be used with predictive purposes in the context of molecular oncology. The underlying idea is to use model simulations and other tools to assess existing therapies in a personalized manner, design new therapies, or detect sets of biomarkers for cancer prognosis. In a final step, one has to go back to the bench and design additional in vivo/in vitro experiments to confirm the model predictions. Alternatively, the model predictions can be combined with virtual screening and other techniques from computational biology and immunoinformatics and used in the process of drug discovery or vaccine development. For example, potential drug targets, identified via mathematical modeling, can be used as most promising candidates in a drug screening procedure via protein docking-based techniques [21].

23.3 Does Cancer Immunology Need a Systems Biology Approach?

In our opinion, the immune system is one of the most complex realizations of a biological system. The immune system is actually a multi-scale system (Fig. 23.2). It involves many types of cells, whose fate, proliferation, or activation status is controlled by feedback loop-regulated pathways. These pathways very often cross talk creating complex networks. Furthermore, the activation status of given immune cells depends on other immune cells by direct contact or through secretion of local or global signaling molecules, especially cytokines. In this way, the immune system is enriched in cell-to-cell communication circuits and autocrine loops. When we further consider the interaction between the immune system and a tumor, the picture becomes more systemic-like. Tumor cells and the immune cells in the surroundings communicate through chemical signals and affect each other’s fate. Tumors secrete antigens (Ags) detected by immune cells like dendritic cells, while cells from the immune system secrete cytokines and antibodies (Abs) targeting the tumor cells. In addition, features of the microenvironment in which the tumor is hosted can affect the response of the immune cells. Finally, all these processes are happening at the same time and affecting each other at different biological and temporal scales. Altogether, this suggests the use of a systemic strategy to tackle the complexities of the tumor-immune system interaction. In the following section, we discuss some published results that illustrate how systems biology can be used in the context of oncology and tumor immunology.

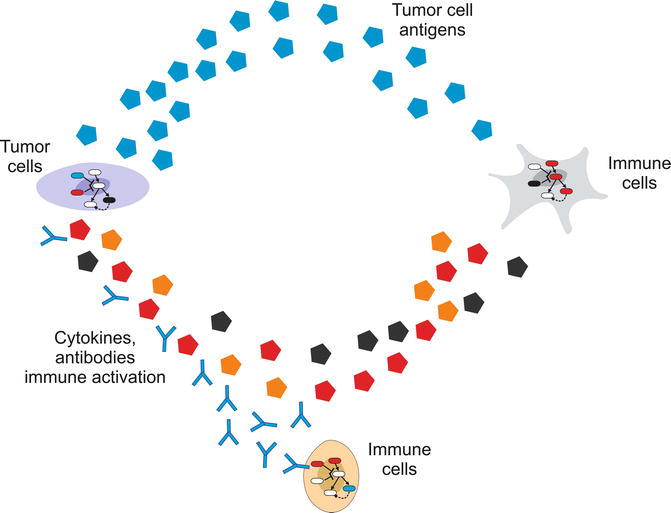
Fig. 23.2

Tumor-immune cells interaction envisioned as a multilevel system. The immune system involves many types of cells, whose fate is controlled by feedback loop-regulated pathways, but also some immune cell types affect the activation of others by direct contact or local/global signaling molecules. Furthermore, the immune system and the tumor are affected by cell-to-cell communication circuits involving tumor antigens and immune cell-secreted antibodies and cytokines

23.4 A Quick View on Current Results

23.4.1 Computational Biology, Bioinformatics, and High-Throughput Data Analysis Used in the Design of Immune Therapies for Cancer

The availability of next-generation sequencing along with omics data shifted the paradigm for cancer treatment and opens the doors toward possible cancer immunotherapy. Like traditional vaccines that stimulate the host immune system to recognize and destroy pathogens, cancer vaccines are aimed to generate an immune response that differentiates tumor cells from the normal cells for their possible elimination. For several of the pathogenic cancers, such as cervical cancer caused by human papillomavirus; hepatocellular carcinoma caused by hepatitis B and hepatitis C virus; Hodgkin lymphoma by Epstein-Barr virus; T-cell leukemia by human T-cell leukemia virus; and Kaposi’s sarcoma by Kaposi’s sarcoma herpes virus, there has been considerable success in designing cancer vaccines in the past, and many of them are currently in use or in the advanced stages of clinical trials. Most of these vaccines are designed in a similar way as the traditional epitope-based vaccine-designing approaches. However, for the non-pathogenic cancer, the major challenge for the immune system is to distinguish cancer cells from the healthy cells in order to activate B lymphocytes to produce Abs or T lymphocytes. In order to trigger antibody-dependent cellular cytotoxicity or phagocytosis to kill cancer cells, these Abs need to recognize specific proteins normally on the outer membrane of the cancer cells [25]. T lymphocytes have the capacity to selectively recognize peptides (antigens) derived from self/ nonself proteins attached with major histocompatibility complexes on the antigen-presenting cells (APCs). The use of cytotoxic T cells (CTLs), dendritic cells (DCs), and monoclonal antibodies is now a well-established strategy to design potential cancer immunotherapeutics [26].

The major challenge in the development of cancer vaccines is that Ags normally recognized by the immune system are expressed as the “self”-Ags to which the immune system is already tolerized. Therefore, the potential approach is to identify non-tolerogenic, tumor-associated antigens (TAAs) suitable to develop Ag-specific anticancer vaccines [27]. In spite of success in other infectious diseases, the use of small self-peptides as Ags in cancer vaccines did not attain much interest in the past because of their poor immune response and minimal therapeutic benefits. Most of these free peptides are likely to have a short half-life and poor pharmacokinetics properties and are thus rapidly cleared before they can be loaded on the dendritic cell surfaces in the complex with MHC molecules to stimulate CD8⁺ and CD4⁺ T cells for the initiation of adaptive immune responses [28]. However, the coadministration of suitable dendritic cell-activating adjuvant along with short TAA peptides was shown to boost immune responses in advanced melanoma [29] and vulvar intraepithelial neoplasia patients [30]. These studies generated the hope to design effective therapeutic cancer vaccines.

In order to avoid the “self”-recognition that normally results in the weakened immune responses for cancer vaccines, researchers have validated the use of DNA vaccines in preclinical studies where the tumor-derived sequences were initially fused with the genes encoding microbial proteins [31]. This strategy helped T helper cells in the induction of Abs against tumor Ags along with epitope-specific antimicrobial CD8⁺ T cells. Another example PROSTVAC, a DNA vaccine for prostate cancer, which includes recombinant vaccinia virus encoding prostate TAAs along with adhesion molecules and DCs stimulators, is already in the clinical trial phase III [32]. Besides, several monoclonal antibodies (mAbs) and other small molecules such as kinase inhibitors, angiogenesis inhibitors, proteasome inhibitors, and molecular receptor blockers are also combined with immunotherapy for developing targeted anticancer therapies [33]. Many Abs boost the immune response against cancer cells. Ofatumumab and ipilimumab are two such mAbs recently approved by the US FDA. While ofatumumab targets CD20 protein which inhibits early-stage B-lymphocyte activation in chronic lymphocytic leukemia [34], ipilimumab specifically targets cytotoxic T-lymphocyte-associated antigen 4 (CTLA 4) that provides inhibitory signal for activated T cells [35]. Unconventionally, mAbs are also shown to target intracellular oncoproteins; this finding opens a new possibility to predict potential targets for TAA discovery [36, 37].

Still, the detection of effective non-tolerogenic TAAs from extra-/ intracellular oncoproteins is one of the major challenges in cancer immunotherapy. To recognize TAAs, one has to carefully investigate sites for cancer-specific point mutations, chromosomal aberrations, splicing variants, alternative reading frames along with overexpressed genes, and other regulatory elements (transcription factors, miRNAs, etc.) [38–40]. For many of these data mining approaches, well-established computational pipelines already exist in the public domain. For therapeutic cancer vaccines, the idea is to either amplify or induce new immunogenic responses in cancer patients based on CD8⁺ or CD4⁺ T-cell responses by recognizing differentially expressing TAAs from microarray data repositories [41]. One of such database is Oncomine, which has a huge repository of gene expression profiles from microarray studies to identify differentially expressing genes in various stages of major types of cancer [42]. These data analysis pipelines facilitate the discovery of novel cancer biomarkers and drug/vaccine candidates. In the following section, we will describe the use of bioinformatics tools and computational pipelines to discover potential cancer vaccine candidates with a case study.

23.4.1.1 Case Study: Computational Approaches to Design DNA Vaccine for Cervical Cancer Caused by Human Papillomavirus

Cervical cancer is the most common and slow-growing malignant cancer present in the tissues of the cervix or cervical area in women. Persistent infection with human papillomavirus (HPV) is considered to be one of the major etiological factors for cervical cancer [43]. More than 100 different types of human papillomaviruses (HPV) have been identified [44] and categorized into high-risk and low-risk strains. A total of 16 different high-risk strains have already been identified, among them strain 16 and 18 are together responsible for approximately 70 % of all cervical cancer cases [45]. Two HPV vaccines GARDASIL and CERVARIX are currently in use as prophylactic vaccines and offer no therapeutic benefit for patients already infected with the virus or those with precancerous lesions or cervical cancer [46]; also they are not completely effective against all high-risk strains of this virus. In contrast, therapeutic vaccines generate a T-cell immune response to eliminate existing viral infection. Epitope-based vaccines provide a specific strategy for prophylactic and therapeutic application of pathogen-specific immunity. The identification of epitopes suitable for diagnostic use and for therapeutic or prophylactic intervention is clearly a crucial prerequisite of these strategies. The selection of immunogenic, consensus, and conserved epitopes from proteins of major high-risk strains may provide an experimental basis for the design of very specific T-cell and DNA vaccines effective against all high-risk strains. Herein, we will highlight the computational pipeline adopted in one of our previously published research works which was used to design in silico DNA vaccines against (HPV) by using consensus epitopic sequences of L2 capsid protein from all high-risk HPV strains [47]. In addition, various computational parameters were optimized to increase the immunogenicity of the vaccine by considering multiepitopic sequences, codon optimization, CpG motifs optimization, and inclusion of promoter and other immune-stimulatory molecules. A generalized computational pipeline for the design of DNA vaccine is highlighted in Fig. 23.3. The work initiates with the detection of differentially expressing genes in cancer (non-pathogenic) or the identification of conserved immunogenic regions from pathogens involved as the major etiological agents. From the conserved regions, MHC class I and class II epitopes are predicted followed by the inclusion of proteosomal/lysosomal cleavage sites. Various computational approaches may follow to filter the immunogenic peptide such as 3D structure modeling to calculate the solvent accessibility of cleavage sites, post cleavage conservancy of epitopes, and then long half-life for proper immunogenicity using molecular dynamics simulations. The selected peptide can then be back-translated and optimized for codons and CpG motifs. In silico cloning experiments may also be performed for the selection of good expression systems to be used for vaccine development.

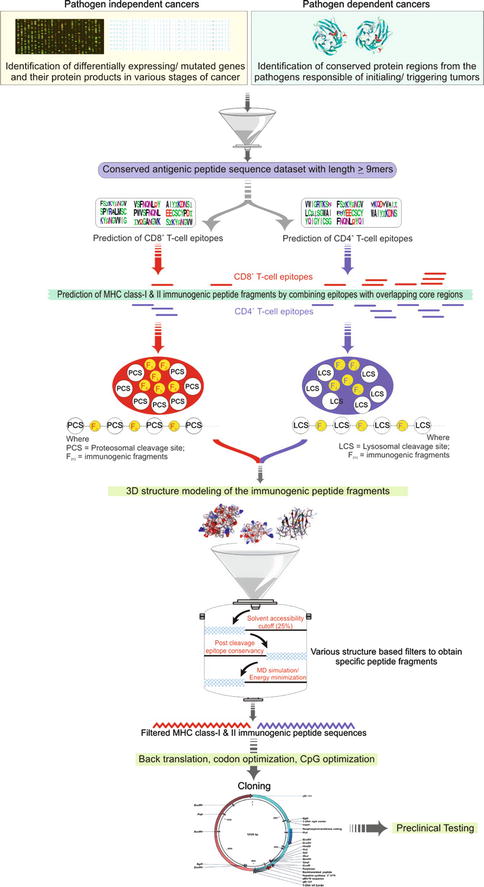
Fig. 23.3

Generalized workflow for computer-aided epitope-based DNA vaccine design

Retrieval of Sequence Data and Identification of Conserved Regions in the Protein

In case of previously designed HPV vaccines, researchers thoroughly investigated L1 and L2 capsid proteins form the virus to detect potential vaccine candidates. Some of the previous in vitro neutralization studies demonstrated high cross-reactivity with L2 antisera. We retrieved HPV L2 capsid protein sequences for various strains from the NCBI (http://www.ncbi.nlm.nih.gov) and the UniProt (http://www.uniprot.org) database. To identify conserved regions in the protein, we performed multiple sequence alignment using the ClustalX software. Based on the multiple alignment files, we identified conserved regions in the L2 capsid proteins using the Shannon entropy function available on the Protein Variability Server (http://imed.med.ucm.es/PVS). From the alignment file, Shannon entropy is calculated as

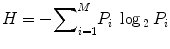$H=-{\displaystyle \sum}_{i=1}^M{P}_i\; \log {}_{2\;}{P}_i$

where P _iis the fraction of residues of amino acid type i and M is the number of amino acid types.

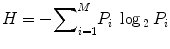
To identify the conserved regions in the L2 capsid proteins of all high-risk HPV strains, the cutoff score for the Shannon entropy was set to 2.0 (Fig. 23.4). The fragments with Shannon variability score ≤2.0 and continuous length of ≥9 amino acid residues were further selected for the epitope identification.

Fig. 23.4

Figure showing the Shannon variability score of individual positions in the multiple alignment files of L2 capsid protein from high-risk HPV strains. Red bars indicate the variability score of amino acid residue i at the given position in the multiple alignment file. Blue line represents the cutoff Shannon variability score. All the red bars below the blue line are potential conserved sites for analysis

Prediction of MHC Class-I and Class-II Epitopes

Epitope mapping is always the key step in vaccine designing. Epitopes are usually thought to be derived from nonself protein Ag that interacts with Abs or T-cell receptors thereby activating an immune response. Besides nonself proteins, epitopic sequences from the host can also be recognized by MHC molecules. For an effective vaccine, it is important for the epitopes to invoke strong response from T and B cells. A large number of bioinformatics algorithms were designed for this purpose, such as Position-Specific Scoring Matrix (PSSM)-based SYFPEITHI [48], Artificial Neural Networks (ANN) [49], Stabilized Matrix Method (SMM) [50], and Average Relative Binding (ARB) [51]. In this work, we used the RANKPEP server (http://imed.med.ucm.es/Tools/rankpep.html) for the prediction of consensus binding epitopes (9 mers) for both MHC class-I and class-II molecules with default parameters. In total, we used 75 MHC class-I and 49 for MHC class-II matrices for the prediction of potential epitopes from all the consensus L2 capsid proteins.

Reverse Translation of Immunogenic Peptide Fragments

To back-translate a peptide sequence into the DNA sequence, a large number of bioinformatics tools are available in the public domain. Because of the degeneracy of the genetic code, the back-translation is ambiguous as most amino acid residues are encoded by multiple codons. To design an optimal DNA sequence, most of these tools use a codon frequency table specific for the organism of interest. We used Backtranseq program of mEMBOSS 6.0.1 for this purpose.

Optimization of Codons and CpG Motifs

Codon optimization is the process to enhance the efficiency of DNA expression vector to express the foreign gene in the host’s cell environment. DyNAVacS server (http://miracle.igib.res.in/dynavac) was used to compute the optimal codon for each of the amino acid residue encoded by the stretch of DNA. The server optimizes codons according to the codon usage table derived from the Kazusa Codon Usage Database (http://kazusa.or.jp/codon). We used a codon frequency table for Homo sapiens that ranks codons by analyzing their frequency of occurrence in 93,487 coding sequences [52]. Immunogenicity of Ag-specific DNA vaccine was previously shown to significantly increase by the optimization of CpG motifs [53]. We again used the DyNAVacs server for CpG optimization [54]. In this process, the consensus motif XCGY (where X is any base but C and Y is any base but G) was incorporated in the sequence as triplet (XCG or CGY) by substituting the less frequent codons that codes the same amino acid residues.

Insertion of Cleavage Motifs and Finalization of DNA Sequence

For the purpose of generating specific epitopes, proteasomal and lysosomal cleavage motifs were also included before and after each MHC class-I and class-II epitope, respectively. These cleavage motifs are targeted by the proteasomal and lysosomal cleavage machineries to generate immune responses in the host. The corresponding nucleotide sequence of the 12-residue long peptide HEYGAEALERAG was added as proteosomal cleavage motif before and after the optimized DNA sequence of each MHC class-I epitope. The HEYGAEALERAG motif contains all five cleavage sites Y3-G4, A5-E6, A7-L8, L8-E9, and R10-A11 defined for eukaryotic proteasomes in which A5-E6 is the major cleavage site [55]. Similarly, the nucleotide sequence of the 5-residue long peptide KFERQ was added as lysosomal cleave motif before and after the DNA sequence of each MHC class-II epitope. KFERQ specifically acts as a recognition motif toward heat shock proteins and facilitates further steps for the degradation of proteins by lysosomes [56] to generate MHC class-II epitopes. At the end, start and stop codons were added to finalize the DNA vaccine. Arrangement of the epitopes is very crucial and one of the deterministic factors for the efficacy of the DNA vaccine. The folding of the protein product in the host will largely depend on the arrangement of these epitopes and also determine the solvent accessibility of the cleavage motifs. Various computational tools can be used for this purpose including molecular dynamics simulation approaches. The overall arrangement of the DNA vaccine construct is shown in Fig. 23.5.

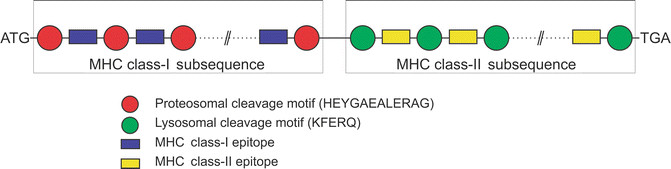
Fig. 23.5

Arrangement of various segments of DNA vaccine constructs. The arrangement of epitopes in the sequence is very crucial to increase the efficacy of DNA vaccine

In Silico Cloning Experiments of DNA Vaccine Construct

Several expression systems have been successfully designed in the past, for the cloning of the number of genes encoding surface antigens from pathogens to facilitate vaccine development. A good DNA vaccine vector should be designed with minimal functions so that the only gene expressed in mammalian cells is the antigen-encoding gene. We performed the cloning experiments using clc-DNA Workbench 5.0.1. For our purpose, the pVAX1 vector was selected as an expression system. pVAX1 is a nonfusion vector specifically designed to stimulate cellular as well as humoral immune responses [57] and requires that the inserted gene of interest contains the Kozak translation initiation sequence, an initiation codon (ATG), and a termination codon (TAA, TGA, or TAG). When this designed DNA vaccine is injected into the host, the antigenic protein gets translated and alerts the body’s immune system to generate immunization memory cells.

The methodology described above highlights how various bioinformatics algorithms and computational tools can be combined to design novel and effective vaccine candidates before being subjected to in vitro confirmatory studies.

23.4.2 Mathematical Models Used in Basic Oncology Research

23.4.2.1 Pathways and Networks

The successful use of systems biology to elucidate the regulation and function of cancer-related pathways is well proved by a large body of literature published in the last decade. In this context, mathematical modeling has been used to investigate the time-dependent behavior of biochemical systems, to integrate multiple data sources, or to validate the existence of new regulatory or transcriptional interactions in given regulatory pathways. A question in biochemical networks for which data-driven mathematical modeling is necessary is the elucidation of the nonlinear properties emerging from the combination of regulatory motifs containing positive/negative feedback and coherent/incoherent feedforward loops. When biochemical pathways or networks hold these regulatory structures, they often display behavior that evades direct reasoning. Many papers, which use a data-driven modeling approach, succeeded proving how signal amplification [11], sustained oscillations [58], or bistability [59] emerged as hallmarks of signaling and transcriptional networks.

To mention an example on immune-related pathways, Das and colleagues [60] integrated different modeling approaches with in vitro experiments to elucidate the interplay between Ras activation and SOS proteins in the activation of T and B lymphocytes. What makes their work interesting is that both proteins, Ras and SOS, are integrated in a positive feedback loop that participates in the Ag receptor stimulation of lymphocytes. In this feedback loop, Ras gets strongly activated upon membrane receptor stimulation, a process which is mediated by members of the SOS family. In turn, SOS activity at the plasma membrane is allosterically upregulated by active RasGTP. To validate the existence of this positive feedback loop and its functional consequences, the authors combined model simulations and time-dependent in vitro experiments with human and chicken lymphocytic cell lines. They found that under some stimulatory conditions, the biochemical system displays bistability. That is, for high doses of stimulus, the pathway works like an all-or-nothing system: transient but intense stimulus can trigger a sustained activation of the system and the downstream pathway. When we consider a population of lymphocytes, this property may induce the emergence of a bimodal response, with a subpopulation of lymphocytes getting full and sustained activation, while others remain inactive. From an immunological perspective, the authors hypothesize that this system induces the emergence of a short-term mechanism of molecular memory. This mechanism can improve the activation of T lymphocytes which were stimulated in previous serial encounters with rare antigen-bearing cells.

In the study by Das et al. [60] the focus was to elucidate the dynamics of a small signaling system containing regulatory loops. In other cases one tries to address how several pathways cross talk to each other and integrate their signals to achieve the regulation of given phenotypic responses. This has also been explored using mathematical models of large regulatory networks in the context of cancer [61] and immunology [62]. For example, Carbo and collaborators [63] used a systems biology approach to investigate the regulation of the pathways underlying CD4⁺ T-cell differentiation. By collecting and organizing the state of the art of biomedical knowledge, they constructed a comprehensive regulatory map of the critical pathways regulating the differentiation of naïve CD4⁺ T lymphocytes into Th1, Th2, Th17, or iTreg. The regulatory map was translated into a mathematical model in ordinary differential equations and characterized using perturbation experiments, in which different concentrations of relevant cytokines were used to stimulate the shift between different signaling and transcriptional pathways and therefore the distinctive differentiation of the naïve T cells. Once the model was calibrated and validated, model simulations and sensitivity analysis were combined to determine the model parameters controlling the activation of different pathways. They found that the pathway regulating the nuclear receptor PPARc function plays a major role controlling the shift between the Th17 and iTreg transcriptional and phenotypic programs. Based on these findings, they foresee a therapeutic potential to the regulation of PPARc signaling in the context of chronic inflammatory and infectious diseases. In this way, the authors show how a full systems biology strategy can be extremely useful to dissect the signaling and transcriptional networks controlling differentiation and plasticity of immune cells.

23.4.2.2 Genotype-Phenotype Mapping

Mathematical models can be used to bridge the gap between intracellular pathways and the cellular phenotypes they regulate. In this case, the idea is to develop mathematical models that consider how genetic or epigenetic changes in critical cancer-related pathways can affect the fate of tumor cells and trigger (or disrupt) phenotypic responses at the cellular level. Some authors call this the genotype-phenotype mapping [64].

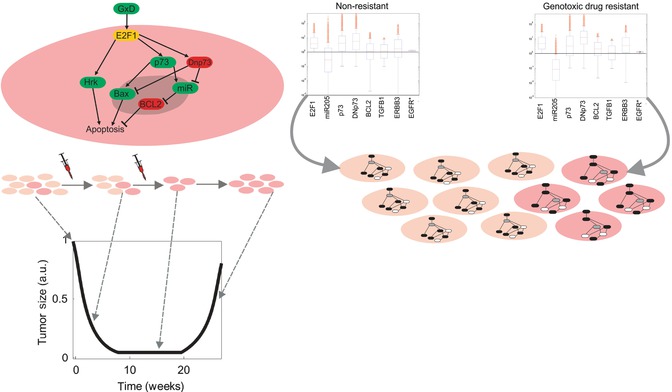
We have recently applied this idea to investigate the deregulation of critical cancer signaling-transcriptional networks during the emergence of a phenotype of chemoresistance ([8], see Fig. 23.6). To this end, we constructed a data-driven mathematical model in ordinary differential equations (ODEs) accounting for an intracellular network around E2F1, a transcription factor involved in abnormal cell proliferation, apoptosis, and chemoresistance. The network included the interaction of E2F1 with two isoforms of p73 and the microRNA miR-205, as well as a number of transcriptional targets whose regulation after anticancer drug administration is controlled by these E2F1/p73/miR-205 networks. To make the genotype-phenotype mapping possible, we connected our model with an additional equation that describes the size of a population of tumor cells whose response upon stimulation with anticancer drugs was controlled by the E2F1-centered network. In this equation, basic phenotypic traits of the modeled cells like proliferation or death rate were connected and therefore controlled by the E2F1-regulated transcriptional targets. These transcriptional targets represent the triggering of proliferative, apoptotic, or antiapoptotic programs in the model.