Biomechanics
Frederick W. Werner
Joseph A. Spadaro
Some Basic Biomechanical Terms
Force (load): A force is an action on a body. It has a direction and a magnitude.
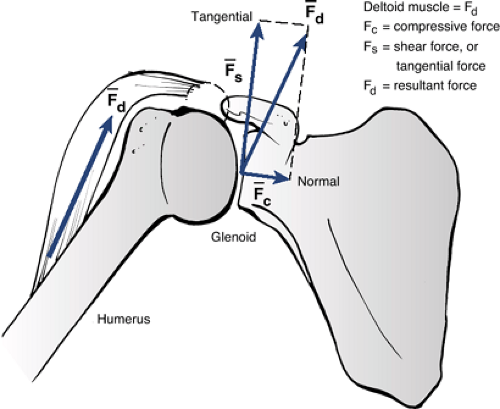
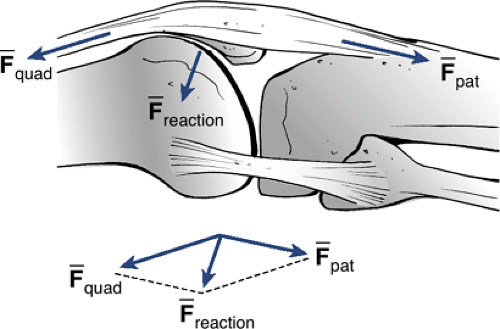
Oblique forces: A force being applied at some angle to a coordinate system can be represented as two perpendicular or orthogonal forces in that coordinate system.
Magnitude of the oblique force on the implant is the square root of the sum of the squares of the perpendicular forces (Fig. 16-1).
Graphically, the force on the implant is the hypotenuse of the right triangle formed by the perpendicular forces.

Figure 16-1 Vector addition of two orthogonal forces to obtain the force, F. A force is represented by drawing either an arrow or line over the letter corresponding to that force.
Dynamic forces: Dynamic forces include the effect of the inertia of the person moving or an impact on an object against another.
Example of normal walking gait: During gait, the forces on the knee joint are due to the weight of the person, the muscles causing the knee to move, the ligamentous structures that provide stability, and the inertia of the person as the heel strikes the floor and as he or she pushes off before toe off.
Moment: A moment is defined as a force being applied at some distance away from some pivot point. Its magnitude is the force times the moment arm.
Moment calculation: If several moments are being applied to a bone or some object in equilibrium, then the sum of those moments about a given point is equal to zero.
Torques: A torque is typically caused by a twisting motion such as opening ajar. There is an equal but opposite torque required to resist the torque being applied to open the jar.
Torque = applied force × the moment arm
Units: Forces are typically measured in Newtons (N). Moments and torques are measured in Newton-meters (N-m) or Newton-millimeters (N-mm).
Kinematics
Kinematics is the study of how things move. Motions can be viewed as displacements (translations), as rotations, or as a combination of them. A person or object might be moving at a constant velocity or with a changing velocity, in which case it is accelerating or decelerating.
Velocity: The rate (speed) and direction of movement of an object, such as a car moving down the road. The magnitude of the velocity is the distance or displacement of the object per unit time.
Acceleration and deceleration: If the speed of that object, or its direction, is changing, then the object is either accelerating or decelerating.
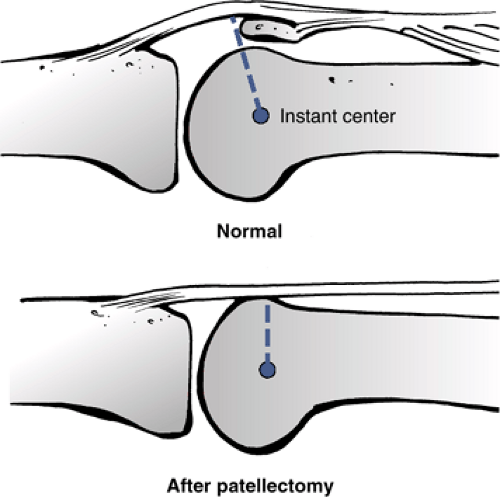
Center of rotation: For most joints in the body, one can find a center of rotation about which the bone is rotating. For example, door hinges are the fixed center of rotation for a rotating door. In the knee joint and many others, the center of rotation is not fixed but changes through the range of knee flexion.
3D center of rotation: In the knee joint as well as in other joints in the body, the motion is not necessarily planar. As the knee flexes and extends, tibial rotation and ab/adduction cause the center of rotation to move in three dimensions.
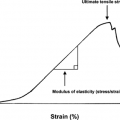
Mechanical Properties of Materials
Stress: A force applied to an implant or bone will cause a stress in the material.
Stress = applied force divided by the area over which the force is being applied (typical units are N/mm2)
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree