Introduction
The potential of physical characteristics of protons for cancer treatments was first recognized by Wilson in 1946. During the following four decades or so, proton accelerators at various physics laboratories around the world were adapted for clinical purposes. Examples of such facilities include the University of California Berkeley; the Harvard Cyclotron Laboratory in Cambridge, Massachusetts; Uppsala University, Sweden; Dubna, Russia; and Chiba, Japan. Physics laboratory-based particle therapy facilities are designed for physics applications and, as such, are not suitable for clinical applications. This led to the establishment of hospital-based proton therapy facilities. The first among these was at the Loma Linda University Medical Center, California, in 1990, followed by Massachusetts General Hospital-Harvard University in 1999, the MD Anderson Cancer Center (MDACC) in Houston, and the University of Florida in Jacksonville, both in 2006. Since then, the number of proton therapy centers in the United States and around the world has grown dramatically. According to the Particle Therapy Co-Operative Group (PTCOG) website ( http://www.ptcog.ch ), as of March 2018, there were approximately 27 proton therapy facilities in operation in the United States and nearly 70 around the world. As of December 2016, 150,000 patients worldwide had been treated with protons.
Along with the rapid growth in the number of proton centers, the technology has continued to evolve. Whereas up until the last decade most of the proton treatments were carried out using passively scattered beams, the new treatment centers are now being equipped almost exclusively with scanning beam systems. These systems provide much greater flexibility to optimally shape dose distributions. Accelerators and gantries continue to become more compact and have greater functionality and lower cost. The treatment delivery control systems are becoming more sophisticated, allowing proton therapy systems to deliver superior treatments more efficiently.
Furthermore, ongoing research over the last dozen years is resulting in improved understanding of the sensitivity of protons to inter- and intrafractional anatomy variations, range uncertainties, setup uncertainties, and the unique biological effects of protons. This knowledge is being incorporated into the development of intensity-modulated proton therapy (IMPT) methods to optimize biologically effective proton dose distributions to achieve higher and higher therapeutic ratios. Accuracy of dose distributions is being improved with the introduction of Monte Carlo techniques and made practical with the development of fast Monte Carlo methods. Clinical trials, many of them randomized protons versus photons, are being conducted to evaluate the relative clinical and cost-effectiveness of protons.
In principle, protons have a much greater therapeutic potential than has been realized to date. Although the technology has improved substantially and we have made significant strides in improving our understanding of physical, biological, and clinical aspects of proton therapy in the recent past, considerable additional research and development are needed to maximally exploit the potential of proton therapy. Sections later describe the principles underlying proton therapy, the current state of the art and its limitations, ongoing research and development to advance the state of the art, and the long-term promise of radiotherapy with protons.
Physical characteristics of protons
The rationale for the use of protons to treat cancers is built upon their unique physical characteristics. These characteristics allow the production of radiation dose distribution patterns that conform more tightly to the shape of the tumor target and avoid normal tissues to a greater extent. The physical characteristics of protons also lead to biological effects that are, in general, quite different from those of the traditional radiation treatment modalities. Taken together, the physical and biological properties of protons offer a substantially higher therapeutic ratio.
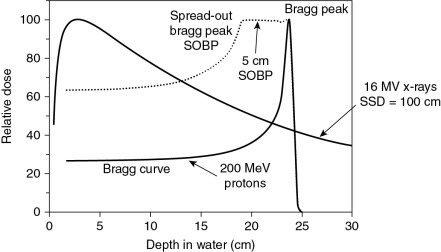
Protons interact with matter primarily through Coulomb interactions with atomic electrons, Coulomb interactions with nuclei, and nuclear interactions. As a proton traverses the medium, it slows down continuously. The energy deposited by it per unit distance (called the linear energy transfer, or LET) increases until all of its energy is depleted, and it comes to essentially an abrupt stop. Thus, in a uniform medium, for example, a water phantom, a monoenergetic beam of protons leads to the formation of the characteristic Bragg curve ( Fig. 2.1 ). Because protons are much heavier than electrons, Coulomb interactions with electrons do not deflect them appreciably from their original path. However, Coulomb scattering from nuclei, although it occurs much less frequently, leads to larger-angle scattering and contributes to a substantial lateral spreading of proton beams. It leads to the widening of proton beam penumbra, especially when the protons have slowed down near the end of their range. Interactions of protons with nuclei occur with even lower probability and mainly at higher energies and lead to large-angle scattering and the production of secondary particles, including neutrons.
These properties of protons have a profound impact on the biological and clinical effects. Protons ionize more densely than photons. The density of ionization increases with increasing LET as they slow down as a function of depth. This, in turn, causes continuously increasing biological damage (e.g., more complex and clustered DNA damage), thus continuously increasing relative biological effectiveness (RBE) as a function of depth. The RBE is a complex function with physical and biological parameters. It is briefly dealt with in the section on Proton Biological Characteristics. More details can be found in Chapter 1 and in the literature, including some cited at the end of this chapter. The variations in RBE can be exploited to enhance the biologically effective dose differential between the target and normal tissues.
In addition, protons have a lower entrance dose compared with photons (except in the entrance buildup region, see Fig. 2.1 ) and virtually no dose beyond the end of their range. Thus theoretically, they can be used to produce considerably more “compact” dose distributions (smaller “low-dose bath”). Such dose distributions can, in general, spare large volumes of normal tissues for the same target dose (see the section on Proton Therapy Planning and Plan Evaluation and Chapter 5 for more details.). Recent recognition of additional value of such compact dose distributions is their potential to mitigate radiation-induced lymphopenia (RIL), which is widely recognized to be a significant prognostic indicator of adverse outcomes.
It should be noted that although sharp falloff of dose at the end of the range of protons is critical to the improved patterns of dose distributions, it also has potential negative ramifications. It renders proton dose distributions, compared with photon dose distributions, more vulnerable to intrafractional changes in anatomy due respiratory motion and other physiological functions, and to interfractional variations in anatomy because of such factors as weight gain or loss, tumor shrinkage, setup variations, and so on. Special efforts are required to minimize uncertainties thus introduced and to address residual uncertainties.
Proton biological characteristics
A common misconception about proton therapy is an inherent assumption that, for the same physical dose delivered to a tissue, the biological and clinical effects of protons and photons are identical except that protons are 10% more biologically effective. In other words, the RBE of protons is a constant of 1.1. In reality, as protons interact with the tissues in the body (and matter in general), they traverse very differently and in a more complex manner. As a consequence, they have very different biological and clinical effects. They should be considered a different form of drug, perhaps many different forms of drug, depending on their physical parameters and the dose delivered. It is crucial that practitioners of proton therapy understand and appreciate these differences to apply proton therapy more effectively.
Biological effects in the current practice of proton therapy
Appropriately, the clinical practice of proton therapy is based on our vast clinical experience with photon therapy. Such extrapolation requires that we understand the biological effects of the protons relative to photons. Extensive in vitro and in vivo studies have been carried out in the past to measure the biological effectiveness of protons relative to photon irradiation (i.e., the RBE). Paganetti et al. have summarized these data in two articles. , They argued that, considering uncertainties in the data, the use of an average value would be appropriate. In the current practice of proton therapy, the proton RBE is simplistically assumed to be a constant of 1.1 for all tumors and tissues, independent of dose and LET. However, the past experiments, the foundation of RBE of 1.1, were carried out under a broad range of inconsistent and underreported conditions and had large uncertainties in the results. Most of these experiments were conducted at high doses per fraction (5–8 Gy) and at points in the middle of large (∼10 cm), spread-out Bragg peaks (SOBPs) of relatively high-energy protons. Moreover, the data were measured for only for a relatively small number of cell lines, tissues, and end points. Thus, it is not surprising that most of them yielded a value in the neighborhood of 1.1.
It is increasingly being recognized now that RBE is variable and a complex nonlinear function of dose per fraction, LET, tissue and cell properties, and other factors. Ignoring such variability may have a significant adverse impact on outcomes and could limit the effectiveness of proton therapy. Nevertheless, the RBE of 1.1 continues to be used clinically. To justify this practice, many have argued that no adverse responses have been reported attributable to this choice. However, “absence of evidence is not evidence of absence” of the effect. It is quite plausible that uncertainties in treatment planning and delivery processes could have masked the effect. As more and more patients are treated, unforeseen recurrences and toxicities are now being reported. Among them is the report of Gunther et al., who compared rates of postradiotherapy changes in magnetic resonance (MR) images in pediatric ependymoma patients treated with photon and proton therapy. They found that a greater proportion of proton therapy patients versus IMRT patients (43% vs. 17%) developed postradiation MRI changes and at earlier times (3.8 months [median] vs. 5.3 months [median]). The grade and incidence of image intensity changes were also greater for protons than for photons. Other examples include reports of Weber et al. and Mizumoto et al., who have reported serious neurological toxicities for patients treated with proton therapy.
Although there may be multiple contributing factors involved in such failures, the assumption of RBE of 1.1 may be among the important ones. The remedy chosen, applicable mainly to passively scattered proton therapy (PSPT), has been to avoid beam directions pointing toward the critical normal structures, such as brain stem or spinal cord, or to block the protons from reaching the critical structure. These approaches are ineffective for IMPT because the dose distributions per beam are highly heterogeneous. Another approach used has been to reduce the prescription dose. For instance, realizing the potential for increased brainstem necrosis, which can have profound clinical consequences, Indelicato et al. have opted to reduce the prescription doses.
Laboratory and clinical studies to quantify proton biological effects accurately
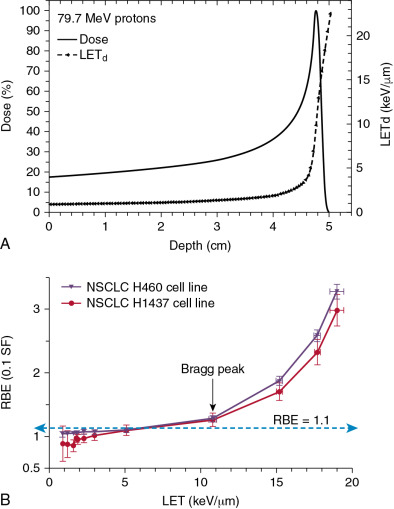
Realizing the large gaps in knowledge of the biological effects of protons, multiple efforts are being mounted to conduct high-precision, high-accuracy in vitro and in vivo experiments. Examples of the studies already published include the works of Guan et al., Chaudhary et al., , and Liu et al. , Guan et al., for instance, using specialized equipment designed using Monte Carlo simulations and scanning monoenergetic proton beams, showed that RBE varies substantially, especially around the Bragg peak, reaching values of up to 3 or 4 in the distal falloff region ( Fig. 2.2 ). Chaudhary et al. reported similar behavior for different cell lines. In addition, Liu et al. , showed that, for a set of 17 different lung cancer cell lines, the RBE deviates substantially from 1.1, even in the middle of the SOBP. They attributed their findings to, in part, Fanconi anemia/Breast Cancer gene (BRCA) pathway defects. Interestingly, although the dose-averaged LET value in the middle of the SOBP is low, there is a wide spectrum of energies and LET values at mid-SOBP. It is plausible that using dose-averaged LET as a surrogate of biological effect is not warranted. In general, proton biology is more complex, and continued further investigations are needed. (More details may be found in Chapter 1 .)
Deducing proton relative biological effectiveness from clinical response
Translating laboratory in vitro and in vivo data directly into clinical practice, especially because most of the data are for clonogenic cell survival, is questionable. One could attempt to deduce it from the proton versus photon clinical response data. Unfortunately, data available are insufficient and have a high degree of uncertainty, which is likely to obscure the real properties of RBE. Nevertheless, it would be useful to refine the laboratory data–based models to fit clinical response differences between protons and photons. For instance, one may fit a normal tissue complication probability model to photon data and proton data separately. The differences in the model fits may be attributable to RBE. Then, assuming dose distributions for both protons and photons are calculated accurately (e.g., using Monte Carlo techniques), the RBE model parameters may be adjusted (optimized) so that they fit proton and photon data fit simultaneously.
Using a different approach, Peeler et al. analyzed the data of Gunther et al. mentioned earlier to determine if the pre- and postradiotherapy image changes were associated with higher LET and hence attributed to a deviation of proton RBE from 1.1. They showed that the probability of image change is a function of dose as well as LET and that the dose for 50% probability of change in image voxel intensity is a function of LET. Their results suggest that increased LET contributes to a higher incidence of imaging changes within the brain tissue, indicative of radiation damage with increasing RBE. Extracting RBE from treatment response data, although challenging, is more clinically relevant.
Modeling of proton biological effects
Improved knowledge of RBE could be used to enhance optimality and clinical effectiveness of treatment plans. This can be realized most suitably using IMPT, which affords the highest degree of control over achievable dose distribution patterns. Predictive RBE models may be incorporated into the criteria of optimization of IMPT dose distributions to direct higher RBE protons into the target volume and away from normal tissues. RBE models may also be used to compute biological effects to evaluate given dose distributions to aid in clinical decision making. Such models can also be highly valuable in comparing competing treatment plans as well as proton dose distributions with photon dose distributions. Numerous models to predict RBE have been published. However, they tend to be simplistic, assuming that RBE is a linear function of dose-averaged LET, and do not adequately fit most recently published radiobiology data. Research is taking place to develop novel models and to improve the accuracy of the current models to predict RBE. For further discussion of RBE models, the reader is referred to an article by Mohan et al. and to references cited earlier.
Proton therapy delivery system
For clinical applications, protons are accelerated with cyclotrons or synchrotrons to therapeutically relevant energies, typically from 70 to 250 MeV. The energy or the sequence of energies needed are determined by the minimum and maximum depths of penetration required to irradiate the target volume.
An accelerated proton beam entering the treatment delivery head (i.e., the “nozzle”) is very thin and has depth dose characteristics shown as the Bragg curve in Fig. 2.1 . As such, it is not suitable for treating three-dimensional, arbitrarily shaped tumor targets. It must be broadened longitudinally and laterally and shaped to conform to the target shape. There are two main approaches to achieve this: (1) passive scattering to deliver PSPT, and (2) magnetic scanning of “beamlets” of protons of a sequence of initial energies to deliver IMPT. The latter is much more powerful technique to produce desired patterns of dose distributions. As mentioned, most of the treatments with protons to date have employed PSPT. However, nearly all the new installations are now based on scanning beam technology.
Proton accelerators
In general, protons for radiotherapy applications are accelerated using cyclotrons or synchrotrons; each type has advantages and disadvantages. Cyclotrons produce a continuous stream of protons. In theory, they are more compact and have higher beam intensity. Protons are accelerated to the maximum of the energy of the cyclotron (e.g., 230 MeV), and the required lower energies are achieved by electromechanically inserting energy degraders in the path of protons. Synchrotrons, on the other hand, accelerate batches of protons to the desired energy. Once a batch has reached the required energy, it is extracted and transmitted via the “beam line” to the treatment room. The extraction may occur over a variable period of time from 0.5 to 4.5 seconds or longer, depending on the application. An additional 1 to 2 seconds are required to allow for resetting of the acceleration system between extractions and changing energy. Generally, the advantages of synchrotrons include greater energy flexibility, smaller energy spread, and lower power consumption. Regardless of the acceleration mechanism, the extracted narrow monoenergetic beam is magnetically guided through the beam line to the treatment room into the nozzle mounted, in most cases, on a rotating gantry. At most treatment facilities, a single accelerator serves multiple rooms. However, vendors are now offering single-room systems.
In typical scanning beam treatments with synchrotrons, depending on the depth of the target, a large number (∼20−50) of energy layers may need to be scanned. If a field is large, multiple cycles may be required for the same energy layer, and for small fields, unused protons may be discarded. Considering that each cycle takes about 6 seconds or more, including the change in energy, the total time to deliver a fraction may be quite long. Newer systems are being designed to have higher dose rates and faster energy changes. Moreover, they permit multienergy extraction in which the energy is reduced from a maximum in a series of steps to allow scanning along the depth of the target.
For scanning beam treatments with cyclotrons, the energies of scanning beams from energy layer to energy layer are changed using high-precision movements of a fast energy degrader.
Passively scattered proton therapy
For PSPT, the lateral and longitudinal spreading of the thin beam entering the nozzle is achieved with a combination of a rotating modulation wheel and one or two scatterers. This combination produces a SOBP, a uniform, cylindrically shaped dose distribution with a relatively low dose proximally and a rapidly falling dose distally. To conform the dose distribution laterally to the shape of the target volume, an aperture, typically made from blocks of brass of sufficient thickness (2−8 cm) to absorb incident protons of the highest energy, is used. To create a dose distribution that conforms to the distal shape of the target, the SOBP is shaped further by using a range compensator made of a nearly water-equivalent material. Because the SOBP width for a passively scattered beam is designed to be constant across the entire field, passive scattering provides no control over dose distribution proximal to the target. For a target with a highly irregular distal edge, this may lead to a substantial excess volume of high dose proximal to the target.
Scanning beams
A considerably clinically more effective approach is to shape the beams using magnetic scanning of thin beamlets of protons. Multiple beams incident from different directions, each comprising the scanning beamlets of sequences of energies, may be used to produce the desired pattern of dose.
Protons in a beamlet incident on a patient or a phantom are very nearly monoenergetic and are distributed essentially as a narrow Gaussian function of position relative to the beamlet’s central axis. The lateral dimension of a beamlet is expressed in terms of the full width at half maximum (FWHM) of the Gaussian, or its σ. A smaller FWHM is desirable because it allows for a sharper penumbra and a greater control over dose distributions. In air, higher-energy proton pencil beams have a smaller FWHM than the lower-energy ones. Typically, the smallest achievable FWHMs in air for the highest energies (220−250 MeV) range from 7 to 12 mm (or σ of 3–5 mm), depending on the vendor and the machine model. Once the pencil beam enters a medium, such as a phantom or a patient, the FWHM increases substantially, especially near the end of the range of protons.
Magnetic scanning of beamlets provides greater flexibility and control for creating the optimum conformal proton dose distribution. In addition, the elimination of mechanical shaping devices (such as apertures and compensators) saves the cost of fabricating them and the time required for the insertion of these devices, obviates the need to enter the treatment room between fields, and makes the treatments more efficient. Most importantly, scanned techniques allow the delivery of IMPT, potentially the most effective form of proton therapy. The positions and intensities (in terms of monitor units) for a matrix of spots within the target volume for each scanned beam are determined by the treatment planning system to achieve the acceptable or the best possible approximation of the desired dose distribution.
Proton scanning beams have been in use for patient treatments at the Paul Scherrer Institute since 1996, where a one-dimensional scanning of proton pencil beams of different energies in the patient’s transverse plane is used. The other dimension is achieved by moving the couch along the patient’s longitudinal axis. The first use of two-dimensional scanning occurred in May 2008 at MDACC, where it is now used routinely. Recognizing the potential of scanning beams, most new proton therapy installations primarily or entirely employ scanning beams. Further research and development of this technology are continuing.
For scanning beams, proximal and lateral field shaping is achieved by limiting the positions of the spots to within the target regions only. Presumably, there is no need for an aperture. However, because of the substantial size of the pencil beam spots, consideration is now being given to the use of dynamic apertures that can change their shapes layer by layer.
More details on treatment delivery issues may be found in Chapter 6 .
Proton therapy planning and plan evaluation
These issues are discussed in detail in Chapter 5 . However, some comments are in order and may be helpful in appreciating the differences in processes and techniques for protons and photons. Planning and evaluation also often require different types of tools.
We reiterate the statement that protons are more sensitive to intrafractional anatomy motion, interfractional anatomy changes, and setup variations. Moreover, although they have a finite range and a rapid dose falloff at the end of the range, there is uncertainty in range, which is a function of depth of penetration. In addition, heterogeneities in the path of protons and their shifts relative to the beam direction perturb dose distributions in the tumor in a complex manner. On the other hand, rigid shifts in patient position along the beam direction have virtually no impact on dose distribution. Thus, the traditional concept of PTV margin for photon therapy to ensure that the clinical target volume (CTV), in the face of uncertainties, receives the prescribed dose with high probability does not apply to the beam direction. The solution applied for PSPT is to assign margins to distal and proximal edges of the tumor along each beam’s direction to design the target volume. Further, to mitigate the perturbation of dose within the tumor, the compensator used to conform the dose distribution to the distal edge of the target is “smeared.” Such solutions are not applicable for IMPT. In IMPT, dose distributions in the target for each of a group of beams are highly heterogeneous, which match with each other in a way that there is a homogeneous dose distribution. The perturbations caused by sources of physical uncertainties lead to a loss of match and, therefore, to heterogeneity in the target dose.
For both PSPT and IMPT, respiratory motion is accounted for by defining an internal motion-incorporated volume, and dose distributions are computed assuming the body to be a rigid representation of the average of phases of four-dimensional computed tomography (4D CT). In common with photon therapy, it is further assumed that, if the tumor motion is less than a certain threshold (e.g., 5 mm), there is no need for any special motion management intervention, such as breathhold or respiratory gating. In fact, it has been shown that the perturbation of dose distribution depends not just on tumor motion but also on the respiration-induced changes in the path of protons. Thus the decision regarding whether to use special motion management steps should be based on changes in dose distribution over the breathing cycle, for instance, from end-inhale to end-exhale.
Uncertainties mentioned in the paragraphs above mean that the dose distribution actually received by the patient is different from what a clinician sees on the treatment plan and uses to make treatment decisions. Such differences are greater for protons than for photons. Solutions to address this problem have been developed in the recent past and are being implemented in commercial treatment planning systems. Among them is robust evaluation of treatment plans to assess their resilience in the face of uncertainties. Dose distributions are recalculated for a set of expected uncertainty scenarios, and bands of dose-volume histograms (DVHs) for all scenarios are graphed and used to assess the suitability of a plan. Often, the “worst-case” scenario for the CTV coverage is chosen because it corresponds to the use of planning target volume (PTV) for photons. Note that PTV is meant to ensure that the CTV is covered with a prescribed dose with high probability. In other words, the PTV DVH represents the worst-case DVH for the CTV. Robustness evaluation is applicable to both PSPT and IMPT. It is also applicable to photons but generally is not considered necessary.
For IMPT, it also possible to render dose distributions as less sensitive uncertainties by using a process called robust optimization, in which the intensities of beamlets are optimized to maximize the probability of CTV coverage and normal tissue sparing under all uncertainties simultaneously. For IMPT of disease sites affected by respiratory motion, 4D robust optimization is a solution. In it, IMPT is optimized to achieve the desired tumor and normal tissue constraints simultaneously for all uncertainty scenarios as well as for all respiratory phases.
Although robustness evaluation and robust optimization make dose distributions more reliable in terms of what a patient receives, they do not necessarily improve the optimality of the plan. In fact, making robustness requirements more stringent in robust optimization may degrade the optimality. Thus it is important to reduce uncertainties using such techniques as in-room volumetric imaging for treatment setup and more frequent adaptive replanning to account for interfractional anatomy changes. Another source of uncertainty for proton therapy is the approximations in computed dose distributions. It is important that the CT images used for dose calculations be obtained with dual-energy CTs, which have reduced artifacts and provide image data that can be converted more accurately to stopping power ratios, the quantities that are required for proton dose calculations. Moreover, the analytic proton dose calculation models implemented in commercial treatment planning systems are inadequate, and it is necessary to resort to Monte Carlo systems or their faster versions being developed. Monte Carlo systems are also more appropriate for computing proton LET values and energy spectra needed for computing variable RBE values.
Although many of the steps mentioned may also be useful for photons, they are essential for protons.
Incorporating variable relative biological effectiveness in evaluating and optimizing proton dose distributions
As emphasized previously, a unique aspect of protons is their biological properties. The proton RBE models being developed can be used to calculate biologically effective (RBE-weighted) dose distributions. Such dose distributions may be particularly useful to assess whether the variable RBE might have played a role in unforeseen toxicity or local failure. However, it is essential that, to isolate the biological effect that may be responsible, uncertainty in computed dose distributions need to be minimized to the extent possible.
RBE models may also be incorporated into IMPT optimization criteria to, in principle, produce a higher biologically effective dose within the target and lower within the surrounding normal tissues. Note that the primary rationale for using protons is their characteristic Bragg curve. Because the variable RBE-weighted dose at the Bragg peak is 30% to 40% higher than the entrance dose compared with the physical dose, it would seem that the incorporation of variable RBE into the IMPT optimization criteria may lead to a greater differential between target and normal tissue doses compared with the use of a constant RBE of 1.1. However, there has been some resistance to the use of variable RBE models for this purpose, citing uncertainty in the models as the reason. This is true; however, it can be argued that even the rudimentary models would lead to superior biologically effective dose distributions compared with the assumption of RBE of 1.1.
An alternative strategy has been proposed to include terms based on LET in the optimization criteria to push the LET to higher levels in the target volume to lower levels in normal tissues. , The rationale is that LET distributions can be calculated accurately. However, LET may not be an adequate surrogate of biological effect, and, ultimately, accurate RBE models will need to be incorporated ( Fig. 2.3 ).