Clinical commissioning of pencil beam scanning for intensity-modulated proton therapy

Introduction

In radiation oncology, “clinical commissioning,” or simply “commissioning,” refers to the process that takes place after a machine has passed acceptance tests but before the first patient can be treated. Commissioning tasks for proton therapy include but are not limited to the following: (1) calibrating the computed tomography (CT) scanner for proton therapy; (2) acquiring beam data and establishing and validating the beam model in the treatment planning system (TPS); (3) commissioning the radiation delivery system, including end-to-end testing with the electronic medical record (EMR) system to be used; (4) building a comprehensive quality assurance program with machine-specific and patient-specific components; (5) establishing a safety program and meeting regulatory requirements; (6) developing operational procedures; and (7) training staff members who will plan and deliver the treatments. ^, Many of these tasks can be started long before the beam becomes available on the machine, including calibrating a CT scanner, evaluating immobilization devices, and training and practice for proton therapy treatment planning. Some vendors also use the term commissioning to describe the process of tuning and adjusting the machine to prepare it for acceptance testing after the equipment is installed; we recommend that this process be referred to as technical commissioning to distinguish it from the subject of this chapter, which is “clinical commissioning.”

The purpose of acceptance testing is to determine if the machine satisfies the contractual and performance specifications and pertinent safety requirements. Acceptance testing can be performed entirely by qualified medical physicists, by vendor representatives, or by some combination of both. However, determining whether the machine is acceptable and ready for clinical commissioning is the responsibility of medical physicists. Because some acceptance and commissioning tests overlap, in such cases, the results of the two sets of tests can be shared to save time. However, the goals of acceptance testing and commissioning are different, and the two processes cannot be combined into one. The focus of this chapter is on steps 1, 2, and 3 from the first paragraph, that is, calibrating the CT numbers (Hounsfield units [HUs]) for proton therapy, establishing and validating the beam model to be used for the TPS, and commissioning the treatment delivery system.

Calibration of computed tomography numbers for proton therapy

As is the case for photon-based radiation therapy, kilovoltage (kV) x-ray CT images are currently used to create models of patients and treatment plans for proton therapy. For photon dose calculations, calibration needs to be established between the CT number and electron density; for proton dose calculations, the CT number is related to the proton stopping power. One common approach used for calibration is the stoichiometric method, ^, the main steps of which are as follows :

1.

Measure the CT numbers of some tissue substitutes of known chemical composition and physical density. (An example of tissue substitute inserts, with their compositions and physical density, is given in table 3.1 of Schneider et al. )
2.

Use linear regression to fit the measured CT numbers of the tissue substitutes to Eq. (3.1) to determine the coefficients, A, B, and C, which characterize the cross-sections for the photoelectric effect, coherent scattering, and incoherent scattering, respectively, of the kV x-ray beam interacting with the phantom and the insert :

????=?????(??˜3.62+??ˆ1.86+?)
H U S C = ρ e r e l ( A Z ˜ 3.62 + B Z ˆ 1.86 + C )
- where HU is the CT number and HU _SC= HU + 1000 is the scaled CT number; ?????
 ρ e r e l
 is the electron density relative to water; ?˜
 Z ~
 =[∑???3.62?]1/3.62
 = [ ∑ λ i Z i 3.62 ] 1 / 3.62
 , ?ˆ=[∑???1.86?]1/1.86,??
 Z ˆ = [ ∑ λ i Z i 1.86 ] 1 / 1.86 , λ i
 , is the fraction of number of electrons per unit volume for element i ; and Z _iis the atomic number of element i . An example of calculated scaled HU versus measured scaled HU is shown in Fig. 3.1 .
 
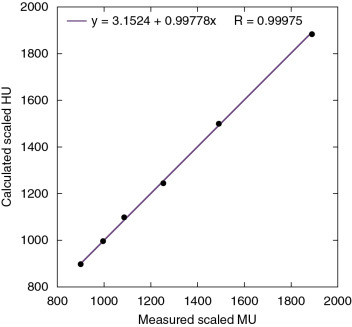
 Fig. 3.1
 
 Example of calculated versus measured scaled Hounsfield units ( HUs, where a scaled HU = HU + 1000) of tissue-substitute materials of known composition and density. MU, Monitor unit.
3.

Compute the CT numbers of various reference tissues as given in the International Commission on Radiological Protection (ICRP) Report 23 by using Eq. (3.1) with the coefficients determined in step 2.
4.

Compute the relative linear stopping power (RLSP) for the same ICRP tissues by using an approximation to the Bethe-Block formula ^,:

????=??????
R L S P = ρ e r e l K
- where ?={log[2???2?2??(1–?2)]–?2}/{log[2???2?2??(1−?2)]–?2},
 K = { log [ 2 m e c 2 β 2 I t ( 1 – β 2 ) ] – β 2 } / { log [ 2 m e c 2 β 2 I w ( 1 – β 2 ) ] – β 2 } ,
 m _eis the mass of electron, c is the speed of light, βc is the speed of the proton, and I ^tand I ^ware the mean ionization potentials of the tissue and water, respectively. Among the physical quantities in Eq. (3.2) , the mean ionization potentials have the largest uncertainties and therefore are the largest contributor to uncertainties in the proton stopping power. Notably, RLSP is proportional to the relative electron density, ?????
 ρ e r e l
 with the factor of K , which is the ratio of the Bethe-Block formula between tissue and water. Although the Bethe-Block formula for stopping power depends on the proton beam energy, the ratio K is a very slow-varying function of energy and is almost independent of β for the range of proton energy relevant to proton therapy. In fact, the largest difference between 175-MeV and 100-MeV proton beams is about 0.2% for cortical bone. For human tissues, the values of K are within 0.95 to 1.03. The difference in K is caused by the different mean ionization potentials of tissue and water; the effect is reduced because of the logarithm dependence of the mean ionization potential.
5.

Create the final calibration curve with appropriate fit through the data points (stopping powers vs. CT numbers). An example of a calibration curve is shown in Fig. 3.2 .

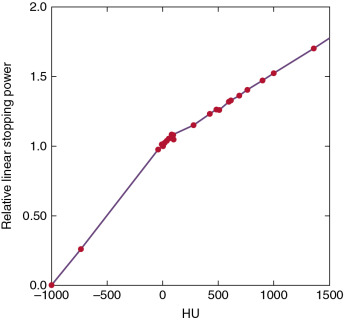
Fig. 3.2

Example of a computed tomography (CT) number (Hounsfield unit [ HU ]) versus relative linear stopping power calibration curve for a 120-kV CT scanner, derived by the stoichiometric method.

In step 1, measurement of the CT numbers of tissue substitute inserts should involve placing the inserts at the center of the phantom with two different sizes, with the smaller size representing the head and the other larger one representing the body ( Fig. 3.3 ). The average CT number of each tissue substitute insert from the head and body phantom should be used to reduce the beam-hardening effect. The CT-number-to-stopping-power curve established by the stoichiometric method reflects the ICRP reference values for human tissues. Because nonbiological materials used for immobilization devices (such as acrylic) may not fall on the calibration curve, ^, the proper CT number must be associated with the correct stopping power value assigned to the nonbiological material such that the water-equivalent thickness (WET) value is correct during the treatment planning process. (Examples of common nonhuman tissue materials encountered in proton therapy are listed in table 14.2 of reference .) It is also recommended to validate the CT number to RLSP calibration using a biological tissue sample.

Detectors and measurement techniques

Dosimetric quantities to be measured during commissioning are used to meet the following overall goals: (1) define the monitor units (MUs), dose-monitor linearity, and output calibration; (2) define the dose and spot position accuracy; (3) provide beam data for the TPS; (4) verify the TPS; and (5) establish the quality assurance program.

Ionization chambers

Both Farmer-type cylindrical and parallel plate chambers are used for measurements in passive scattering beam and pencil beam scanning (PBS) proton therapy. The general principle is that Farmer-type cylindrical chambers are used for measurements in uniform, low-dose gradient regions, and parallel plate chambers are used for measurements involving high-dose gradients (e.g., depth dose measurements). For the correction factor, P _ion, for the recombination losses of these ionization chambers in proton beams, one should carefully determine which published formula, such as ones by International Atomic Energy Agency (IAEA) TRS-398, are most appropriate for a particular beam condition. For example, Sahoo et al. found that for synchrotron-based PBS, the two-voltage formula for the continuous beam was the most appropriate. Also, for higher instant-dose-rate beams such as those in some cyclotron-based PBS systems, the normal bias voltage of 300 V may not be high enough to keep the P _ionlower than 1.01, and thus, a higher bias voltage, such as 400 V, may be necessary. The polarity correction factor and temperature and pressure correction factors should also be determined when using these ionization chambers.

Integral depth doses: Measurements and corrections

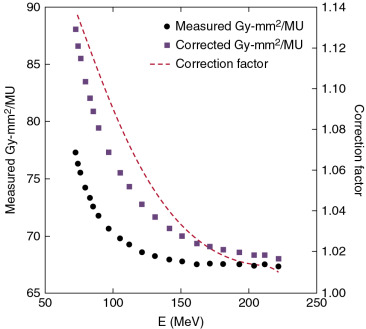
The data required for the TPS include the integral depth dose (IDD) for each energy and the in-air lateral dose profiles. The IDD is defined as the integral of dose for a single spot over a very large plane normal to the beam direction (i.e., the total dose deposited at a specific depth and has the unit of Gy-mm ² /MU), otherwise known as the Bragg curve. The detectors used for IDD measurements are large parallel-plate ionization chambers such as the PTW Bragg peak chamber (BPC) (model 34070, PTW-Freiburg, Germany), which has an effective radius of 4.08 cm and a nominal sensitive volume of 10.5 cm ³ . The effective measurement point for the BPC is at the inner surface of the front window, which has a WET value of 0.4 cm. Measuring the IDD with the BPC scanning in a three-dimensional water tank requires an electrometer with an extended dynamic range. The synchrotron pulse signal can be conveniently used to trigger the water tank scanning system.

A parallel plate chamber with radius ?≥3?????=3?2???+2(0.0307R)2‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾√
R ≥ 3 σ s p o t = 3 σ a i r 2 + 2 ( 0.0307 R ) 2
is recommended for accurate measurements of IDD, where σ _spotis the largest spot size for the beams to be measured, σ _airis the in-air spot size, and R is the range of the proton beam. The term 2(0.0307R) in the expression above represents the contribution of multi-Coulomb scattering within the patient to the beam size. The radius of the BPC may not be large enough to capture the entire low-dose envelope because of multiple Coulomb scattering and nuclear interactions, and so correction factors based on Monte Carlo (MC) simulations may be needed. ^, The correction factor can be defined as C(?,?;?1,?2)=?????(?,?;?2)?????(?,?;?1),
C ( E , d ; r 1 , r 2 ) = I D D M C ( E , d ; r 2 ) I D D M C ( E , d ; r 1 ) ,
where IDD _MCis the MC-calculated IDD at a depth of d , E is the energy of a pencil beam, r ₁is the radius of the BPC, and r ₂is the radius of virtual ionization chamber used by simulation and should be sufficiently large to ensure the accuracy of the IDD _MC. For example, an r ₂value of 20 cm was used for the PBS system at the University of Texas MD Anderson Cancer Center; the measured and corrected IDDs and correction factors at a depth of 2 cm as a function of energy for the MD Anderson pencil beams are shown in Fig. 3.4 . The correction factors ranged from 1.01 to 1.14 from the highest to the lowest energies. Notably, these correction factors would be different if the measurements were done at different depths. For the pencil beam with energy of 221.8 MeV at MD Anderson, for example, the BPC could underestimate the IDD by as much as 7.8% at a depth of about 18 cm. The measured IDD is determined by IDD _meas( E, d; r ₁ ) = M ( E, d; r ₁ ) N _D,WK _q ??21
π r 1 2
, where M ( E , d ; r ₁ ) is the corrected ionization chamber reading, N _D_, _Wk _qis the calibration factor multiplied by the beam quality factor, and ??21
π r 1 2
is the sensitive area of the BPC. Notably, no traceable national calibration standard has been established for the BPC chamber. Rather, users must determine N _D_, _Wk _qthrough cross-calibration with an ionization chamber calibrated by the Accredited Dosimetry Calibration Laboratory in a field with a uniform dose distribution. The dose uniformity within the sensitive volume of the BPC would affect the accuracy of N _D_, _Wk _qvalue. A preliminary report of a difference in the values of N _D_, _Wk _qdetermined for cyclotron and synchrotron beams suggested a possible dose rate dependence. This observation should be further investigated.