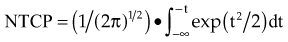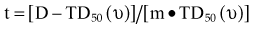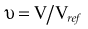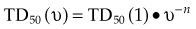Conformal Therapy Definitions

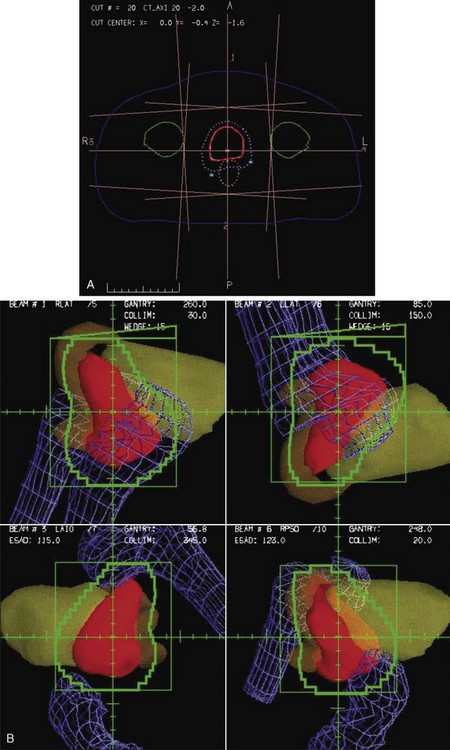
Conformal therapy describes radiotherapy treatment that creates a high-dose volume that is shaped to closely “conform” to the desired target volumes while minimizing (as much as possible) the dose to critical normal tissues. A more recent enhancement of the definition of conformal therapy incorporates the fact that the conformal plan is designed to conform to all the target dose requirements (shape; a possibly complex, desired dose distribution inside the target) while minimizing the normal tissue doses. Although these features are the general aim of any radiotherapy treatment, normally the term conformal is applied to treatment plans in which (1) the target volumes are defined in three dimensions using contours drawn on many slices from a computed tomography (CT) (or other) imaging study, (2) multiple beam directions are used to cross fire on the targets, (3) the individual beams are shaped or intensity modulated to create a dose distribution that conforms (in shape and dose) to the target volume shape(s) and desired dose levels, and (4) appropriate use is made of image guidance, accurate patient setup and immobilization, and management of motion and other changes to ensure accurate delivery of the planned dose distributions to the patient, so that deviations from the planned treatment of the patient are minimized. Figure 15-1 illustrates the conceptual difference between standard and conformal therapy: Figure 15-1A shows a standard four-field box treatment for a given target volume that everyone would agree is a nonconformal approach, whereas Figure 15-1B shows a conformal approach achieved with conformally shaped fields.

Figure 15-1 A, Four-field box treatment of the prostate. Contours shown include blue external contour, red prostate, dotted PTV, yellow (dotted) rectum, and green femoral heads. B, Beam’s-eye view of a nonaxial four-field conformal plan for prostate treatment, where the green outlines show the conformally shaped MLC patterns for each field. Red is prostate, blue is femoral heads, yellow is bladder, and brown is rectum.

A number of different treatment planning techniques and various treatment delivery techniques are routinely used to perform clinical conformal therapy. Three-dimensional conformal radiotherapy (3DCRT) was the first conformal therapy technique developed, based on use of 3D treatment planning and multiple cross-firing, carefully shaped fixed fields. A newer technique, inverse planning, involves creation of the radiotherapy plan using mathematical optimization techniques; intensity-modulated beams are used (beams with a complex intensity distribution, rather than the flat fields described above). The combination of inverse planning and intensity-modulated beams is called intensity-modulated radiation therapy (IMRT). More recently still, the use of integrated megavoltage and/or kilovoltage diagnostic imaging with modern treatment accelerators has led to image-guided radiation therapy (IGRT), which typically implies the integration of image-based patient positioning or monitoring with modern IMRT or 3DCRT. Active consideration of patient and respiratory motion in the planning or treatment of the patient is described by four-dimensional (4D) imaging and 4D planning.

In general, there can be many different combinations of technologies used to develop and implement sophisticated conformal therapy. Conformal therapy is defined by the kinds of dose distributions that are created for treatment of the patient, not by the specific techniques that are used. In other words, one often performs conformal therapy by using IMRT, but the fact that IMRT is used does not necessarily imply that the treatment is conformal.

A Short History Of Conformal Therapy

For many decades it has been known that delivering a high dose to the tumor is critical for control of the tumor and that the probability of complications increases with radiation dose and volume of organ irradiated. The basic concept of conformal therapy was elucidated quite early: One wants to treat the tumor to a high dose while minimizing the dose to normal tissues. However, it was not until the 1950s and 1960s that techniques recognizable as modern conformal therapy began to be developed.

One of the most important pioneers in “conformation therapy” was Shinji Takahashi, who described many of the important concepts of conformal therapy delivery and 3D treatment planning in a 1965 monograph.¹ Takahashi’s innovations included early multileaf collimators, automated (mechanical) conformal beam shaping, dynamic conformal treatments, orthogonal light beams to identify the machine isocenter, and 3D tumor models based on early tomography.¹ Other notable work in this area was performed by Harold Perry and colleagues² in Detroit and by Proimos, Wright, and Trump at the Massachusetts Institute of Technology (MIT)–Lahey Clinic.^3–7 Another early approach to conformal therapy, known as the Tracking Cobalt Project,^8,9 was led by Green, Jennings, and others at the Royal Northern and Royal Free Hospitals in England. First reported in the late 1950s,¹⁰ and summarized by Jennings,⁸ a series of mechanical, electronic, and, finally, computer-controlled treatment machines were developed to track disease spread, particularly along lymph node chains. By 1980, the computer-controlled version of the tracking system was in clinical use,¹¹ although Brace summarized the major limitations to the delivery technique: “The major obstacle to the routine use of conformation therapy is treatment planning.”¹¹ Finally, workers at the Joint Center for Radiation Therapy (JCRT) in Boston added computer control to a modern linear accelerator, so that the treatment table, gantry, collimator, collimator jaws, dose rate, and other parameters could be controlled dynamically while the beam was in use. The JCRT achieved the delivery of what is now called “dynamic conformal therapy,”^12–1415 a modern basis for computer-controlled conformal therapy.

As already described in the quote (above) by Brace, treatment planning was one of the main limitations for the conformal delivery techniques that were developed during this time period. The introduction of computed tomography (CT) in the early 1970s was a key to the development of the modern 3D planning that is crucial to conformal therapy, because it made available a complete 3D description of the anatomy of each patient that could be the basis for planning. Early evaluation of the use of CT in treatment^16–18 quickly led to widespread use of CT-based planning (see Ling¹⁹) as well as new interest in the use of inhomogeneity-corrected dose calculations, because CT provided the necessary electron-density maps of the patient.²⁰ Other imaging data, including magnetic resonance imaging (MRI) and positron emission tomography (PET), also became available and began to be used for planning in the mid-1980s.²¹

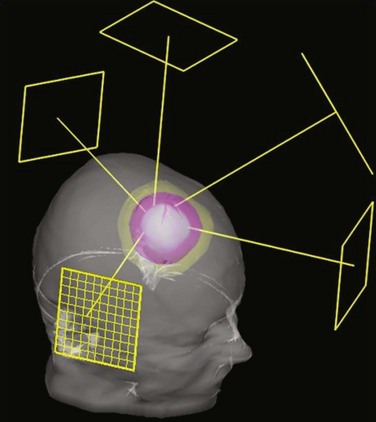
With the widespread implementation of CT-based planning, it became possible to make use of continuing improvements in computer technology and new software developments to create fully 3D treatment planning systems that incorporated 3D graphics and the “beam’s-eye view” (BEV), a 3D graphic reconstruction of the patient anatomy projected into the divergent geometry used by the x-rays in the radiation beam^22–26 (Fig. 15-2). Using BEV displays to design field shaping²⁷ and evaluate coverage of tumor and sparing of normal tissues is perhaps one of the most effective concepts in the entire 3D planning paradigm. Routine clinical use of 3D radiation treatment planning (RTP) began in 1986,²⁸ and many academic centers began development and then use of 3D planning systems in their clinics.^29–32

Figure 15-2 Beam’s-eye view of a brain tumor showing a multileaf collimator shaped to the violet target volume. Normal tissues include brainstem (white), chiasm (green), and optic nerves (red).

The development of 3D treatment planning systems helped drive the need for and design of more sophisticated treatment delivery systems because the 3D planning systems demonstrated treatment improvements that would be possible to use clinically if more sophisticated machinery were available to make efficient delivery possible. The first treatment machine designed specifically to perform computer-controlled conformal radiotherapy (CCRT), the Scanditronix MM50 Racetrack Microtron, was developed during this same time period.^33,34,35 Among other unique features, this machine included a fully computerized control system and a computer-controlled multileaf collimator (MLC)³⁶ consisting of two sets of thin tungsten leaves that are used to shape the radiation field. Virtually all other radiation therapy machines have since that time also implemented computer control systems and MLC systems.^37–39

The capabilities of computer control and MLC systems have made possible the delivery of very complicated plans, including those that make use of modulated intensities (a beam with different intensities in different parts of the field). Intensity modulation created using multiple segments^{40–43,44,45} or dynamic MLC motions^33,46,47 and computer plan optimization (inverse planning)^{48,49–51,52} have been integrated into IMRT.⁵³ The basic concepts of IMRT were described in 1987 by Brahme^33,48,54 and a practical implementation was described by Bortfeld soon after.⁵⁵ The combination of the flexibility of computer-controlled IMRT delivery with sophisticated plan optimization techniques has made IMRT an extremely powerful tool that can be used to perform conformal therapy.

The initial commercial IMRT implementation by NOMOS in 1992⁵⁶ was a form of IMRT now called serial tomotherapy, in which patients were treated slice by slice (as with early CT scanners) by the machine rotating around the patient and a special multileaf collimator (MIMIC) that performed the intensity modulation. Within a few years, all major vendors had implemented MLC systems with leaf widths varying from 1 cm to a few millimeters that could perform IMRT using either dynamic motions of the MLC leaves (DMLC) or a number of static segments (shapes), now called SMLC.⁵³ A more sophisticated implementation of tomotherapy based on helical delivery of IMRT, helical tomotherapy,⁵⁷ also became widely disseminated. In the last several years, a number of vendors have now developed a rotational MLC-based IMRT technique (IMAT), which was originally described by Yu,⁵⁸ and is now called VMAT (volumetric modulated arc therapy).^59,60 Inverse planning has also developed substantially during this time. Though much of this optimization makes use of quadratic weighted sum cost functions and simple gradient-based search algorithms, there have also been developments of sophisticated cost functions⁶¹ and the use of more biologically related costs such as normal tissue control probability (NTCP) models and equivalent uniform dose (EUD). Most systems use the weighted sum cost functions, but there has been development of sophisticated multicriteria methods^62,63 that more directly take into account the numerous optimization goals involved in a typical clinical radiotherapy treatment plan.

One of the developments that made the conformal therapy revolution possible was the development of amorphous silicon flat panel imagers,⁶⁴ which allowed effective electronic portal imaging verification of the accuracy of these newly conformal fields. This technology then was further developed, first for kilovoltage (diagnostic quality) imaging and then to provide cone beam CT (CBCT) capability using kilovoltage imaging systems mounted directly on the treatment machine.⁶⁵ The availability of these high-quality CBCT or kilovoltage imaging modalities directly on the treatment machine led to the development of image-guided radiation therapy (IGRT), in which diagnostic imaging was used to correct patient setup and positioning for treatment every day. IGRT processes have greatly increased the delivery accuracy possible and have led to the possibility of much smaller margins for setup errors, as well as enough confidence in targeting accuracy that stereotactic body radiation therapy (SBRT) is now used routinely to give very high doses (as high as 20 Gy/fraction) to well-localized targets in the liver, lung, and other sites. The use of IMRT and the proper handling of patient motion, respiration, and other “4D” issues is a major thread of much research and development at the current time.

Issues For Clinical Use

A number of important clinical features are crucial for planning and delivery of high-quality conformal therapy, and these issues should be carefully considered throughout the conformal therapy planning and delivery process.

Planning For Conformal Therapy

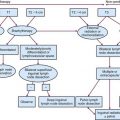
Treatment planning is one of the most critical parts of the conformal therapy process. In this description, we include all preparatory aspects of the planning process, including many activities that occur outside the radiation therapy planning (RTP) system. Many treatment delivery issues (e.g., setup accuracy, patient motion, portal and localization imaging) are briefly mentioned here and are more completely described later. Figure 15-3 shows a schematic of the basic components of the planning process for both forward (interactive) and inverse planning (i.e., IMRT optimization).

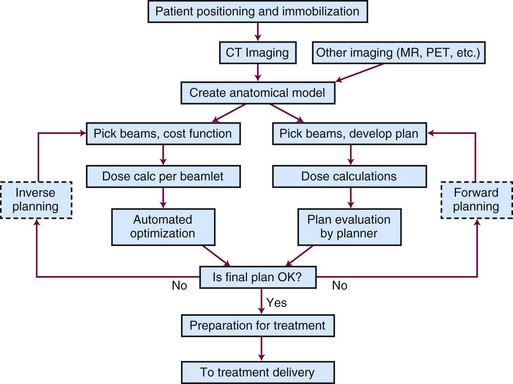
Figure 15-3 Schematic chart of the basic components of the planning process—shown for both forward and inverse planning.

Anatomy for Treatment Planning

Treatment planning is a computer simulation of the process of radiotherapy treatment, and it is based on creating a model of the patient inside the planning software, simulating radiation beams and the dose that those beams deliver to the patient. The definition of the virtual model of the patient, based on CT, MRI, and other types of imaging data, and how that anatomic model is used are crucial parts of the radiotherapy treatment planning process.

Three-Dimensional Anatomic Model

To allow conformal therapy planning, the representation of the patient that is used for treatment planning must be realistic and three-dimensional. In general, the basic data used to define the anatomy come from a CT study, typically consisting of 50 to 200 CT scan slices. The anatomic model of the patient is based on this CT data and consists of a number of objects (structures) that delineate organs or other objects (e.g., target volumes) in 3D (or 4D; see Motion, Setup, and Four-Dimensional Anatomy). These structures can be defined by (1) a series of contours, (2) a 3D surface description, (3) a voxel-based description, or (4) a set of points distributed either randomly or on a grid. Methods used to delineate these structures are described in the section on Structure Delineation and Contouring.

The 3D anatomic structures are crucial to the planning process. The various target and normal tissue structures describe the areas to be irradiated or to be spared (respectively) so that beams can be oriented and shaped. Graphic display of the 3D structures can also be used for geometric registration of the treatment planning anatomy to localize images obtained during simulation or treatment procedures. The external surface (and any inhomogeneities) are used for the dose calculation process. Most plan evaluation tools (e.g., dose-volume histograms [DVHs]) make use of these 3D structures for plan evaluation of the planned dose distribution.

Structure Delineation and Contouring

One of the most important and time-consuming aspects of the entire conformal therapy process is the delineation of the 3D anatomic objects (structures) used for planning and plan evaluation. It would be nice if all the anatomic structures could be automatically delineated once the CT data (and other imaging data) were obtained, but in general, this technology does not yet exist. Most anatomic structures are delineated by drawing contours on top of each of the CT (or other) images that are available. Because several hundred CT slices are often used, and there are many organs of interest that appear on each CT slice, there are many contours to be defined. Clever computer graphics drawing tools and techniques can make this easier, but defining the contours still requires much effort and care.

Accurately defining the structure contours is a critically important aspect of the conformal therapy process; because it defines the target and normal structure extents for the entire process, any error or inaccuracy becomes a systematic error throughout the entire conformal process. Errors in the process may come from sloppiness, from not knowing what is being visualized on the image on which contours are drawn, from limitations in the accuracy of the scan information (e.g., motion during the scan acquisition), and from many other problems. It is important that the 3D character of the objects being outlined is handled correctly: for example, sharp corners or spikes in a contour on just one slice are usually incorrect, because such a structure will usually show related features on a number of images. To avoid this type of drawing problem, it is important to review all the contours serially or to visualize the 3D shape of the object, so that any unphysical “spikes” can be identified and edited.

Target Volume Definition and Margins

To plan and deliver conformal therapy, it is essential to accurately define the volumes that must receive high radiation doses, the “target volumes.” As described in detail in the International Commission on Radiological Units (ICRU) report ICRU-50,⁷² three kinds of target volumes are typically defined, as summarized in Table 15-1.

TABLE 15-1 ICRU-50 Target Volume Definitions

Abbreviation	Name	Description
GTV	Gross tumor volume	Volume of macroscopic tumor that is visualized on imaging studies
CTV	Clinical target volume	Volume that should be treated to a high dose, typically incorporating both the GTV and volumes that are assumed to be at risk due to microscopic spread of the disease
PTV	Planning target volume	Volume that should be treated in order to ensure that the CTV is always treated, including considerations of systematic and random daily setup errors and intertreatment and intratreatment motion

The gross target volume (GTV) is typically delineated by drawing the imaged tumor on each of the imaging studies that are available. CT is used often, but for many sites, MR and PET can be very useful. When multiple imaging studies are available, the GTV can be drawn on each study, and then, using dataset registration to geometrically align the different datasets (see Multiple Imaging Modalities: Dataset Registration and Fusion), one can transfer the different GTV contours onto a single dataset. How to combine the various GTVs defined is the subject of ongoing research; however, typically, one will combine or take the union of all the defined GTVs in order to make sure that no gross tumor is missed within the defined GTV.

The definition of the clinical target volume (CTV) is probably the most important thing that the physician does in the conformal therapy process, because the CTV defines the region that is supposed to be treated with the prescribed dose. The CTV typically combines the GTVs plus any volumes that may contain microscopic disease that has not been imaged. The CTV depends on knowledge of the patterns of disease spread and incorporates any other clinical knowledge of the disease or the specific risks for spread that apply to the individual patient. The CTV is usually created by combining two kinds of information: (1) often, an expansion of the GTV by some margin (0.5 to 1 cm, typically) is used to account for microscopic invasion, and (2) additional anatomic areas may be included in the CTV based on standard directions of spread for the particular tumor type. In the end, the goal is to outline all the areas that should receive the intended dose.

Whereas GTV and CTV definition are the job of the physician, definition of the planning target volume (PTV) is the responsibility of the physicist and treatment planner, as the goal of the PTV is to make sure that the CTV is adequately treated in the face of setup error, intertreatment and intratreatment motion, delineation errors, and other errors in the planning and delivery process. The definition of the PTV should be done with as much information as possible because the region between the CTV and PTV contours is all “normal tissue” and increasing the PTV margin will just cause more normal tissue to be irradiated.

Often, the PTV is designed by simply defining an isotropic margin (e.g., 1 cm), and the CTV is expanded by this margin to create the PTV (Fig. 15-4). This expansion should be performed in three dimensions because expansion of contours only in the axial plane will lead to PTVs that are not correct in the third dimension. If the uncertainties are not isotropic but are larger in one direction than in the others (e.g., due to respiration), then the margin to be applied should be anisotropic.

Figure 15-4 Noncoplanar IMRT plan for treating a brain tumor, with the ICRU-50 target volumes shown: gross tumor volume (white), clinical target volume (pink), and planning target volume (yellow).

There has been a great deal of work studying patient positioning, motion, and target volume delineation errors, and analysis of these issues has led to specific recommendations for the size of the margin (between the CTV and the PTV) that should be used for the PTV. As described in Consideration of Setup Error and Patient Motion, one reasonable method for deciding the PTV-CTV margin has been determined to be 2.5 × Σ + 0.7 × σ, where Σ is the standard deviation of the systematic error and σ is the standard deviation of the random errors for the population of patients treated in that particular site.⁷³ To apply this formula, it is important to have measured, for your institution and each clinical site, the two standard deviations. As can be seen from the formula, the systematic errors in the process, such as incorrect contouring or use of a nonrepresentative CT scan for target delineation, are much more important issues than random day-to-day setup errors.

Further discussion of other types of target volumes, including the internal target volume (ITV), is included later in the section on motion.

For an individual patient, there can be multiple sets of GTVs, CTVs, and PTVs because there is often a CTV and PTV that correspond to each individual GTV. In the head and neck, where often a number of different nodal CTVs need to be treated, it can be very important to develop an organized and clear naming convention for the various CTVs and PTVs.

Normal Tissues

Definition of normal tissues is also a critical task for conformal therapy because identifying the critical tissues will allow the treatment planner to avoid or at least minimize dose delivery to those normal tissues. The planning tools used to avoid these structures can be simple graphic tools such as the BEV display, which allows the planner to shape the radiation fields to avoid important structures, or it may involve detailed dosimetric and DVH analysis, as is often the case for IMRT planning.

In order to perform dose-volume histogram (DVH) or other dosimetric analysis, it is important that each organ to be analyzed be contoured completely because most current DVH data are characterized with respect to the whole organ’s volume (either absolute volume or as a percentage of the whole organ). This has several implications:

1 The CT scans or other studies for a given site must image all the relevant normal tissues completely as well as the tumor. For example, a lung tumor CT scan should always include images from the neck down to below the bottom of the diaphragm, so that the complete volume of the relevant normal tissues can be identified (e.g., lung, heart, esophagus, spinal cord).

2 Contouring of normal structures must be done consistently if the DVH information is to be useful. Whole organs should always be contoured. For tube-like structures (e.g., spinal cord, rectum, esophagus) that can often extend out of the region of the tumor, it is important to have a defined protocol for how the structure will be defined, so that the superior and inferior extents of the contours for the structure are specified (e.g., the rectum during prostate planning).

Multiple Imaging Modalities: Dataset Registration and Fusion

Although CT scans are the primary imaging modality used for radiotherapy planning, information from other types of imaging, particularly MRI and PET, can be very useful for identifying disease or better identifying functional or anatomic areas that should be spared. Target volumes and normal structures can be identified on these additional imaging datasets, and that information can be incorporated into the treatment plan along with the contours and data from the CT scans. As described before, a CT scan set is taken to be the geometric basis for the treatment planning because the CT data are of high resolution, are geometrically accurate, describe the electron density information needed for inhomogeneity corrections, and are quickly obtained.

Several issues need to be solved to make quantitative use of the additional imaging information.

• For each imaging procedure, the patient should be positioned within the imaging device using the same position and immobilization and localization devices as for treatment. However, there are often positioning differences that must be taken into account.

• Even if the patient positioning is perfect, the coordinate system used in the new imaging device is usually different than the coordinate system used by the original CT scan. Therefore a geometric registration of the new imaging information must be performed, to align the new images with the base imaging information. Otherwise, with different coordinates, one does not know how to map pixels in the new image dataset to the coordinates of the original image set.

• For many imaging modalities, for example, MRI, various kinds of distortion are possible. If the new image dataset has geometric distortions, then these must be corrected (or at least accounted for) before the imaging information can be transferred into the base coordinate system for use in planning.

• The resolution, slice thickness, and slice orientations of different imaging modalities can often be different than those of the original CT dataset, so any quantitative use of the new imaging data must also handle these kinds of differences.

To address these issues, the process of dataset (or image) registration is used to align the coordinates for the various imaging datasets so that information can be passed from one image set into a coordinate system to be used for treatment planning. The registration process finds the geometric transform between the new dataset’s coordinate system and the base coordinate system (typically, the CT scan). If one considers only rigid body registration, the transform can consist of x, y, and z translations, or both translations and rotations, and it can include scaling as well (although typically, the scale of each dataset is known accurately and should not be modified).

Handling of distorted image registration is an important current research topic. These efforts work to develop methods for mapping distortions from one system to another, so distortions due to imaging or to patient motion (e.g., respiration) can be taken into account. Many different mathematical methods have been employed, including thin plate splines, B-splines, demons, and others. However, the main current issue is that distortion is well handled for things that are imaged well, but there is no way to determine how to do the distortion mapping for tissues that are not well imaged. Most algorithms do not take into account anatomic constraints and sliding organs (e.g., the diaphragm and lungs during respiration). Much work remains here.

To determine the best registration transform, an optimization algorithm is applied to the problem. The optimization process consists of choosing the metric to be optimized (some metric that describes the quality of the registration) and choosing an optimization search algorithm that will perform the search over possible transforms so that the optimal one can be found. The metric can be something as simple as the sum of the squares of the distances between predicted and actual point locations, if it is possible to define point-based landmarks on both imaging studies, or it can be image-based metrics such as the correlation between gray scale values of two CT scans, or mutual information, that can be used to register different image studies (e.g., CT and MRI or PET). This is a rapidly developing area of research.

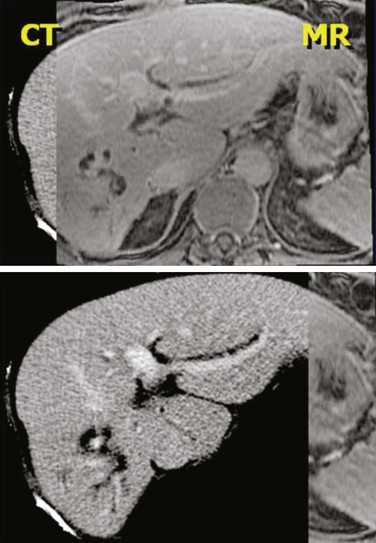
No matter what kind of registration algorithm is used, it is necessary to verify the registration and then to use the data from the various imaging studies. Verification typically consists of image-based or structure-based comparisons between the two datasets, with the goal of confirming that known structures from the two imaging studies accurately line up (Fig. 15-5). The quality of the registration depends on what parts of the images are most important clinically and must be reviewed by the planner/physician because at this point, no quantitative measure accurately takes into account all the clinical knowledge of the case. Once the registration is verified, then contours or 3D structure definitions from one dataset can be transferred into the base coordinate system for planning. This combination of data from multiple imaging sources is sometimes called image fusion.

Figure 15-5 Split-screen comparisons of CT (top) and MR (bottom) image data to confirm the accuracy of the geometric registration of CT and MR scans of the liver.

Motion, Setup, and Four-Dimensional Anatomy

So far, there has been little consideration of the facts that real patients breathe, move, are different from day to day, and change over time. Until recently, it was difficult to take such motions and localization differences into account within treatment planning, with the exception of defining appropriate PTV margins for the tumor. Fast helical CT scans, fast MRI, 4D-CT, and 4DCBCT imaging using the treatment machine have begun to provide detailed anatomic data as a function of time. These data have clearly demonstrated that a static anatomic description of the patient is not always appropriate and that treatment delivery schemes must also consider setup and motion effects if we are to achieve the optimal delivery of dose to the patient.

Several methods to handle motion and setup effects are in use or being investigated:

• As described in the section on Target Volume Definition and Margins, the standard way to handle motion and setup error is to determine the appropriate margin and then to expand the CTV by that margin to make a PTV that is the target for planning. If done correctly, the PTV ensures that the high-dose region always encompasses the CTV, even as the CTV moves around due to motion or setup error. The price, however, is that the larger the margin is, the more normal tissue is irradiated. Therefore, if the motion and setup error are taken more directly into account, this margin may be decreased, reducing the amount of normal tissue irradiated.

• One popular intermediate strategy for handling motion issues is to define the target volume extent at both ends of the respiration cycle. By combining those volumes, an internal target volume (ITV) is created that shows all the locations the target volume will move to during respiration, so it shows the envelope of volumes to be treated if the main goal is target coverage.

• Stereotactic treatments and treatments using daily setup correction (IGRT) try to significantly reduce the daily setup variations by carefully reproducing the position of the patient each day.

• With imaging with 4DCT, respiratory-correlated CBCT, and other such “4D” methods, it is now possible to visualize the motions of the tumor (and normal tissue) with the CT data, and to create structure outlines that better approximate the clinical targets and structures to be avoided. However, this technology is currently undergoing very rapid developments.

• With use of active breathing control (ABC), it is possible to control the breathing of the patient with the goal of turning on the treatment beam only when the patient is in the correct breathing state. This method can help minimize respiration motion and allow smaller PTV margins.

• It is also possible to gate the radiation beam, turning it on only when the target structure is in the correct location, based either on external markers or, potentially, on internal markers.

• Various radiographic and radiofrequency transponder markers are also used to help identify the position of the target. Transponders that identify their position 10 times per second allow real time tracking of the target and can help to dramatically reduce the PTV margin needed for treatment.

Over the next several years, a great deal of technical progress can be expected in this area.

Plan and Beam Definition

After the anatomic model of the patient has been established, the next major step in the planning process is to use the planning system to create a set of beams to be used for planning. This collection of beams, usually known as a “plan,” can be created using standard protocols (“treat all prostates with a four-field box of conformal fields”) or designed based on the specific anatomy of the case. Basic decisions on beam technique are typically made very early in the planning process, using experience and/or site-specific protocols. Typically, these decisions include picking the energy and number of beams, the basic orientations for the beams, and the type of beam shaping or intensity modulation to be used.

Beam Technique (Energy, Direction, and Type)

The first things to be decided as a treatment plan is generated are the number of beams to be used, their energy (and modality), and their direction. These choices are all interrelated, so typically this decision is based on standard experience or protocols. Although it is hard to summarize all of the useful ways to make this decision, there are a few standard rules that apply to most conformal planning.

• Avoid opposed beams. Simple nonconformal planning often used opposed beams (AP-PA and opposed laterals or obliques) to create a relatively uniform region of high dosage extending through the patient. For conformal planning, one typically wants to avoid pairs of opposed beams, because one wants to conform the dose to the target. For IMRT plans, this is even more important because opposed beams can cause degenerate solutions for the optimization search, leading to the optimization bouncing between two fairly equivalent solutions for opposing beamlets.

• Typically, lower energies are used for relatively superficial targets or for beams that traverse less normal tissue on the way to the target, whereas beams that must penetrate a greater volume of tissue are typically of higher energy. Changing energies for individual beams often makes a relatively small difference in the dose distribution achieved, and this possible improvement should be balanced against the additional complexity of the plan if multiple photon energies are used.

• For sites in which one is attempting to make sure the dose in the buildup region is relatively high, lower energies are usually used because there is less skin sparing for these beams.

• The most conformal plans can be achieved by ensuring that there are beams arranged around the target in all three dimensions, so that the plan includes some nonaxial beams.

• There is a great deal of debate (still) over the best energy beams to use for plans that involve large inhomogeneities such as the lung.

• As one creates more complex IMRT plans that have many degrees of freedom available to be optimized, it is possible to achieve very conformal plans. Typically, these plans include an odd number of fields, although the goal is just to make sure there are no opposing fields. There has been much discussion saying that IMRT plans can all be accomplished with 6-MV photons and that higher energies are not necessary, but there is little hard evidence to demonstrate that such a conclusion is correct. In addition, it is often said that IMRT plans can be achieved with only axial beams, but the use of noncoplanar beam arrangements will still result in at least slightly better plans (typically reducing somewhat the normal tissue dose for the same target conformality).

Shaping with Blocks and Multileaf Collimator

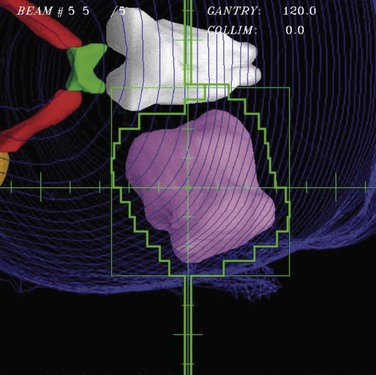
Although beam directions are important, shaping the radiation field to conform to the shape of the target volume is one of the crucial and defining concepts for “conformal therapy.” The shaping can be accomplished equally well by focused blocks or with an MLC, as illustrated in Figure 15-6. The conformal shaping of focused blocks is in fact “more conformal” than the jagged shape created by an MLC, although the MLC has a number of other advantages that have led to its popularity.

Figure 15-6 Shaped blocks and multileaf collimators can be used to shape the beam conformally.

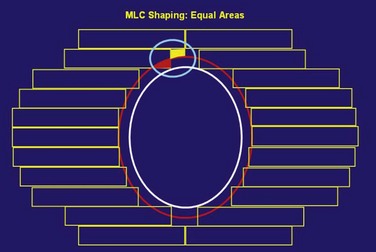
The routine use of conformally shaped fields designed during treatment planning depends in large part on the availability of the BEV display in the planning system because this view of the target shows the projection of the shape of the targets from the point of view of the radiation beam, which is what is needed to design field shaping. The simplest method used to conformally shape the fields (with either blocks or MLC) is to create a uniform geometric margin around the projection of the targets in the BEV and to set the shape to that margin, as shown in Figure 15-7. This method, the basis of the simplest type of conformal therapy, is sometimes called geometric conformation, or beam’s-eye view, targeting. Shaping a block to a given contour is easy, but with an MLC it is more complicated³⁸: The most commonly used method is the so-called equal area method (Fig. 15-7).

Figure 15-7 When using geometric conformal shaping for an MLC, the most common method is to create a contour at the desired margin (red contour) and then push the MLC leaves up to that contour so the areas overlapped and underlapped by each leaf are equal.

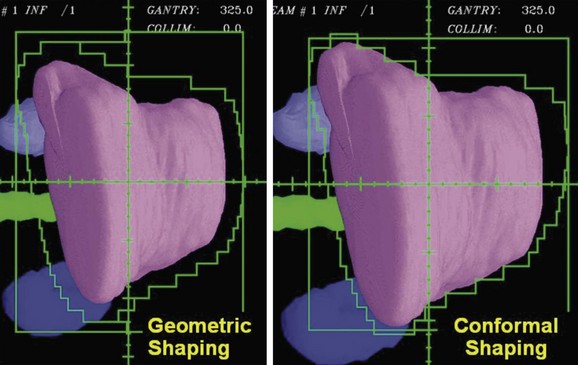
Using a uniform geometric margin for the field shaping does not lead to the most conformal dose distribution. To truly conform the dose distribution to the target, one must optimize the shaping of each of the beams so that the dose distribution is conformal. Figure 15-8 demonstrates the types of differences that occur when beam shapes are designed with a uniform margin and when the shapes are optimized to conform the dose to the target. Beam directions, the penumbra, and how the beams cross fire on the target affect the margins required for individual beam shapes.

Figure 15-8 Beam’s-eye view of conformal fields: uniform geometric margin (left) and conformal dose distribution (right). Using a uniform geometric margin typically does not achieve a dose distribution that is as conformal as possible. For this three-field pancreas treatment plan, the beam on the right had its shape optimized to make the dose distribution more conformal to the target.

Collimator angle is one more thing that can directly affect the conformality of a plan, mainly when an MLC is used. The leaves from an MLC move in only one direction, so to minimize the “stair-step” or jagged edges caused by MLC leaves when shaped to an angled contour, one may use collimator rotation to cause the MLC leaves to best fit the shape of the target or normal tissue. By minimizing the jaggedness of the MLC edges, one can decrease the amount of penumbra in that particular region of the beam, thereby allowing the beam to do a better job making a sharp penumbra between a target and normal tissue. For example, for beams trying to make a sharp dose gradient between the prostate and the rectum, rotating the collimator to parallel the edge of the rectum can help make the edge sharper.

It is possible to create intensity-modulated beams using a limited number of MLC-shaped “segments” all from the same gantry angle. This “segmental” IMRT can be created using the normal interactive planning paradigm (“forward planning”)⁷⁴ or the limited number of segments can be created by an inverse planning paradigm (see, e.g., “direct aperture optimization”).⁷⁵ The use of a few segments to improve target homogeneity (e.g., in the treatment of breast cancer with tangential fields) is a logical extension of the concept of wedged tangents when 3D planning is available.

Other Beam Technique Decisions

There are numerous other decisions to be made when creating the plan.

• One must choose the intensity of each beam, typically called the beam weight. How this decision is made depends on the specific beam normalization methods used within the planning system. Because the beam weight or intensity is directly related to the number of monitor units (MUs) that will be delivered from each beam, it is essential that translation of beam weights into MUs be understood and carefully handled, because errors in this step deliver the wrong dose to the entire field.

• For certain beam combinations, use of wedges in the field can help achieve a more uniform dose in the target volume. Standard two-dimensional (2D) planning makes routine use of pairs of fields known as “wedged pairs,” where the wedges help compensate for the fields entering the patient at 90 degrees (or some other angle) to each other. For conformal planning in three dimensions, there is a broader range of combinations of fields for which wedges are useful. For example, a 3D cone has some number of fields placed around a cone, and each of the fields usually requires a wedge to keep the target dose uniformity. This beam distribution is the 3D analog of the wedged pair.

• When the target is near the surface of the patient, it is often difficult to achieve the desired dose coverage of the target due to low doses in the entrance region of megavoltage photon beams. In this case, some amount of bolus can be added to the skin of the patient, for one or more beams, so that the photon beams can transit more material, therefore decreasing the skin sparing. This bolus description can be designed using the planning system, as long as care is taken in creating the physical bolus so that it actually matches the description that was put into the planning system.

• Most conformal treatment plans are isocentric, with the isocenter of the machine placed within the center of the target, and the beams rotating around the isocenter in the target. Other arrangements are possible, depending on the geometry of the normal anatomy and targets. For some situations, it is also possible to create pseudo-isocentric beams, which use 3D table motions to move the patient away from the head of the machine along the beam central axis, so that the plan is apparently isocentric but with a larger source-to-isocenter distance than the machine has. This technique can be used to create a larger range of table and gantry angles that can be used for treatment without the machine’s head getting too close to the patient.⁷⁶

Intensity-Modulated Radiation Therapy

Soon after conformal therapy began to be used clinically in the late 1980s, Brahme,⁵⁴ Bortfeld,⁵⁵ and others introduced the idea of modulating the intensity across each radiation beam, assisted by computer-based optimization algorithms to help determine the intensities required of the different parts of the beam. IMRT is now commonly used to create highly conformal treatment plans.

Intensity-modulated fields can be achieved in a number of different ways. There is a continuum of situations ranging from a flat field to multiple shaped segments to a beamlet-type description created by either a series of SMLC segments or a dynamic DMLC sequence. For plan optimization strategies, there is a similar range from simple (forward) iterative planning to optimized (inverse) planning that is driven completely by a mathematical cost function. Typically, the most complex intensity distribution (IMRT) is generated with inverse planning, but it is also possible to perform optimization for flat field conformal therapy.⁷⁷

Beam design for IMRT depends on the type of planning to be used (forward or inverse) and the photon energies and beam arrangement expected and should consider the tradeoff between the planning goals chosen and the complexity of the plan that will be allowed. If simple multiple segments are planned, then the individual segments may be created by the planner, whereas for more complex IMRT planned with “beamlets,” the beamlet size (1 × 1 cm, 0.5 × 0.5 cm, etc.) to be used for planning will be chosen by the planner.

Dose Calculations

Once the initial treatment plan is designed, the next step is typically to perform a dose calculation, so that the planner and physician can evaluate the dose distribution expected from the plan. Currently, because biologic effects are not well documented and understood in general, the physical dose distribution is the main parameter that is used (1) to choose between plans, (2) to choose what dose to deliver to the patient, and (3) to evaluate the quality of various plans proposed by the planner.

Three-Dimensional Dose Calculations

Treatment planning dose calculations have been performed on one (or more) 2D slices (or contours) of the patient since the 1940s. Often, these calculations were performed by hand, from table or chart look-ups, using a single traced contour of the external shape of the patient on a single axial slice of the patient at the center of the treatment fields. Even if performed on a number of slices, these dose distributions were in principle 2D and did not give a complete description of the dose to be delivered to the patient.

Continuing increases in computer capabilities and improved treatment planning and dose calculation algorithm developments resulted in availability of 3D dose calculations in the 3D planning systems that became available in the late 1980s. Since that time, most planning systems have implemented 3D calculation algorithms that (1) calculate the dose throughout a 3D volume of points, (2) calculate the dose with algorithms that take 3D scatter into account, (3) have algorithms that take the 3D effects of inhomogeneities into account, (4) use a 3D description of the anatomy, (5) fully take into account 3D beam divergence, and so on. Because the calculation of dose with high resolution using an accurate and realistic dose calculation algorithm still takes a significant amount of time, every dose calculation algorithm and implementation makes tradeoff choices between accuracy, speed, computer resources needed, resolution, features and effects that are correctly modeled, and other factors. Determination of the appropriate mix of approximation, compromise, and robustness needed for particular kinds of clinical planning dose calculations is an important responsibility of the radiation oncology physicist.

To accurately perform planning for conformal therapy, accurate and 3D dose calculations must be performed. An accurate 3D anatomic model is required; the dose must be determined throughout the volume encompassing the targets and the critical normal tissues; and the calculations should be done at high resolution if one wants to know how conformal the plan actually is. It is critical that all limitations in the calculations be understood and the effects of those limitations should be considered in any clinical decisions that are based on the results of the calculations.

Algorithms

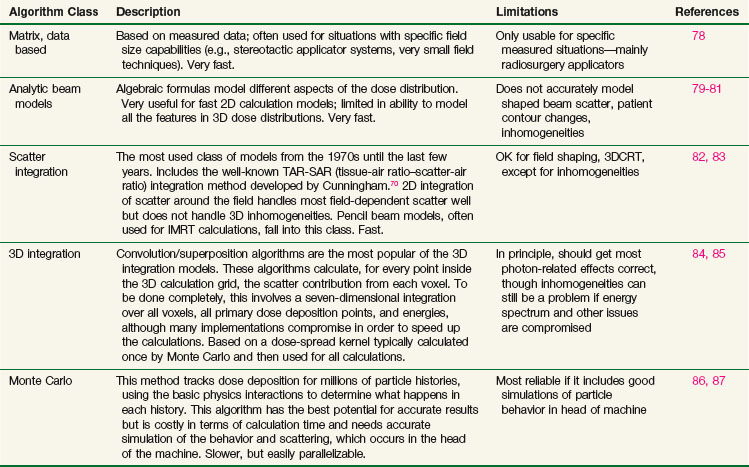
Many different types of calculation algorithms have been developed for photon and electron beams, and new improvements or implementations are continually becoming available. It is beyond the scope of this text to describe any algorithms in detail. Algorithms ranging from simple table look-ups based on measured data to Monte Carlo simulations that require many hours of central processing unit (CPU) time of the fastest computers all have their place and are the appropriate choice of algorithm for one particular situation or another. Table 15-2 summarizes some of the advantages and disadvantages of each class of photon algorithm. If there is a choice of algorithms for conformal planning, the choice should be made with careful consideration of the potential limitations of the chosen algorithm, and the radiation oncology physicist should carefully commission the algorithm for clinical use by comparison with appropriately measured data for the local machines in order to demonstrate the adequacy and limitations of the algorithm for clinical use.⁸⁸

TABLE 15-2 Advantages and Disadvantages of Each Class of Dose Calculation Algorithms for Photon Therapy

Other Dose Calculation Issues: Grids, Resolution, Inhomogeneities, and Other Issues

Aside from the inherent accuracy of the dose calculation algorithm that is used, many other user-controlled factors affect the final accuracy of the doses predicted by the calculations that are performed for a plan. Unfortunately, it is not possible to address all these issues with a few simple guidelines.

Every step of the treatment planning, dose calculation, and plan evaluation process involves decisions about how much time, effort, and precision to spend defining or reviewing each aspect of the planning, and the accuracy of the final product depends on all those individual decisions. If one chooses to calculate the dose on a grid of spacing of 0.5 × 0.5 × 0.5 cm, then it will be hard to evaluate the dose 2 mm from the target with a significant degree of confidence, given that dose gradients at the edge of a beam can be approximately 10% per millimeter. Highly conformal therapy will require that dose calculations be performed with high-resolution grids (perhaps, 2 to 3 mm), leading to very large numbers of points that need to be calculated and longer calculation times. Similarly, if truly conformal therapy is going to be performed in lung tumors, where inhomogeneities are significant, an advanced calculation algorithm that can accurately predict the dose in inhomogeneities should be used if one wants to understand the real dosimetric situation in the patient. For IMRT plans, there are further dose calculation-related issues (discussed later).

Plan Evaluation Tools

After the dose distribution from the plan has been calculated, the next step in the process is to evaluate the plan and the predicted dose distribution. Typically, the dose distribution is evaluated by looking at isotope curves on individual cuts through the plan, looking at isotope surfaces (3D displays of the isosurfaces), and then using DVH analysis of the dose delivered to individual organs. If the capability and appropriate data are available, it is also possible to use biologic modeling results such as normal tissue complication probability (NTCP), tumor control probability (TCP), and the equivalent uniform dose (EUD) to help with the plan evaluation.

Dose Display

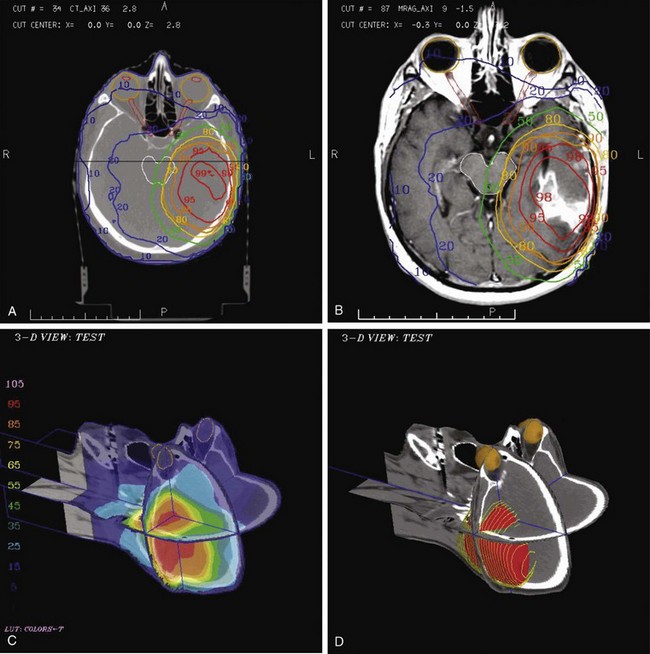
The most commonly used type of display of the dose distribution for a plan consists of displaying contour lines of constant dose, or “isodose lines,” on top of the anatomic information that was used for the plan. These kinds of displays have been used for many years—first with only the contours of the patient (obtained by hand measurement using solder wire or other techniques) and then later displaying the isodose lines on top of the CT scan. For conformal planning, not only axial cuts should be used for the isodose lines but also coronal and sagittal reformatted CT images, because display of isodose lines on multiple orthogonal cuts can give the planner a more 3D sense of the coverage of the target volume. 3D graphics techniques can be used to put the images and dose lines in 3D perspective, as shown in Figure 15-9. A variation of the isodose line display is the colorwash display, in which the dose level calculated for each pixel of the image is used to assign a color value (see Fig. 15-9C).

Figure 15-9 Dose display for a conformal brain plan. A, Axial CT with isodose lines. B, Axial MRI with isodose lines. C, Three-dimensional axonometric view with dose colorwash. D, Target volume (red contour) and isodose surface (yellow contour).

Any image that is part of the anatomic model of the patient should, in principle, be usable for dose calculation and dose display (though this is not always permitted by some TPS systems). If MRI, PET, or other image datasets have been registered with the basic anatomy, then the PET or MR images can also be the backdrops for the dose display. By comparing the location of the isodose lines with the contours of the targets and critical normal tissues, the planner and physician can evaluate the quality of the dose distribution that is obtained for this particular beam arrangement and decide whether the plan is adequate or whether further modification of the plan is necessary.

The goal of conformal therapy is typically to conform the shape of the high-dose region to the target in three dimensions, so display of the 3D dose distribution shape may be a help when evaluating the conformality of the plan. The 3D analog of an isodose line is called an isodose surface. Also, isodose surfaces, sometimes called “dose clouds,” are typically displayed in a 3D perspective graphic image (see Fig. 15-9D).

The dose displayed in isodose curves or surfaces, or any other dose display, can be shown in a number of ways. The most common mode used for conformal therapy is the relative dose distribution, where all the dose display is normalized to the dose value at the isocenter or center of the target. With this kind of relative dose normalization, typical conformal therapy plans would have the 95% isodose surface surrounding the target, with the shape of the 95% surface (or isodose lines) conforming to the target. One could, however, equally well display the dose in absolute terms so that the high-dose region demonstrated the desired total dose for the plan (e.g., 60 Gy) or the desired dose per fraction (e.g., 2 Gy/fraction). It is of course essential that the output of the plan that is used for treatment preparation should be carefully understood and documented, so that there is no confusion between the different ways the dose can be displayed.

Dose-Volume Histograms

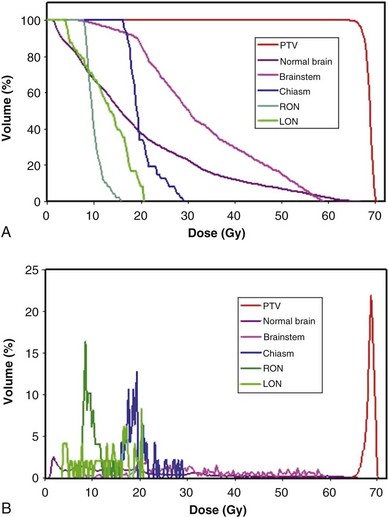
Review and evaluation of the dose throughout the patient in three dimensions can be complex and time-consuming processes, and it is also difficult to give specific guidelines for normal tissue or tumor responses with respect to that complex data. It has become standard to evaluate the dose received by the target volumes and normal tissues using DVHs. To form a DVH for any 3D object, one looks at the dose value for each voxel in the object and forms a histogram, counting the number of voxels that receive each different dose level. Because the volume of each voxel is known, the volume of the organ receiving each dose level is known. See the review by Kessler⁸⁹ for more detail.

Both the volume (vertical) and dose (horizontal) axes can be displayed in absolute terms (as cubic centimeters [cc] or Gray [Gy]) or in relative terms (% volume or % dose), depending on how the planner wants to analyze the results. DVHs are displayed in three different forms: direct, cumulative, and differential.

• The direct histogram is the generic form of any histogram, displaying the volume of the organ that receives dose within each dose bin (1% or 0.5 to 1 Gy is a typical dose bin width). The direct DVH is most useful for display of the dose-to-target volumes, because one can easily visualize the minimum dose, the maximum dose, and the dose most representative of the dose to the entire target volume (Fig. 15-10B).

• The DVH display most commonly used in radiotherapy is the cumulative DVH, in that the volumes receiving at least a given dose value are plotted. The cumulative DVH integrates the direct histogram, so it always begins at 100% (100% of the organ receives at least 0 dose), and ends at the maximum dose (see Fig. 15-10A). Figure 15-10A illustrates a desirable cumulative DVH for a target (PTV, which has a uniform target dose with no underdosing or overdosing of the target). Figure 15-10A also shows two normal tissue DVHs: normal brain, which has some volume of the organ receiving a high dose, and chiasm, with a smaller volume of organ receiving high dose, even though the mean dose of the two DVHs is about the same. Whether a normal tissue DVH shaped like the example normal brain DVH is better than one shaped like the example chiasm DVH is only known once reliable clinical data are obtained for the two situations.

• The third type of DVH used for radiotherapy analysis is the differential DVH. This type is necessary in order to appropriately compare DVHs formed with different dose bin sizes, because the volume contained in any dose bin changes as the dose bin size changes. The differential DVH plots (1/D_bin) _* DV/DD, so different differential DVHs can be compared even if their dose bin sizes are different.

Figure 15-10 DVH displays for a brain treatment plan. A, Cumulative DVHs. B, Direct DVHs. LON, left optic nerve; RON, right optic nerve.

DVH analysis is a very important part of conformal therapy planning, but DVHs of target and normal structures do not tell the entire story. The DVH of an organ summarizes the dose to that organ, but it does not give any information about the geometric distribution of the different doses within the organ. If the DVH for a PTV shows cold and hot spots, it is not possible to tell if either the hot spots or the cold spots are in the center of the PTV or along the edges. Whenever the location of some dosimetric feature may make a difference, it is important to review the dose distribution using dose display tools.

Minimum, Maximum, and Other Quantitative Metrics

DVHs are only one kind of dosimetric analysis that can be used for conformal planning, and many other kinds of analysis are possible. For example, simple dosimetric metrics are often used to help make planning decisions. The maximum dose allowed within a target volume, or inside critical organs, is often specified in conformal therapy protocols. Particularly for IMRT conformal plans, the maximum dose may be a fairly difficult metric to use clinically because it may depend strongly on the dose calculation grid spacing used and on details of the dose calculation algorithm implementation. A volume-based maximum dose criterion (e.g., the maximum dose to 1 cc of the object) is typically less sensitive to algorithmic details. Similarly, the minimum dose to the PTV is subject to the same algorithm-related limitations and may be of limited value, particularly for IMRT planning. Another common dose metric is the mean dose to a structure, often used to describe target doses and for certain volume-effect organs such as the lung and liver, where the normal tissue complication probability (NTCP) generally scales with the mean dose to the normal tissue.⁹⁰

Use of Equivalent Uniform Dose (EUD) and “Biologic Models”

To this point, all the treatment plan analysis has been based directly on the dose distribution. In reality, of course, it is the biologic effects that are important, especially the probability of controlling the tumor and of causing acute or late complications in normal tissues. Analyzing the dose distribution is in many ways a surrogate for the analysis that is really needed, the biologic effect analysis. It is expected that there will be major and continuing improvements in biologic effect knowledge and modeling over the coming years, and as these improvements happen, they should be integrated into use for treatment planning. At the moment, however, the only biologically related parameters that are commonly used in treatment planning are the NTCP, the TCP, and the EUD. This section discusses each briefly.

The most commonly used “biologically related” parameter used in treatment planning is the NTCP. The term NTCP actually has several meanings: (1) The NTCP is a probability that can be determined clinically for an organ; (2) there are NTCP models that attempt to model how the probability of a particular complication changes as a function of dose, volume of the organ irradiated, and potentially other factors; and (3) the NTCP is used as the value of the complication probability that has been determined by an NTCP model for a particular situation. It is important to make sure that it is clear how to differentiate between the real clinical NTCP, an NTCP model, or the particular expected value of the NTCP for a situation.

There are many kinds of models that have been developed for the NTCP, and these models have been applied to specific complications for many different organs. Discussion of these different models is beyond the scope of this work, and here we briefly describe only the most well known model, the Lyman NTCP model. John Lyman developed the three-parameter “Lyman” model early in the 1980s.^91,92 This power law model is a phenomenologic model that characterizes complications using three parameters: TD₅₀ for uniform irradiation, the slope of the dose sensitivity (n), and the volume parameter (m):

(Eq. 1)

where

(Eq. 2)

(Eq. 3)

(Eq. 4)

To use this model for a real clinical DVH, one typically uses the Kutcher-Burman DVH reduction method⁹³ to convert the clinical DVH curve into a DVH with a single dose and volume, which are then used inside Equation 1. Together, these techniques are typically called the LKB (Lyman-Kutcher-Burman) model.

When developing this model, Lyman made no claim that it was a real biologic model; he simply developed the simplest model that agreed with some of the most basic behavior of NTCPs, at least as characterized at that time. The model has been used extensively, either as a way to characterize complication data or for plan evaluation and comparison. A very important starting point for study of NTCPs of various organs was published by Emami,⁹⁴ who summarized a tabulation of then current knowledge of clinical complication expectations (based on a physician working group) using Lyman NTCP model parameters. Recently, complication data and parameterizations for many clinical sites have been reviewed by site-specific groups of experts in order to provide updated complication modeling information.⁹⁵ The Lyman model has proven to be a useful way to parameterize clinical NTCP data and has been used as part of dose escalation studies based on treating patients with a specific isocomplication level (for liver⁹⁶ and lung⁹⁷).

One of the most important things that can be done to improve conformal therapy planning is to perform clinical studies that (1) document, for each normal organ, the distribution of doses and volumes of various organs that are irradiated, (2) include careful patient follow-up, and (3) are analyzed to find the dose-volume-complication relationship for each organ. The dose-volume-complication relationship for each organ (and each complication) is unique and must be determined clinically. Once these results are known for all normal tissues, we will know better how to optimize treatment plans.

Just as the dose-volume-effect relationship is important to know for normal tissues, it is also very important to know for the tumor. The tumor control probability (TCP) is the subject of clinical studies and modeling and is a way of comparing expected tumor responses with planned dose distributions. A number of different models exist, including the Niemierko-Goitein⁹⁸ and Nahum⁹⁹ TCP models. Most of these models use various basic assumptions about tumor cell density and distribution, the statistical interactions between dose and tumor cell survival, and the incorporation of population-based statistics for tumor heterogeneity, and may also consider effects that depend on tumor stage, hypoxia, and other issues. Tumor cell biology and predicting local tumor control are very complicated subjects that are well beyond the abilities of current models. TCP modeling is used in a reasonably limited way because it is known that the predictions are of limited accuracy.

Only gold members can continue reading. Log In or Register to continue

Share this:

• Click to share on Twitter (Opens in new window)
• Click to share on Facebook (Opens in new window)

Related

Related posts:

Neutron Radiotherapy Hodgkin’s Lymphoma Penile Cancer Retinoblastoma Low-Grade Gliomas Cervical Cancer

Stay updated, free articles. Join our Telegram channel

Join