15.1
Introduction and background
The mineralized bones of the skeleton are critical to load bearing and locomotion of vertebrates. The structure of the tissue within the bones is well suited to the mechanical demands placed on the skeleton during physical activities. In the long bones the cortical diaphyses are essentially hollow tubes, an effective shape for the bending and torsional moments applied to the appendicular skeleton. The cancellous bone located in the ends of the long bones and within short bones such as the vertebra effectively transmits and distributes loads at the joints. While both cortical and cancellous bones have important metabolic roles, their forms are key to their structural function.
The loss of mechanical integrity of the skeleton results in fracture. Age-related fragility fractures primarily occur at corticocancellous sites such as the femoral neck and spine. Mechanically, fracture results from material and geometric changes that compromise the load-bearing capacity of the structure, leading to failure. Biomechanics has traditionally considered these structural changes in terms of conventional, mechanical, and material assessments, and a great deal has been learned about the age-related properties of bone tissue from these approaches. However, age-related changes in the skeleton can also be viewed as the end stage of a continuum of mechanical regulation of bone size and shape. Skeletal mass and architecture evolve in response to the mechanical stimuli experienced during the lifetime of the individual, producing a structure that is suited to bear functional loads. The aspects of bone material and geometry that contribute to fracture therefore reflect the history of biophysical stimuli integrated over the lifetime of the individual.
In this chapter, we view the skeleton from a mechanobiological perspective to understand the important role that loading plays in achieving peak bone mass during growth and preventing bone loss in the adult. A number of excellent reviews on the history of bone functional adaptation have been presented . Here, we review theoretical and computational investigations of functional adaptation of cortical and cancellous bone and discuss experimental investigations of the topic. We emphasize models of controlled in vivo loading to enhance bone mass that have contributed to recent advances. The effects of decreased loading and loss of bone with hormone deficiency are left to other chapters (see Chapter 32 : Estrogen deficiency and the pathogenesis of osteoporosis and Chapter 40 : Immobilization osteoporosis). Furthermore, the focus here is on preclinical models; clinical data are presented in later chapters.
15.1.1
Mechanobiology of bone mass during growth and development
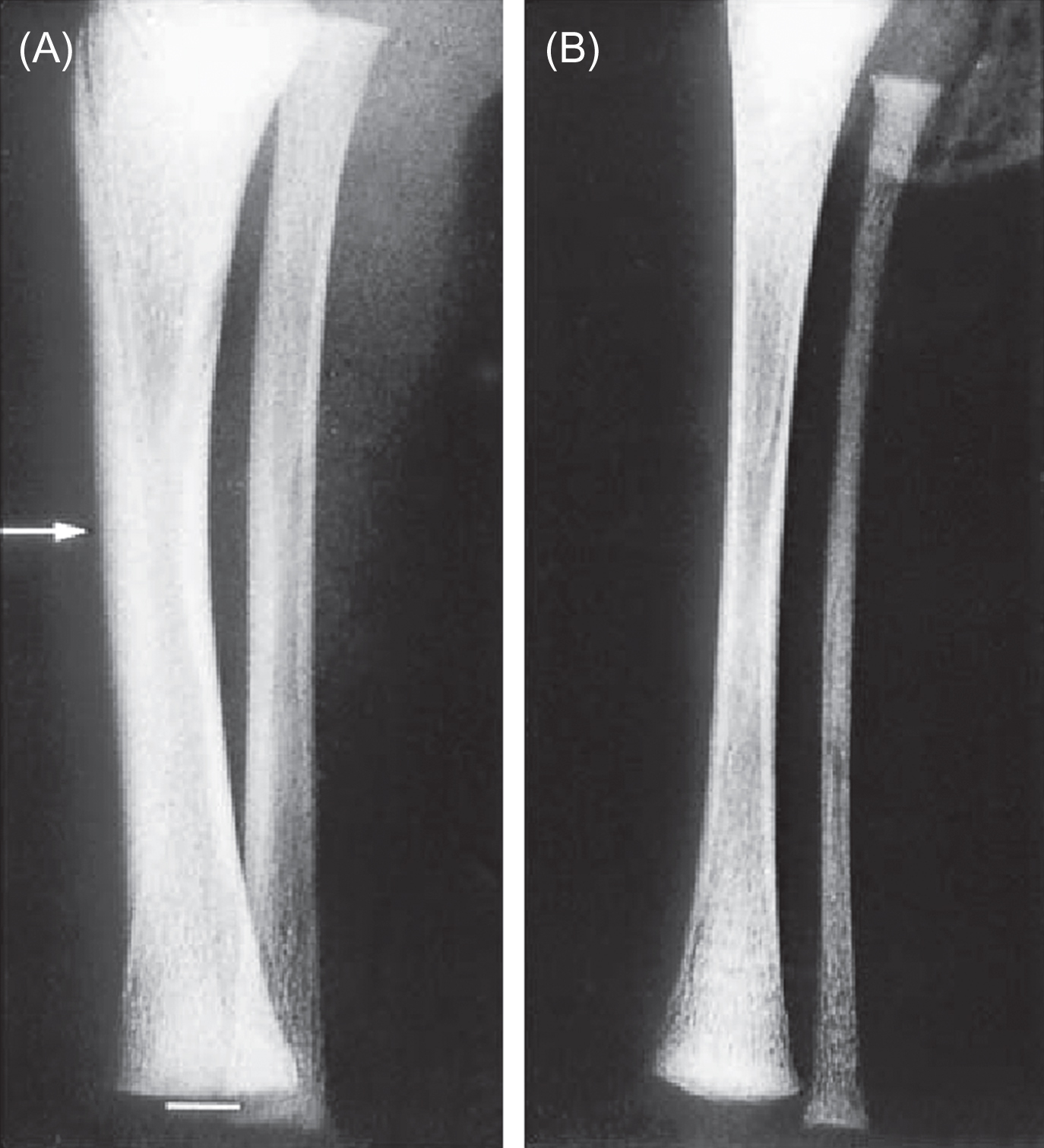
Many factors contribute to the development, maintenance, and subsequent degeneration of skeletal form, including genetics, hormones, and biophysical factors. The regulatory roles change with age and environment. Dynamic mechanical stimuli first become important regulators of skeletal structure during early skeletal development. The first prenatal muscle contractions are concurrent with the initiation of mineralization of the cartilaginous skeletal anlage. These forces contribute to the progression of the primary ossification front in the developing long bones. The absence of these in utero muscle forces inhibits the normal process of bone development, resulting in thin, fragile bones ( Fig. 15.1 ).
During growth and development, bone mass and strength increase with age until the adult form is reached. Postnatally, bone growth occurs by two mechanisms: continued endochondral ossification that increases bone length, and appositional bone formation that increases the diameter of the diaphysis ( Fig. 15.2 ). In addition to increasing bone length, cancellous tissue at the bone ends develops at the growth plate through endochondral ossification. Before skeletal maturity, body size and mass increase by an order of magnitude, increasing the loads due to body weight on the skeleton and driving appositional expansion of the periosteal and endosteal surfaces of the long bones. During this rapid growth period, bone tissue is metabolically active and the skeleton is highly responsive to loading .
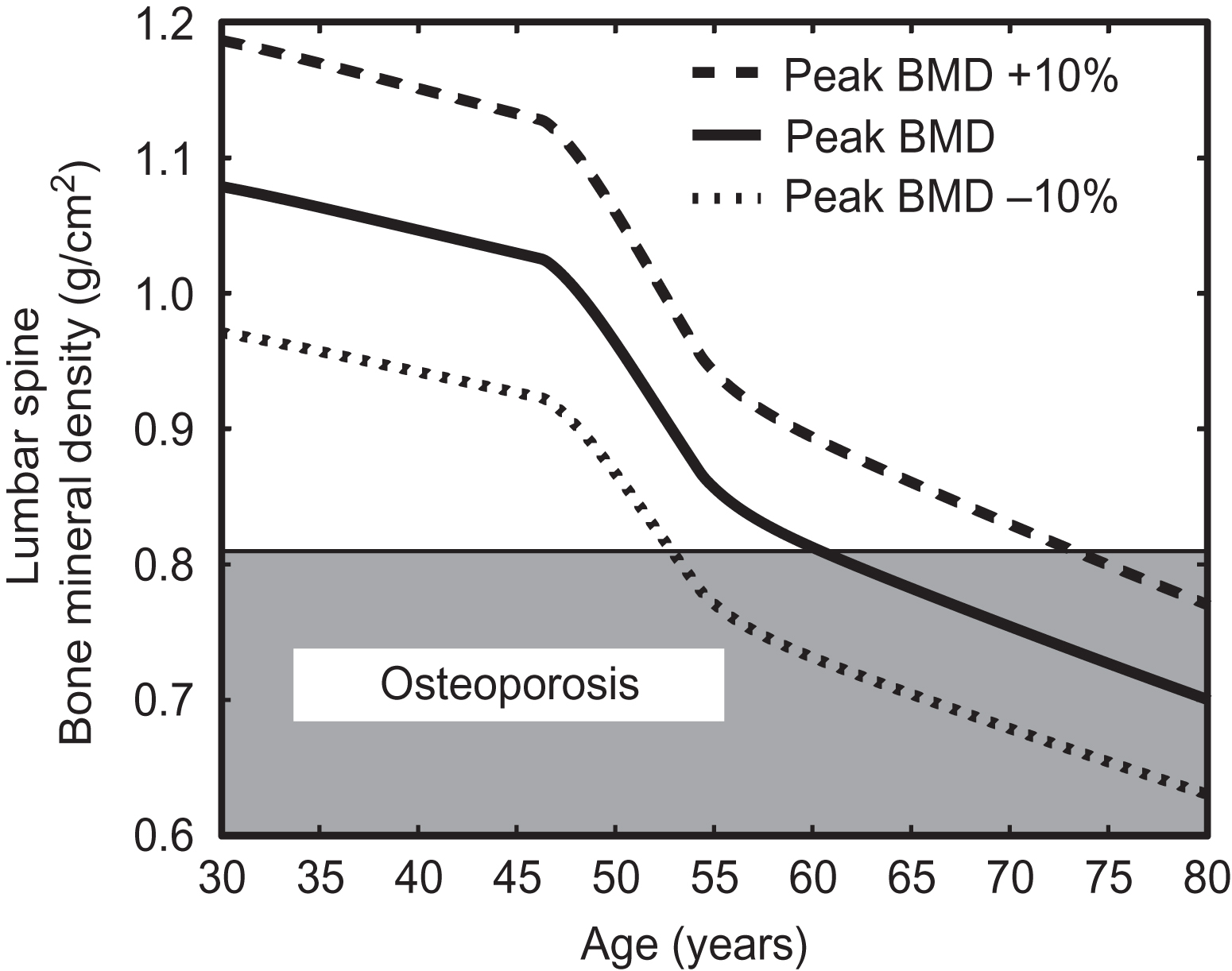
Following completion of growth in adulthood, the peak bone mass is achieved. The peak bone mass represents a critical maximum level of bone mass for an individual during his or her life. Failure to maximize bone mass during growth and development in early adulthood can contribute to the development of osteoporosis later in life. Comparison of different mechanisms of bone loss with aging suggests that an individual’s peak bone mass is a critical determinant of the onset of osteoporosis decades later, more so than other contributors such as the subsequent rates of bone loss ( Fig. 15.3 ).
After reaching peak bone mass, maintenance of the adult skeleton depends on the forces experienced during normal activity, but also reflects the prior developmental history. With aging and its accompanying hormonal and metabolic changes, mechanoresponsiveness often declines as do activity levels (see Section 15.4 ), diminishing skeletal mass and load-bearing capacity, which can result in fractures during normal function. Exercise to increase skeletal loading can counteract this bone loss (see also Chapter 22 : Physical activity, exercise, and skeletal health).
15.1.2
Simulating mechanical regulation of bone biology
The concept that bone tissue adapts to mechanical stimuli is often referred to as “Wolff’s Law” based on the writings of Julius Wolff, particularly his book “The Law of Bone Remodeling” . Based on the work of Culman, a Swiss engineer, Wolff concluded that the internal cancellous architecture of a bone followed mathematical rules. Wolff drew extensively on the work of Roux, a German embryologist, who proposed a mechanism of bone adaptation to mechanical loading. These ideas were further developed by D’Arcy Thompson in the early 1900s. These insightful descriptions and observations linking mechanics and bone growth planted the seeds for the field of bone mechanobiology. At the time, however, models of bone growth were purely descriptive as the ability to implement computational models of a bone structure subjected to mechanical forces was lacking. Modern advances in both computational power and imaging have allowed high fidelity computational models to be developed to simulate the mechanical regulation of bone development and adaptation. Computational and analytical models have facilitated our understanding of the role of mechanical stimuli in bone growth, maintenance, and degeneration. Here, we review theoretical and computational investigations of functional adaptation of bone and discuss the experimental investigations on the topic.
Conceptually, the regulation of bone mass by mechanical loads can be thought of as a simple feedback control system ( Fig. 15.4 ). Loads applied to the skeleton are the input to the system and drive changes in bone mass. The signals to change bone mass are registered by sensors and effected by actuators within the musculoskeletal system. Osteocytes are currently considered to be the primary mechanosensory cells (see also Chapter 7 : Osteocytes) , but other cells resident in the skeleton may contribute, including osteoblasts, lining cells, and undifferentiated precursor cells. The actuator of the system is responsible for changing bone mass and is currently the most well-understood component. In the healthy skeleton the actuators to add and remove bone are the bone-forming cells, osteoblasts, and bone-resorbing cells, osteoclasts.
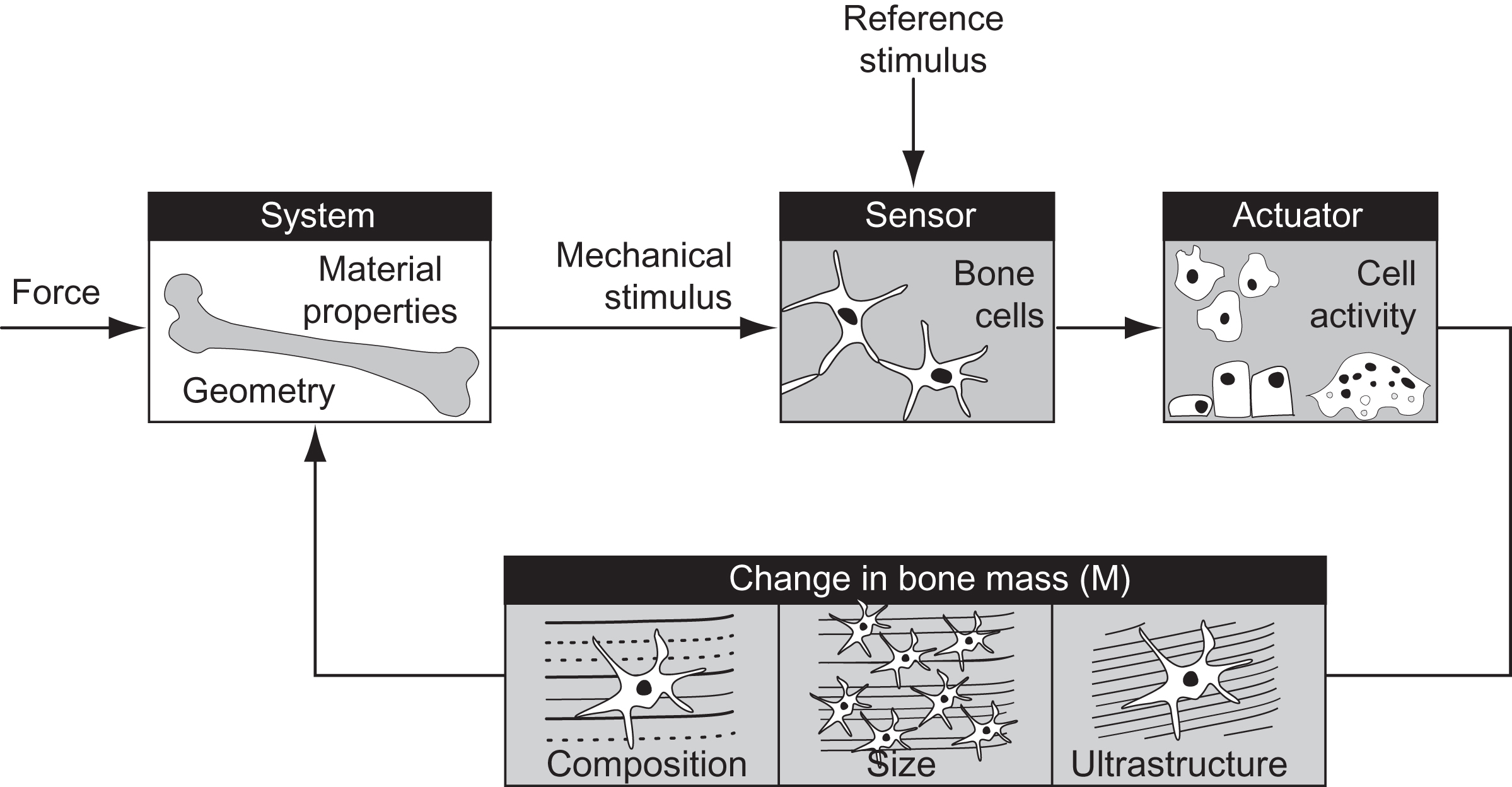
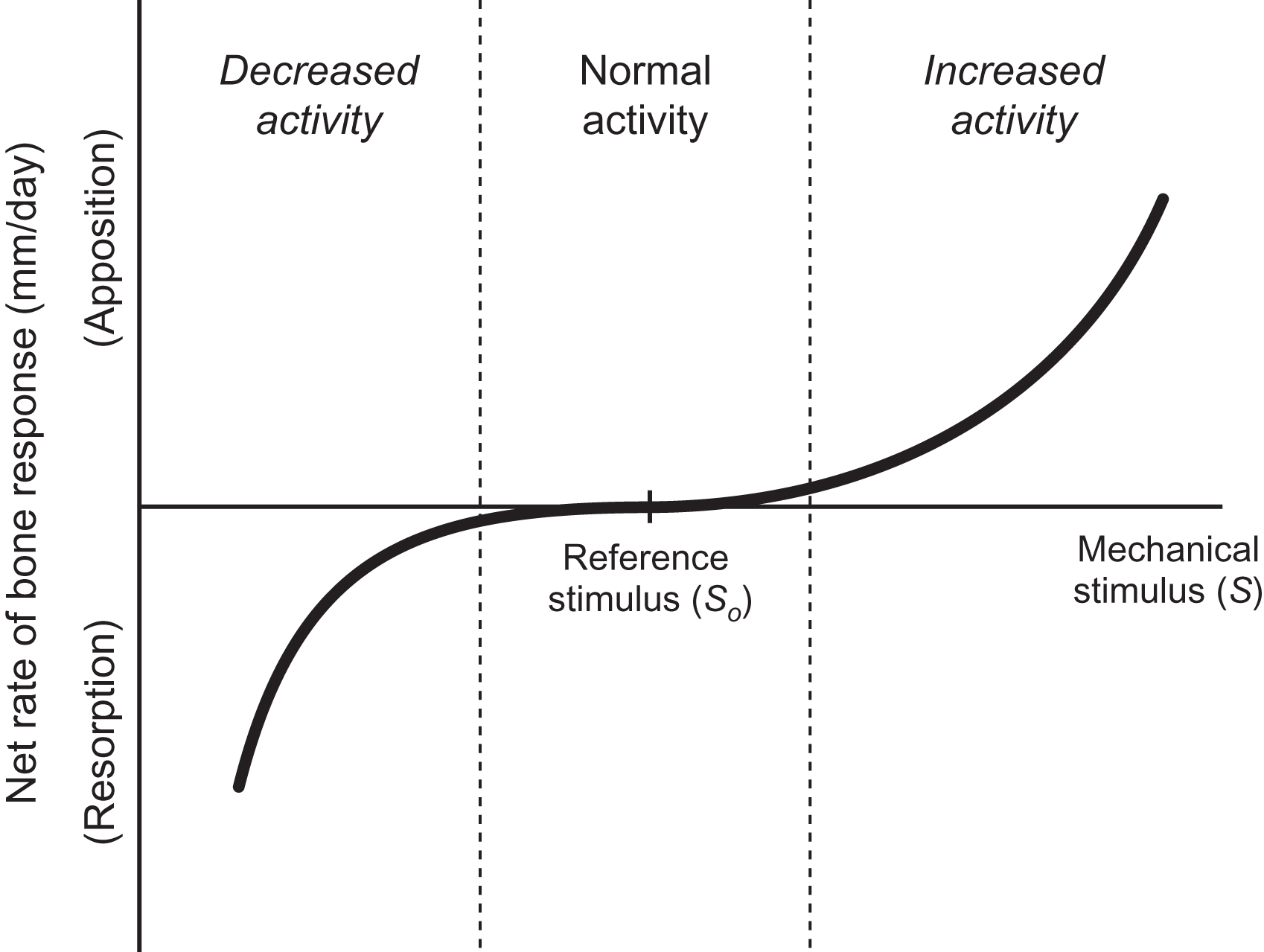
The greatest unknown in the feedback model of bone mechanotransduction is the “control logic.” Specifically, how do applied mechanical loads translate into signals to increase or decrease bone mass? Bone tissue is presumed to have a reference stimulus level ( S o ) that maintains bone mass during normal physical activity. The error between the reference and the actual stimulus ( S ) experienced at a skeletal site is the signal required to adapt the tissue and reestablish homeostasis. In its simplest form the mechanoregulatory process describes the rate of change of bone mass over time ( dM/dt ) driven by the stimulus error signal, S − S o :
where M is the bone mass, t is time, C is a constant that determines the rate of change, and ( S − S o ) is the error signal driving adaptation. Based on this type of approach, a number of groups have developed analytical and computational simulations of bone adaptation to mechanical loading at cortical and cancellous sites ( Table 15.1 ).
| Timeline of major advances in mathematical and computational modeling of functional adaptation in cancellous bone | |
|---|---|
| 1976 | “Adaptive Elasticity” constitutive model to simulate bone adaptation |
| 1984 | Functional adaptation of cancellous bone expressed in feedback diagrams |
| 1982 | The relationship between applied load and net bone formation/resorption differs among skeletal regions and has a “lazy zone” in the region of “normal” stresses/strains |
| 1987+ | Adaptation occurs in cancellous bone based on local signals (within hundreds of micrometers) |
| 1992 | Use of fabric tensor to describe alterations in cancellous bone microstructure |
| 1994 | Damage accumulation as stimulus for remodeling |
| 1995 | Simulations of reorientation of discrete trabeculae |
| 2000 | Concept that local mechanical stress/strain triggers bone formation in a resorption cavity after bone resorption has completed |
| 2001 | Simulation of individual remodeling events using dynamic bone histomorphometry data |
| 2007+ | Combination of damage accumulation and mechanical stress/strain |
Based on the straightforward relationship of Eq. (15.1) , changes in bone mass with loading can be simulated. However, several key factors influence the outcome of these simulations: the applied mechanical loading, the relationship between the loading error signal and bone mass changes expressed by the constant C in Eq. (15.1) , and the time dependency of the parameters. Furthermore, the parameters in these mechanically based simulations are influenced by a host of genetic and epigenetic factors. Contributing mechanistic factors include age, genotype, skeletal site, metabolic status, and so on. Most simulations of bone growth and adaptation assume that these mechanistic factors are at normal or steady-state levels and will not influence the outcomes.
Mechanical loads are applied to the skeleton by normal daily activities. For loading to be osteogenic, the stimulus must be dynamic or time-varying. The femur experiences dynamic loading during nearly all weight-bearing activities, including walking, rising from a chair, and stair climbing. Athletic pursuits such as jogging, running, and gymnastics impart greater loads on the skeleton, so active individuals experience greater loads than their sedentary peers. Quantitatively, the applied loading can be characterized by load magnitude, number of cycles, frequency, duration, etc. Most simulations characterize load solely in terms of magnitude, with a few formulations incorporating cycle numbers. In addition, the mechanical stimulus needs to be expressed as a tissue-level mechanical parameter that can be defined at every point in the tissue. Within bone tissue, loads induce deformations (strains) and forces (stresses), and a variety of mechanical stimuli have been used as the driving signal, including stress, strain energy density, strain gradient, and fatigue microdamage.
Once the mechanical stimulus is defined, the stimulus must be related mathematically to the rate of formation or resorption of bone. In Eq. (15.1) , this relationship is determined by constant, C , often referred to as the “rate constant.” By defining a net rate of bone response, time is introduced into Eq. (15.1) . The relationship between the mechanical stimulus and the tissue response is likely nonlinear ( Fig. 15.5 ). Implementations generally use symmetric piece-wise linear relationships . The reference stimulus defines the habitual level of mechanical stimulus for which the system is in equilibrium and bone mass does not change. Furthermore, in the range near the reference, the rate of change is small; bone mass does not change with small fluctuations in activity. Outside this normal range the rates of bone resorption or deposition increase substantially. Experimental observations suggest that the rate of bone loss is greater than the rate of new bone formation. Physiologically, these processes occur on bone surfaces of the periosteum, endosteum, intracortical space, and trabeculae. In computational models the changes in bone mass depend on whether the simulation is phenomenological or mechanistic. A phenomenological model describes net changes in bone using a surrogate measure such as bone apparent density or bone mineral density as an outcome parameter. A phenomenological model concentrates only on the changes in the surrogate measure and includes few details of the biological processes ongoing within the skeleton. A mechanistic model incorporates cell activity and signaling and could conceivably use measures of biological activity (bone formation rate and gene expression) in addition to bone apparent density or bone mineral density.
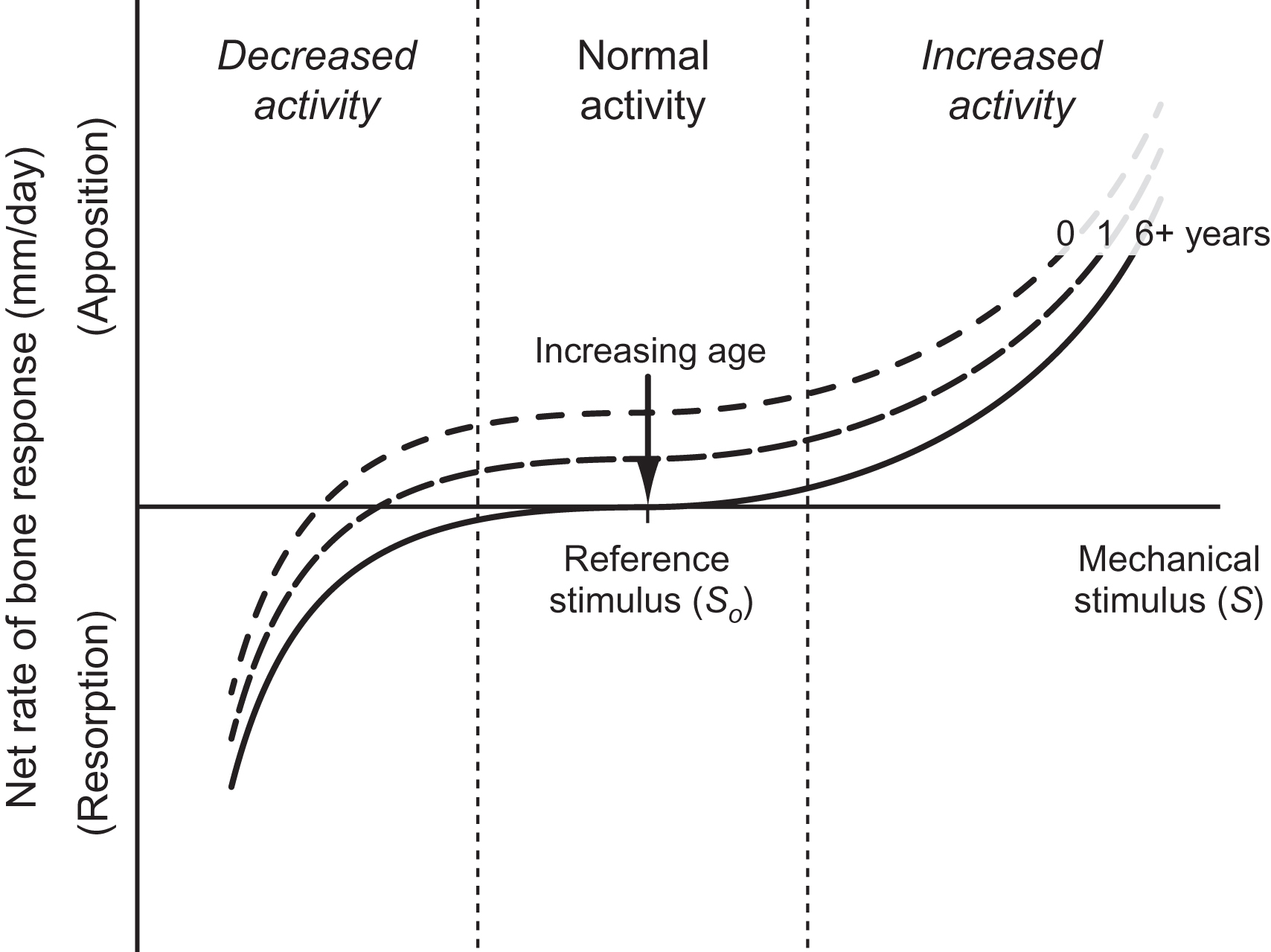
Experimentally, many parameters required to simulate functional adaptation of the skeleton vary over time. The altered mechanoresponsiveness of bone observed with aging is an obvious example. Age-related changes in mechanosensitivity could be modeled as changes in the reference stimulus, or by altering the nature of the stimulus-rate relationship. Few models account for changes in mechanoresponsiveness over time, with the exception of models simulating growth .
15.2
Diaphyseal cortical bone
The long bones perform an important structural role in the skeleton supporting body mass and enabling locomotion in Earth’s gravitational system. The response of a structure such as a long bone to applied loads depends on the properties of the constituent material (or tissue) and the geometric distribution of this material. These two characteristics will be examined individually. The cortices of the long bones consist of dense bone tissue known as cortical bone. By mass, approximately 80% of the skeleton is cortical bone. Loads applied to whole bones generate high loads within cortical bone tissue due to the moment arms created by the offset of structures such as the femoral head and tendon attachments, as well as the large bone lengths of the long bones. The ability to bear loads is a function of material and geometric properties of the whole bone (see Chapter 16 : Biomechanics of hip and vertebral fractures for discussion of bone material properties).
Because the material properties of cortical bone change little during postnatal growth, changes in femoral diaphyseal structural behavior are dominated by geometric changes. In the adult, when both material properties and geometry are relatively stable, differences in cortical structural strength and stiffness are also generally attributable to subtle geometric variations.
Long bone cross-sectional geometry is complex and varies along the bone length. Closed-form solutions to mechanical analyses, in contrast, are limited to known geometries and thus require many simplifying assumptions when applied to skeletal structures. Nonetheless, engineering beam theory provides important insights into the key determinants of mechanical performance.
The governing equations for compression, torsion, and bending relate the applied loads to the geometry and material properties for idealized rods and beams with constant cross sections and linear elastic material behavior . In general, long bones are modeled as hollow, prismatic tubes of either a circular or similar elliptical cross section . Simple geometric relationships indicative of bone structural behavior derived from the governing equations for different loading conditions can be used to understand diaphyseal structural behavior. For example, the governing equation for the torsion of a hollow circular cylinder results in the following expression for the applied torsional moment, T ,
where J is the polar moment of inertia of the circular cross section, R is the outer (periosteal) radius of the tube, and τ ult is the shear strength (or maximum shear stress) of cortical tissue. Assuming that bone material properties are relatively constant, the torsional moment withstood by a bone with cross-sectional properties R and J is proportional to the geometric term J/R . Similarly, when loaded in bending, the bending moment, M , is directly proportional to an analogous geometric term:
where I is the area moment of inertia about the bending axis and σ ult is the tensile strength (or maximum tensile stress) of cortical tissue. Finally, the compressive force, F , along the longitudinal axis of a bone is similarly proportional to combined geometry and material measures:
where A is the cross-sectional area. Because A is effectively a measure of bone mass, this force is the simplest to determine, but few skeletal sites are subjected to pure compression. In general, the tissue loads engendered by bending and torsional moments are much larger than by compression. As for more traditional man-made structures, these relationships demonstrate that the cross-sectional morphology of a long bone is critical to its ability to bear loads without failing. Experimental results show a strong correlation between bending strength and section modulus confirming this analysis (see Chapter 13 : The mechanical behavior of bone).
15.2.1
Theories of cortical bone adaptation
Development of cortical bone occurs primarily through appositional growth once the initial bone has formed by endochondral ossification. The very first bone formed is the primary bone collar deposited on the cartilage rudiment. This bone then expands with progression of the primary ossification center. Thereafter, the continued development of cortical bone form is increasingly influenced by mechanical loading, and the relative contribution of intrinsic biological growth reduces with time. Therefore this process lends itself well to mechanically based simulation, whereby expansion of the periosteal and endosteal envelopes is driven by increased loading during growth.
Computational models of cortical bone have mainly focused on adaptation of adult geometry to changes in applied loading. In nearly all cases the cortex is modeled as a symmetric hollow cylinder. Guo and Cowin used torsional loading to examine adaptation of the surface of a cylindrical model of the cortex . Similarly, Hart compared the effect of different material maturation relationships on the expansion of the periosteal and endosteal surfaces with axial compression . A recent exception is a three-dimensional geometric model of a whole rat ulna developed from a microcomputed tomography scan to simulate adaptation to loading . Surface changes were compared to experimental data using a strain energy–based stimulus and formulation similar to Eq. (15.1) for a 16-week experimental study. While time-dependent changes were examined, the model time increments were pseudo-time and did not correspond to any experimental time measures.
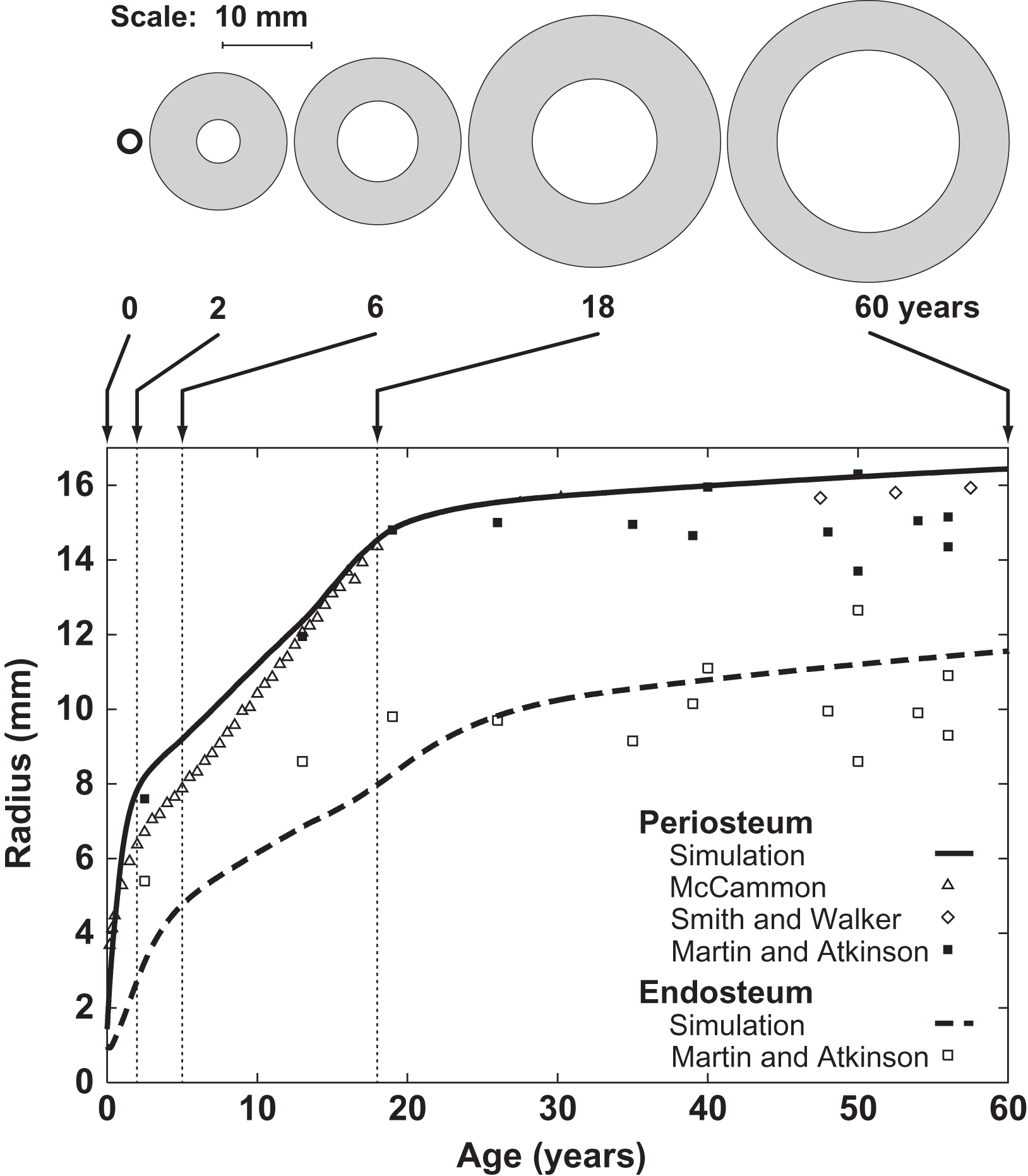
Changes in bone surfaces in the adult cortex are small and capture relatively short time periods. Few computational models of bone have included geometric expansion during growth and development of the individual. The bone adaptation algorithm formulated by Beaupré et al. for cancellous bone has been used to simulate the development and maintenance of the long bone diaphysis and then extended to include the role of periosteal surface pressures in the development of cross-sectional shape . The adaptation model of cortical growth and development captures the main features of load-based adaptation and will be detailed next. The circular diaphysis was represented by periosteal (outer) and endosteal (inner) radii and subjected to torsional loading in the form of Eq. (15.2) . The applied torsional moment increased with age and was scaled based on human body weight data during growth. The magnitude of the applied moment at maturity was calculated based on adult growth rates and applied for an equivalent of 10,000 cycles/day.
Modeling long bone cross-sectional development requires not only time-dependent changes in applied loading but also the resultant growth rates. To do so, inherent biological growth was combined with the mechanically mediated growth process described in Section 15.1.2 and governed by relationships in the form of Eq. (15.1) . For this surface-based growth, bone mass changes resulted directly in surface expansion or contraction. The responses of the periosteum and endosteum were similar except that the periosteum could not resorb. The baseline biological growth rate declined with age, reflecting the increasingly strong influence of mechanical stimuli postnatally. This approach is equivalent to varying the stimulus-rate relationship from a positive net apposition to the balanced apposition–resorption at the reference stimulus depicted in Fig. 15.5 ( Fig. 15.6 ).
Starting from an initial bone collar geometry, the model simulations found that the periosteum and endosteum expanded rapidly with growth and stabilized at maturity ( Fig. 15.7 ). Gradual periosteal expansion and thinning were present after maturity with aging despite the constant load level. The results corresponded well with diaphyseal measurements reported in the literature.
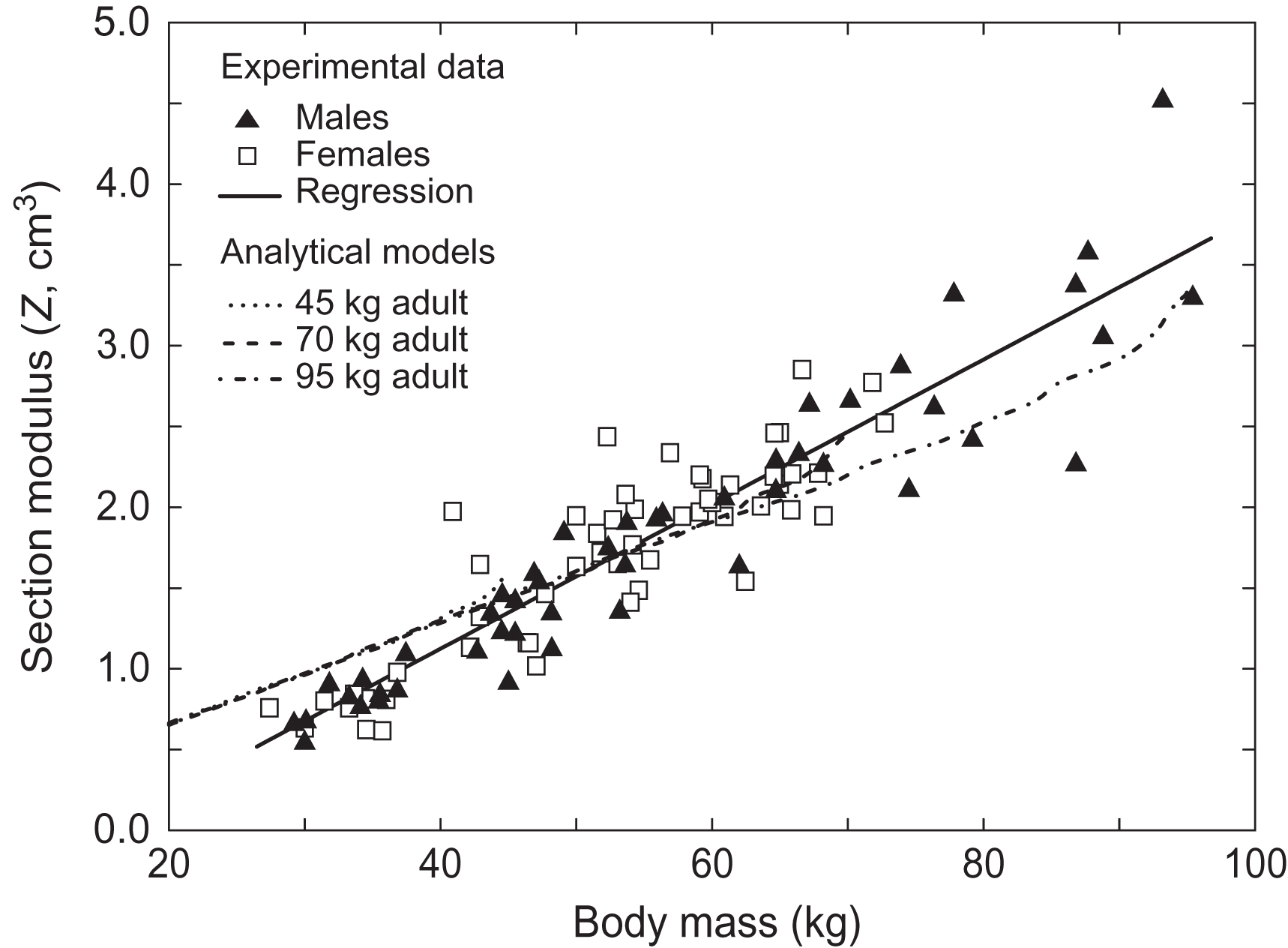
This same modeling approach was used to examine the correspondence of our model predictions with cross-sectional measurements of the human femur during adolescence and early adulthood . The experimental data set contained cross-sectional measurements from dual energy x-ray absorptiometry (DXA) scans of 101 Caucasian adolescents and young adults (age 9–26 years and body mass 29.2–94.7 kg) . For the models the range of the clinical data was represented by scaling the original simulation to capture the experimental range of body mass, resulting in developmental simulations for individuals of with 45, 70, and 95 kg body mass. The relationship between the section modulus and the experimental data was linear ( r 2 =0.86) and independent of gender. The simulations showed a similarly strong linear relationship for section modulus and body mass ( Fig. 15.8 ). The underlying hypothesis that diaphyseal structure during growth results from a biological response to mechanical loading is supported by the strong correspondence between the clinical data and model results with respect to body mass. These data demonstrate the value of computational models for exploring mechanisms behind relationships in experimental data.
15.2.2
In vivo loading of cortical bone
The in vivo effects of increased loading on cortical bone have been examined extensively in growing and adult animals and form the basis for most of our knowledge of bone mechanobiology. Cortical adaptation during growth primarily affects bone quantity with few changes reported in bone tissue quality, although relatively few studies of the changes in tissue quality have been performed. Increased bone mass results from increased cortical thickness. Bone length is generally not altered with loading in growing animals. The adult skeleton is less sensitive to loading than the immature one . Similar increases in loading produce smaller effects in the mature than the growing skeleton . At all ages, increasing bone mass with increased loading is more challenging than losing bone through reduced loading.
External loading of a skeletal site allows controlled loads to be applied while controlling for parameters such as load magnitude, number of cycles, loading rate, frequency, and duration. This control is an important advantage over conventional in vivo methods using exercise, overload by bone resection, and centrifugation to increase skeletal loads. Early implementations of controlled in vivo loading used surgically implanted hardware to apply the loads, and bone response to surgery was a confounding variable . Results from these early models demonstrated the importance of dynamic mechanical stimuli, and bone formation correlated with load magnitude in most cases.
Noninvasive in vivo models that load the entire rodent limb were developed to eliminate the potential confounding effects of surgery. Four primary models exist: four-point bending of the tibia, compression of the ulna, cantilever bending of the tibia, and compression of the tibia ( Fig. 15.9 ) . These models primarily load cortical bone, either due to the method of load application or the limited cancellous bone within the loaded site; the mouse tibia is the exception and contains a substantial volume of cancellous bone. These models have provided valuable experimental platforms to study anabolic characteristics of loading, components of the signaling pathways, and other effects associated with bone functional adaptation. Mechanistically, the response to in vivo loading is purely anabolic bone formation (modeling) and is not altered when osteoclast activity is inhibited .
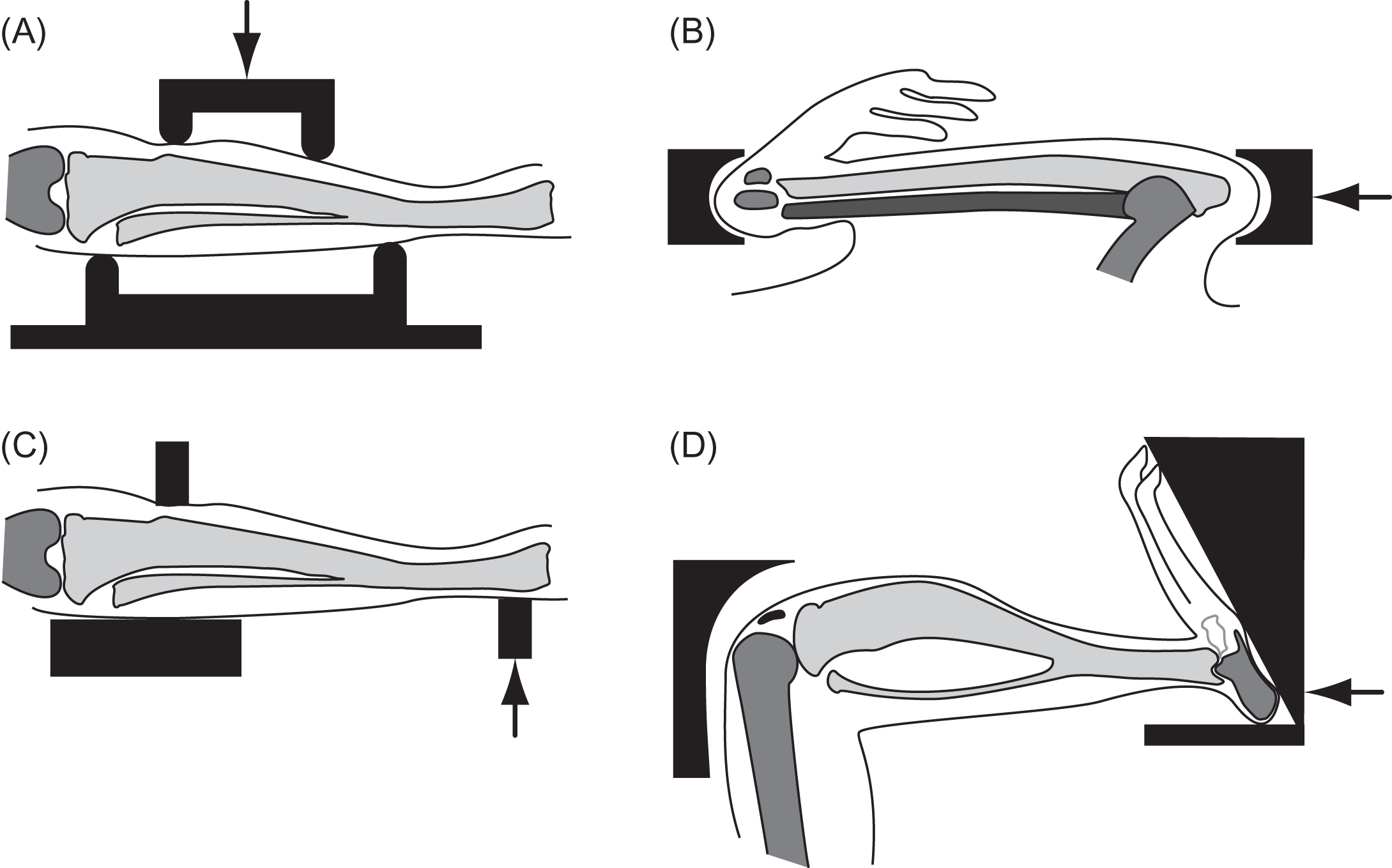
Four-point bending of the rat tibia was the first noninvasive controlled loading model to gain widespread use . Loads, applied transverse to the tibia, create bending between the inner span that loads the central cortical segment in bending. Normally, the tibia is not loaded transversely in vivo. In addition to the nonphysiological orientation of the loading, another limitation of this model is the proximity of the load points to the tissue region of interest. The latter point is critical; when the model is adjusted to apply compression to the periosteum without any bending, periosteal bone formation occurred under the load points, which led investigators to focus on the endocortical response. However, the bending stresses with loading vary radially [see Eq. (15.3) ], so the endocortical stimulus and response are less than the periosteal response, eliminating a valuable component of the model.
Concerns associated with the periosteal location and the nonphysiological nature of in vivo bending were addressed by the development of a model applying compression to the longitudinal axis of the rat ulna , which then became the most commonly used in vivo loading model. Small volumes of cancellous bone in the rodent ulna limit the analysis to cortical bone. Both the tibial bending and ulnar compression models were initially developed for the rat and then scaled down for the mouse, allowing molecular and genetic assays to be incorporated.
Cantilever bending of the rodent tibia has also been used . In contrast to the other methods that apply a constant load to a portion of the diaphysis, the applied bending moment varies linearly in this model. This model has not been adapted as widely as the others but has been a very effective tool and added considerably to our knowledge .
More recently, noninvasive in vivo compression of the mouse tibia has been developed as an alternative in vivo loading approach . A significant advantage of this model is the moderate volume of cancellous bone present in the proximal tibia, providing an opportunity to directly compare responses in the cortical diaphysis and cancellous metaphysis. The mechanical stimulus, however, will differ at the two sites. The metaphysis experiences compression, whereas substantial bending is present in the diaphysis. Bending not only increases the strain levels but also introduces substantial tension. In addition, the cartilage at the tibial growth plate and tibiofemoral joint are loaded, allowing the interaction of bone and cartilage adaptation to be examined. A limitation is that the loads are applied to the tibia through the knee joint and care must be taken to avoid damaging the joint that can occur if applied loads are too high. The highly curved length and variable noncylindrical geometry of the tibia also limit the accuracy of engineering beam theory at this site.
A potential advantage of these models is the ability to perform paired analyses by using the contralateral limb as the control. Paired analyses allow smaller differences to be detected and reduce animal numbers. For ulnar loading in the rat, most investigators present relative data, normalizing values for the loaded limb with the contralateral control value. Investigators using paired study designs should always confirm the lack of systemic effects from stimulating the loaded limb. Reactions in the contralateral control limb indicating systemic effects have been reported in the rat ulnar loading model . In the mouse, tibial loading does not induce systemic effects, when the contralateral limbs are compared to sham-loaded controls .
A key consideration for in vivo adaptation experiments, as discussed previously for computational models, is the characteristics of the loads applied to the bone, particularly when comparisons are made across animals of different gender, age, and other characteristics. Most investigators focus on the relationship between the applied loads and the strains engendered on the surface of the cortex, with an emphasis on load magnitude. Peak surface strains at the mid-diaphysis during maximal activity are similar across a variety of animals, and strain levels during normal activity are in the range of 1000–1500 µstrain . Different approaches have been taken to determine equivalence of loading magnitude. The relationship between applied load and in vivo strain can be measured by applying strain gauges to the surface of the cortex in vivo . Strain values can be matched directly for measurements taken at comparable locations across animals or combined with mechanical models to predict the maximum strains in a given cross section along the length. Applying strain gauges to the mouse cortex requires technical skill but is regularly performed. Gauge placement requires a flat surface free of muscle attachments, limiting appropriate gauge locations by length-wise and circumferential variations in tibial geometry. When data are compared across experiments, magnitude is only a single parameter of the applied loading; duration, strain rate and frequency, and strain rate of loading also need to be considered and vary considerably for different reports in the literature.
Through in vivo controlled loading experiments, the contributions of different load parameters have been compared to better characterize osteogenic stimuli for cortical bone. All in vivo loading models have demonstrated a dose response of bone formation with stimulus load magnitude . Computational models of bone adaptation assume a minimum stimulus level to elicit a formation response ( Fig. 15.4 ). A minimum load magnitude threshold for bone formation has been reported for bone formation with tibial bending . Lamellar bone formation was stimulated by loads generating tissue strains exceeding 1050 µstrain and increased in a dose-dependent fashion, but woven bone formed in response to high loads in a dose-independent fashion . A dose response is also evident for strain rate . Impact exercise combines both high load magnitudes and strain rates, so these effects are consistent with clinical data. Data for the role of the number of cycles on the response are mixed, demonstrating both a dose–response effect and saturation when more than 50 cycles are applied . The effect of the number of cycles may differ for high- and low-magnitude loads and also be influenced by other characteristics of the load waveform.
Particularly, unique results from these models include the identification of different loading paradigms. A series of studies by Robling et al. demonstrated that loading “bouts” are more effective than continually applied loading . For example, 360 cycles of daily loading enhanced bone mass and strength of the radius more when administered as 2 bouts of 180 cycles or 3 bouts of 120 cycles, rather than applying the total number of cycles in a single bout. Using cantilever bending of the tibia, bone formation has been demonstrated at low load levels that are normally insufficient to elicit a response by inserting rests between individual loading cycles . Long-term effectiveness of loading appears to decrease but resumes following time off . Combined, these results suggest a time dependency in the cellular response to loading. Mechanisms that have been suggested to contribute to this behavior include cytoskeletal reorganization.
15.3
Cancellous bone
15.3.1
Mechanics of structure
The mechanical performance of cancellous bone, like that of cortical bone, depends on bone volume, structure, and tissue material properties . Cancellous bone displays high porosity and variability in porosity across the skeleton and therefore has a more complex microarchitecture than cortical bone. As described in Chapter 16 , Biomechanics of hip and vertebral fractures, the mechanical performance of cancellous bone at the continuum scale (specimens of 3–5 mm in smallest dimension) is dominated by apparent density. Alterations in tissue properties, including degree of mineralization and collagen cross-linking, may also alter cancellous bone biomechanical performance. The number, orientation, and type (rod-like vs plate-like) of individual trabeculae can influence Young’s modulus and strength of cancellous bone independent of bone volume fraction, demonstrating that the arrangement of individual trabeculae is important to cancellous bone mechanical performance .
The theories of bone mechanobiology we have outlined (see Section 15.1.2 ) describe a relationship between the mechanical environment (stress/strain) within bone tissue and subsequent bone formation. The microstructure of cancellous bone, however, complicates expression of the mechanical environment of mineralized bone tissue at the scale of individual trabeculae (approximately 100 μm). When cancellous bone is loaded in apparent compression, some regions of the microstructure are submitted to compressive stress, while other regions are submitted to tensile stress. Large variations in the magnitude of local mechanical stress and strain are present, as evidenced by the fact that localized mechanical failure of cancellous bone occurs long before mechanical failure of the entire structure is obvious (i.e., apparent yield is reached) . In addition, local failure modes are changed fundamentally when the bone volume fraction is reduced below 20% (a common transition from healthy to osteoporotic bone), with low porosity cancellous bone displaying more bending and large deformations of individual trabeculae . Lastly, small variations in microstructure from cell activity can act as stress concentrations and promote mechanical failure, further altering regional variations in tissue stress/strain .
15.3.2
Theory of cancellous functional adaptation
The concept that bone internal and external structure adapts to physical forces was derived primarily from observations of cancellous bone microstructure. Based on observations that cancellous bone microstructure appeared to be aligned with maximum principal stresses within the whole bone, Roux et al. proposed that bone tissue would adapt to alterations in physical loading by changing cancellous bone density and trabecular orientation (Ref. translated and interpreted recently in von Meyer ). Wolff promoted the idea that mathematical laws based on physical phenomena could describe the changes in orientation of cancellous bone during growth and maturation. Computational and theoretical investigations into functional adaptation in cancellous bone have since sought to quantify the “mathematical laws.”
When considering the role of mechanical loading on the density and orientation of cancellous bone, one must consider how cancellous bone is initially formed. Cancellous bone is formed initially through endochondral ossification at the growth plate. Cell activity within the growth plate determines the rate of bone formation and is influenced by genetics, systemic hormones, blood supply, autocrine and paracrine factors released by local cells, and by mechanical stress/strain . Here, we concentrate on the role of mechanical forces in regulating bone formation in the growth plate (the signaling factors are detailed in Chapter 3 : Development of the Skeleton).
The idea that mechanical loading influences longitudinal bone growth was first proposed by Hueter and Volkmann in the late 1800s. The “Hueter–Volkmann Law,” as it is known, suggests that bone formation at the growth plate increases in response to tensile stresses and reduces in response to compressive stress. The concept has since been generalized in terms of stress invariants (a stress invariant is a single number that summarizes the stresses in all three physical directions) . Two stress invariants have been associated with endochondral bone formation in the growth plate: octahedral shear stress and hydrostatic compressive stress ( Fig. 15.10 ). Intermittent octahedral shear stresses within the growth plate are believed to increase bone growth, while intermittent hydrostatic compression is associated with maintenance of cartilage. The influence of mechanical stimulation on bone growth at the growth plate has been described with the following theoretical relationship :
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree