Chapter Outline
Plain Language Summary 104
Introduction 104
A Brief History of Microsimulation Modeling 105
What Is Microsimulation Modeling? 105
Description of Some Available Models 106
How Modeling Is Done: The Process of Microsimulation Modeling 107
Role of Modeling 109
Strengths and Weaknesses (“Opportunities and Drawbacks”) 119
Future Directions 124
Planning Clinical Trials 124
Multilevel Modeling (“Bridging the Gap”) 125
Methodological Advances 126
Conclusion 126
Glossary 126
List of Abbreviations 127
References
Plain Language Summary
Microsimulation is a process where complex processes are modeled on computers programmed to combine information about separate components of the process into an overall picture. For breast cancer screening this means combining information about the epidemiology of breast cancer, the use and accuracy of screening to detect tumors earlier, and the response of breast cancer to treatment at different times to draw conclusions about the effect of actual or hypothetical screening programs on the frequency of occurrence of, and death from, breast cancer. In this chapter, we review the use of microsimulation to inform breast cancer screening practices and policy.
This chapter begins with a description of some existing microsimulation models and how they are developed and tested for validity. We then review the use of simulation models to provide deeper understanding of the results of clinical trials of mammography and observational data, highlighting, for example, our enhanced understanding of the relative contributions of mammography and adjuvant hormonal treatment and chemotherapy to the ongoing decline in breast cancer mortality.
A particularly important application of microsimulation is projecting the results of different strategies for using mammography. Numerous conflicting guidelines have been proposed regarding starting age, stopping age, and interval between mammograms. None of these guidelines can be directly supported by evidence because clinical trials have not used precisely those protocols, and have not provided life-long follow-up. Microsimulations fill this gap by implementing the protocols under consideration digitally, applying them to simulated women whose “breast cancer histories” mimic those of real women. In addition to providing insight into screening schedules not studied in clinical trials, microsimulations can shed light on the potential of alternative established or existing imaging techniques to improve breast cancer mortality when used in addition to, or instead of, mammography.
Microsimulations also underlie cost-effectiveness analyses of mammographic screening programs, and several examples are discussed.
This chapter continues with a discussion of the strengths and weaknesses of microsimulation as a source of understanding, and the special advantages associated with the collaborative use of multiple models. And we conclude with an outline of possible future directions.
Introduction
This book chapter focuses on the role of microsimulation modeling in evaluating the effects of breast cancer screening. We will start by giving a brief description of the history of microsimulation modeling, explaining briefly what microsimulation is, and we will give some examples of existing microsimulation models of breast cancer screening. This introduction is followed by a description of how microsimulation models are developed, including model development and model validation. Then, we describe the role of modeling in evaluating the effects of breast cancer screening by highlighting examples of the role of modeling in interpreting trials and observational studies, monitoring ongoing screening programs, and extrapolating the effects of screening to different settings, technologies, and screening schedules. Then we describe some of the strengths and weaknesses of using microsimulation modeling and note possible future directions.
In this chapter, we mainly discuss studies using models that have been developed specifically for breast cancer, use microsimulation modeling to evaluate the effects of breast cancer screening, use a variety of perspectives (often societal) and lengthy time horizon (often lifetime), report a variety of outcomes (eg, mortality reduction, cost-effectiveness), and compare numerous breast cancer screening scenarios (varying in invited ages, screening intervals, screening modalities) to no screening or current practice, all depending on the problem/research question that is addressed.
A Brief History of Microsimulation Modeling
Generally, Guy Orcutt, is acknowledged as providing the foundation for the field of microsimulation in 1957, by suggesting that microsimulation models consisting of “various sorts of interacting units which receive inputs and generate outputs” could be used to investigate “what would happen given specified external conditions.” However, it took some time before microsimulation modeling was widely used, mainly because of limitations in computing power and the lack of suitable data. With the rise of technology and data collection, these limitations were gradually overcome, and the use of microsimulation increased. Since then, microsimulation models have been used extensively for evaluating social and economic policies, such as income tax, social security, health benefits, or pension policies. Microsimulation of industrial processes to explore ways to improve them is also common. And microsimulation also underlies some newly popular methodologies for data analysis, specifically multiple imputation for dealing with missing data, and Metropolis-Hastings or Gibbs sampling for Bayesian data analysis.
The use of models to answer health policy questions began to evolve in the 1980s with application in a wide range of health care topics, such as hospital scheduling and organization, communicable disease, screening, costs of illness, and economic evaluation. For breast cancer screening, specifically, models were developed to extrapolate the findings of randomized trials. For example, when long-term outcomes from breast cancer screening trials were not yet available, models were used to predict the lifetime benefits, risks, and costs. Since the 1980s, the breadth of application, diversity, and complexity of model approaches have rapidly increased.
What Is Microsimulation Modeling?
According to Wikipedia, “ microsimulation (from microanalytic simulation) is a category of computerized analytical tools that perform highly detailed analysis of activities such as highway traffic flowing through an intersection, financial transactions, or pathogens spreading disease through a population. Microsimulation is often used to evaluate the effects of proposed interventions before they are implemented in the real world .”
An important/distinguishable feature of microsimulation models is that individuals (or individual components) are simulated. Typically, with microsimulation modeling, a life history is simulated for each individual using an algorithm that describes the events that make up that life history. Random draws decide if and when specific events occur. For health applications, these events typically include birth and death from other causes, as well as a model part that describes the target disease events, such as diagnosis and death from disease. Because individuals are simulated, microsimulation can produce individual-level artificial data that can be analyzed using standard statistical techniques, while population-level outcomes are obtained by aggregating individual life histories. The impact of changes in influential factors on key outcomes for subgroups as well as aggregates of the population can thus be assessed by testing “what if” scenarios. A disadvantage of microsimulation modeling is that it tends to be computationally intensive. In order to obtain stable estimates of stochastic outcomes, a large number of individuals must be simulated, particularly if small effects need to be estimated with precision.
Description of Some Available Models
To evaluate the effects of breast cancer screening several microsimulation models have been developed. We will describe some of the available microsimulation models below. A comprehensive review of all such models would be impractical, so we have selected those we feel have been most influential.
In 1980, Eddy articulated a mathematical theory of screening that closely resembles the approach used by most modern simulation models. He developed a Markov process-based simulation model, CAN*TROL, which he applied to the evaluation of cancer control policies for several cancer sites. He used his model to advise numerous countries about cancer screening programs. Although the underlying mathematical screening is similar to that used by other models reviewed in this chapter, the CAN*TROL model itself is not a microsimulation model.
One of the first microsimulation models, the “MIcrosimulation SCreening ANalysis” (MISCAN) model, was developed to examine the impact of cancer screening on morbidity and mortality. The MISCAN model was developed to evaluate mass screening for breast cancer, as well as for other types of cancers, such as cervical, prostate, and colorectal cancer. It is a microsimulation model with continuous time and discrete events that simulates a dynamic population. The simulated life histories include date of birth and age at death from other causes than the target disease, a preclinical, screen-detectable disease process, in which breast cancer progresses through states, and survival. The natural course of the disease may be influenced by screening when a preclinical lesion becomes screen-detected. Screen-detection can result in the detection of smaller tumors, which may entail a survival benefit.
Within the Cancer Intervention and Surveillance Modeling Network (CISNET), many models have been developed for different cancer sites. For breast cancer, seven models were developed and extensively discussed and compared. Six of the seven models were classified as microsimulation models and six of the seven models include a natural history component. The natural history of breast cancer is modeled with a time from birth to start of the preclinical screen detectable period (the duration of this period being known as the sojourn time), clinical diagnosis, and a period of survival that ends with either breast cancer death or death from other causes. The time of diagnosis can change if screening takes place during the preclinical screen detectable period, which, in turn, may alter the time and cause of death. In most models, therapy influences survival from time of diagnosis.
Despite the similarities, the models also differ in important ways, for example in their assumptions about sojourn time, the mechanism of screen detection, tumor characteristics at diagnosis, survival following clinical detection and survival following screen detection. Most CISNET models include ductal carcinoma in situ (DCIS), but one model includes only invasive breast cancer. Also, assumptions on nonprogression vary: several models specifically assume that some percentage of DCIS are nonprogressive; one model also assumes that some cases of small invasive cancer are nonprogressive. Some groups model breast cancer progression in discrete stages, whereas other models explicitly model continuous tumor growth. The models also differ as to whether treatment affects the hazard of death from breast cancer, results in a cure for some fraction of cases, or both.
Besides these models, many models have been developed over the past years, often to estimate the effects of breast cancer screening for specific countries, and often based on previously developed models. For example, models have been developed to determine the potential costs and effects of a breast cancer screening program for New Zealand as well as Slovenia. For both, it was explicitly stated that the model used was similar to MISCAN. In Spain, a model based on the Lee-Zelen approach (one of the CISNET models) was used to estimate the amount of overdiagnosis from breast cancer screening, as well as to estimate the cost-effectiveness of risk-based screening approaches and the cost implications of switching from film to digital mammography. A similar approach was used to estimate the cost-effectiveness of breast cancer screening in Korea. In addition, specific models have been developed to estimate overdiagnosis in France, Denmark, and the United Kingdom.
How Modeling Is Done: The Process of Microsimulation Modeling
Model Development: Conceptualization and Parameter Estimation
Most models are developed to answer specific questions and the development of a model is ideally guided by an understanding and conceptualization of the problem that is being represented. The conceptualization of the problem involves addressing factors such as the disease or condition, patient population, analytic perspective, alternative interventions, health and other outcomes, and the time horizon.
With regard to the disease or condition, typically, a single disease (eg, breast cancer) or set of closely related diseases is of interest, but sometimes it is necessary to consider multiple diseases, for example if one is interested in estimating the impact on life expectancy of changes in a factor, such as smoking, that influences risk of multiple diseases. The modeled patient population should reflect the population of interest in terms of features relevant to the decision (eg, geography and patient characteristics, including comorbid conditions, disease prevalence, and stage). Analytic perspectives commonly considered are those of the patient, the health plan or insurer, and society. With regard to the diagnostic or therapeutic actions and interventions, it is crucial to model all practical interventions and their variations, because the choice of comparators has a major impact on estimated effectiveness and efficiency, and the results are only meaningful in relation to the set of interventions considered. In addition, the specific implementations of interventions might differ across countries and often across settings or subpopulations within countries. Thus, despite the same label (eg, “breast cancer screening”), effects may differ, depending on the practice patterns in the target population area. Sources of variation include the technology used (plain film vs digital), criteria for recall and biopsy recommendations, skill level, work load, and operating point of the radiologist, and differences in the underlying epidemiology of breast cancer itself. Moreover, the benefits of screening also vary with the range of available treatments and their accessibility to the population under study. It is therefore advisable to specify the components of the intervention in detail so that users can determine how well the analysis reflects their situations. Health outcomes of the model should be directly relevant to the question posed and might include number of cases of disease, number of deaths (or deaths averted by an intervention), life years gained, quality-adjusted life years (QALYs), and costs. The time horizon of the model should be long enough to capture relevant differences in outcomes across strategies; a lifetime time horizon is often required.
In order to make the appropriate choices on all these factors the modeling team should consult widely with clinical, epidemiologic, and health services experts and stakeholders to ensure that the model represents disease processes appropriately and adequately addresses the decision problem.
Once the problem has been clearly conceptualized, conceptualizing the model is the next step. To convert the problem conceptualization into an appropriate model structure, ensuring it reflects current disease knowledge and the process modeled, several methods might be used (expert consultations, influence diagrams, concept mapping). Several problem characteristics should be considered to decide which modeling method is most appropriate: Will the model represent individuals or groups, are there interactions among individuals, what time horizon is appropriate, should time be represented as continuous or discrete, do events occur more than once, and are resource constraints to be considered?
Another dimension is how complex a model should be. The appropriate level of model complexity depends on the disease process, the scientific questions to be addressed by the model, and data available to inform model parameters. There is a tension between the simplicity of a model and the complexity of the disease process. Simpler models include fewer parameters making it more likely that model parameters can be estimated using observed data. Simpler models are easier to describe, may entail fewer assumptions, and are less likely to contain hidden errors, making them more transparent. However, more complex models can be used to address a wider range of scientific questions. One approach is to begin with relatively simple models, extending these as needed to address specific research questions.
Once the model conceptualization has been finalized, parameter estimation can begin. All models have parameters that must be estimated. In doing so, when possible, analysts should conform to evidence-based medicine principles; for example, seek to consider all evidence, rather than selectively picking values that best accord with the modeler’s preferences; use best-practice methods to avoid potential biases, as when estimating treatment effectiveness from observational sources; and employ formal evidence synthesis techniques.
Some parameters might be estimated from observed data using various analytical techniques to produce a result that will be used as a direct model input. For example, data on treatment efficacy might be used by combining results from several trials on treatment effects, and using the obtained hazard rate reduction directly in the model.
Often, other parameters have to be estimated using the model itself. Typically, unknown model parameters are estimated by optimizing the fit between simulated and observed data, using, for example, least-squares, minimum chi-square, or maximum-likelihood methods. This process is usually referred to as calibration. Typically this process is used for model parameters that quantify unobservable aspects of the process being modeled. For example, a model might include the mammographic detection probability of a preclinical tumor. Such a parameter might be estimated by optimizing fit between simulation output and observed rates of incidence of screen-detected and interval (ie, between scheduled mammograms) cancers in a clinical trial. Fitting to data is well defined when a model is built for a particular intervention, and there are one or more randomized trials in which the effects of the intervention are reported in terms of end results and intermediate outcomes, which can be compared with model predictions. When observed data comes from multiple studies and disease registries, expert judgment is required for assessing data quality and prioritizing data for their importance in fitting.
Validation
Evaluation and optimization of cancer screening programs or scenarios using modeling is only useful if the estimated harms and benefits of screening are reasonably accurate. Testing the accuracy of models, that is, model validation, is, therefore, a crucial step in any modeling study.
Previously, five main types of validation have been distinguished: face validity, verification (or internal validity), cross validity, external validity, and predictive validity. Face validity is the extent to which a model and its assumptions and applications correspond to current science and evidence, as judged by people who have expertise in the problem. In other words, face validity exists when a plain explanation of the model structure and assumptions appears reasonable to a critical audience.
Verification (or internal validity) addresses whether the model’s parts behave as intended and the model has been implemented correctly. This can, for example, be tested by assessing whether the model responds as expected in simplistic boundary conditions such as zero incidence, no other-cause mortality, no benefit from screening or treatment, and other (typically contrived) sets of input parameters where expected model results can be determined beforehand.
Cross validation involves comparing a model with others and determining the extent to which they calculate similar results. If similar results are calculated by models using different methods, confidence in the results increases, especially if the models have been developed independently.
In external validation, a model is used to simulate a real scenario, such as a clinical trial, and the predicted outcomes are compared with the real-world ones. Ideally, external validation tests the model’s ability to reproduce observed results in a validation data set that was not used as a source of parameter estimates or calibration while building the model. Given, however, that breast cancer screening models typically include parameters that vary from setting to setting, or among subpopulation groups, some of them not directly observable, it is usually difficult to completely avoid some degree of reliance on the validation data. Completely independent external validation requires that the variable aspects of screening, natural history of disease, and treatment noted in the previous section are the same as those which prevailed for the data sources from which the model was built. For this reason, external model validation of breast cancer screening models is typically imperfect. In addition, even a fully independent external validation in a single data set, or a small number of them, should not, by itself, be taken as a definitive endorsement of the model: the number of “degrees of freedom” in any model complex enough to approach a realistic data generating mechanism will always be too large for one or a handful of fits to data to confirm.
Predictive validity involves using a model to forecast events and, after some time, comparing the forecasted outcomes to the actual ones. On the one hand, predictive validation is the most desirable type of validation, as it corresponds best to the purpose of most models, which is predicting what will happen. On the other hand, the observations are by definition in the future, making it often difficult to test a models predictive validity in a sufficiently timely manner to make practical use of its results. Predictive validity can sometimes be estimated by observing the model’s performance in simulating the results of somewhat similar events in existing data sets. For example, if the question of interest concerns the outcomes associated with different intensities of screening, it may be relevant to check how well the model can reproduce the changes in incidence and mortality that occurred during a time when a similar population introduced screening and its use disseminated.
Role of Modeling
Well done randomized controlled trials (RCTs) provide the strongest possible evidence regarding the effectiveness of interventions, and high quality observational studies are the second tier. But the available evidence at any time typically leaves some important questions unanswered. Moreover, some questions cannot, in practice, be approached with these methods. RCTs may include inadequate numbers of women in age groups of interest to policy makers. The populations studied may not be sufficiently similar to those of interest to the decision maker. RCTs typically study only one or small number of protocols for screening, whereas policy makers may wish to choose among many options. The duration of follow-up is limited, so projection of long-term outcomes requires other methods. If carried out in settings where mammography is available outside of the study, the control groups may be “contaminated,” which may result in underestimation of screening effects compared to what would happen with the de novo introduction of screening. The results of an RCT may be of limited relevance if new mammographic technologies have been introduced since the trial concluded, or if the spectrum of available treatments has changed. Findings regarding subpopulations of special interest for policy may be nonexistent or underpowered.
By synthesizing the results of relevant RCTs and observational evidence, and supporting the projection of outcomes of hypothetical screening programs, models can overcome some of these limitations of RCTs and provide policy makers with information that covers a wider range of possibilities and may be more closely tailored to the prevailing circumstances in which the decision maker finds him/herself.
In the following sections, we will provide an overview of the different roles microsimulation models have had in evaluating the effects of breast cancer screening. Each category is explained and highlighted by selected examples.
Interpretation
The interpretation of observational studies, and sometimes that of clinical trials, is made difficult by the fact that in the real world, influential factors other than the object of study are often changing too. For example, during the same period that mammography screening became widely available and widely used in the United States, new forms of adjuvant therapy for breast cancer were also introduced, and the use of adjuvant chemotherapy became more common. When systematic screening programs are introduced, changes in incidence and mortality may also be influenced by concurrent changes in risk factor prevalence or treatment patterns. Differences in breast cancer outcomes between different populations can seldom be ascribed to a single cause: typically the prevalences of different risk factors, utilization and implementation of screening, and treatment patterns will all differ. Ordinary statistical analyses, such as regression equations, have at best limited ability to accommodate such confounding variables. Simulation models, however, because they can represent complicated and multifaceted data generating processes, can disentangle the concurrent effects and support attribution of portions of the observed effects to each cause by providing projections of the expected outcomes under both real and counterfactual combinations of these factors.
Trials
Several RCTs have been performed to evaluate the effects of breast cancer screening, reporting significant mortality reductions for women aged 50–69 years. For women younger than 50 years, breast cancer mortality reduction rates of 10–13% were published. However, some women in the age group under 50 were also screened when they were 50 years old or older. Part of the observed mortality reduction in these women is likely to have been a result of detecting the cancer earlier in later rounds when the women were 50 years old or older. It is, however, not directly observable how large this proportion is. Therefore, a modeling study estimated what percentage of the observed mortality reduction for women aged 40–49 years at entry into the five Swedish screening trials might be attributable to screening these women at 50 years of age or older. By simulating all Swedish trials, taking into account important trial characteristics, such as age distribution, attendance, and screening interval, it was estimated that around 70% of the 10% reduction in breast cancer mortality observed for women in their forties might be attributable to screening these women after they reach age 50.
Another example of dissecting the results of a clinical trial is Van Ravesteyn et al. applying the MISCAN model to simulate the UK Breast Screening Frequency Trial. That trial directly compared annual and triennial screening intervals. The investigators found that the difference in breast cancer mortality between the two arms was not statistically significant (RR 0.93, 9% CI 0.63–1.37), a surprising result. The trial simulation replicated the findings of the actual trial, although it produced a slightly more favorable result. The original trial followed women for 36 months. The microsimulation was used to project lifetime mortality, with no material effect on the predicted relative risk of death. However, the projected relative risk became more favorable to annual screening if full attendance of all invitees was simulated and a higher mammogram sensitivity were achieved. The investigators concluded that given actual screening conditions that prevailed during the trial, the trialists’ original expectation of a 25% breast cancer mortality reduction was overly optimistic, and consequently the study was substantially underpowered to detect the actually achievable reduction. They noted that measures to increase the sensitivity of mammography and obtain better adherence to the assigned screening schedules would have enhanced the power of the trial.
Observational data: trends
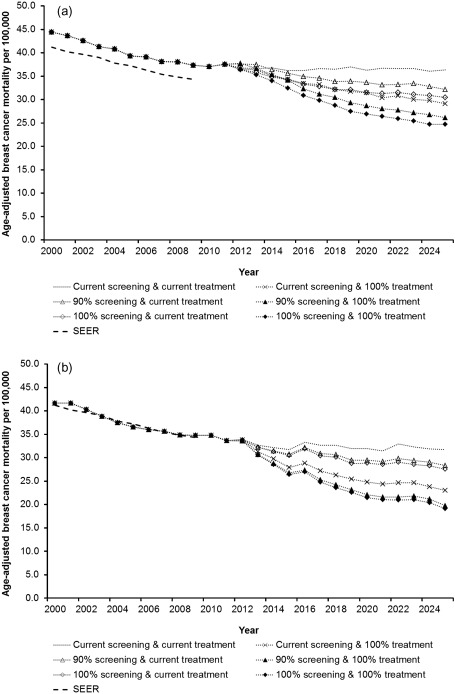
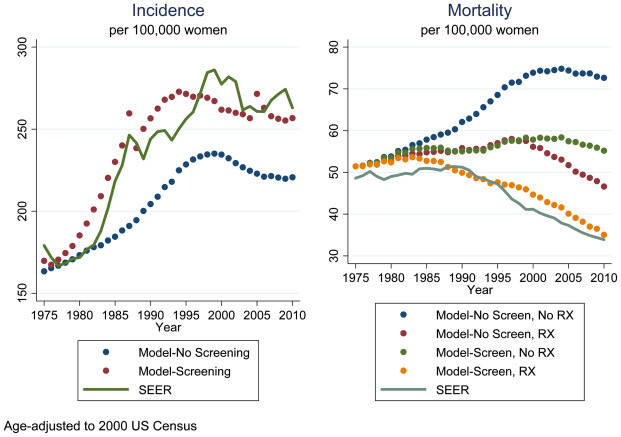
US breast cancer mortality in women aged 30–79 year decreased by 24% from 1989 to 2000. The decline was hypothesized to be due to the dissemination of screening mammography, adjuvant therapies for breast cancer, or both. Because both interventions were disseminated over approximately the same time period, it was not possible to separate the contributions of each to the mortality decline using standard techniques. Using modeling, an analysis with seven independently developed models using common inputs on utilization patterns of mammography and adjuvant therapy was conducted. This analysis was one of the first that used multiple models that shared key inputs to address the same research question. The models first calibrated their inputs and parameters to provide a reasonable approximation to SEER incidence and mortality from 1975 through 2000. They then reran the simulations, once with the screening portions of the models “turned off,” again with the adjuvant treatment portions turned off, and finally with both the screening and adjuvant treatment portions turned off. This made it possible to discern the separate impacts of screening and adjuvant treatment on modeled incidence and mortality. All models found that both screening and treatment reduced breast cancer mortality (thus, the observed reduction in breast cancer mortality could not be attributed to either factor alone), and each contributed about equally to the decline observed by 2000. Moreover, the effects were roughly additive: there was neither synergy nor interference between screening benefits and treatment improvements. The range of mortality reductions due to screening and adjuvant treatment was somewhat narrower for treatment than for screening, reflecting that the underlying evidence regarding treatment efficacy is more consistent. The approach used is illustrated in Fig. 5.1 , where a recently updated version of one model’s results is shown. Note that the mortality curves for adjuvant treatment but no screening and for screening but no adjuvant treatment diverge after 2000. This reflects the adoption of more effective forms of adjuvant chemotherapy introduced around the turn of the century. Although there have been technological improvements in breast cancer screening as well, their impact on mortality is smaller and does not appear until 2005. For this model, at least, the conclusion that screening and adjuvant treatment contribute equally to mortality reduction does not apply after 2000.
Refining the question further, six of the same seven models more recently estimated the contributions to breast cancer mortality reduction of screening in treatment separately for estrogen-receptor (ER) positive and ER negative tumors. It had long been known that ER positive and negative tumors respond differently to chemotherapy and hormonal treatments. Less widely appreciated was the difference in the rates at which these tumors grow. The interaction of these differences in treatment responsiveness and susceptibility to screen detection had not previously been examined. The models found that whereas screening and adjuvant treatment played approximately equal roles in mortality reduction from ER negative breast cancer, reduction in mortality from ER positive tumors was more attributable to adjuvant treatment. Other ER specific differences were also noted. ER negative tumors are less likely to be screen detected than ER positive tumors, but when screen detected, they attain a greater survival benefit. As a corollary, when comparing annual to biennial mammography, the incremental benefit of annual screening is predominantly seen in ER negative tumors.
An interesting problem also approached by modeling is the paradox of increased breast cancer mortality in the face of decreased incidence in African-Americans compared to United States (US) Whites. Two CISNET models undertook an investigation. Race-specific model inputs were developed that reflected known differences in age-specific incidence, distribution of biomarkers, and utilization of screening and treatment, finding that, while each of these factors contributes substantially to the observed difference in mortality, between 38% and 46% of the difference could not be explained.
Obesity impacts with breast cancer in complicated ways. Premenopausally, obesity reduces the risk of breast cancer, but postmenopausally it confers greater risk. Obese women tend to have lower breast density, and thus mammography may have higher sensitivity in this subpopulation, although this finding has been disputed. There is a tendency for oncologists to reduce dosages of adjuvant chemotherapy produced by standard formulas relying on body surface area or body weight because the recommended doses appears to be very high. Consequently the effectiveness of adjuvant chemotherapy in obese women appears to be reduced. Finally, obesity may be associated with increased mortality from other causes. Some of these associations are further confounded with racial differences, and it is natural to wonder to what extent the higher prevalence of obesity among Black women accounts for the increased breast cancer mortality they experience. These multiple influences of obesity on breast cancer, some working in opposing directions, cannot be disentangled impressionistically, and do not lend themselves to resolution through techniques such as meta-analysis of trials and observational studies. Direct simulation of the mechanisms driving breast cancer and the effects of screening and treatment offer the hope of understanding this complex situation. Chang and colleagues applied two of the CISNET breast cancer models to this problem. They concluded that obesity as a whole accounts for only a small proportion of breast cancer incidence and mortality in both Blacks and Whites, and that none of the mortality difference between the races is attributable to the difference in prevalence of obesity. An interesting feature of modeling is that it is possible to simulate the results of strategies that could not be implemented in the real world. For example, nobody seriously believes that obesity can be eradicated. But knowing what the impact of a hypothetical obesity eradication on other health problems would be would provide an upper bound on what can be achieved with intensive efforts to reduce its prevalence. The Chang study concluded that elimination of obesity would prevent more breast cancer cases among both Black and White women than any other preventive measure except possibly widespread use of tamoxifen prophylaxis by high-risk women.
Extrapolation
The ability to extrapolate beyond available direct evidence is perhaps the most important attribute of simulation models. In general, when drawing up guidelines or setting policy, the available evidence does not quite fit with the situation at hand. This is particularly true of breast cancer screening. The earliest clinical trial of mammography began in 1963, and even the more recent ones were mostly carried out in the 1990s. Since then plain film mammography technique evolved, and, more recently, new technologies were introduced. In addition, even considering all of the trials together, only a handful of different screening schedules have been actually tested. The trials, large as they were, could not focus on particular subpopulations. The trials had a limited duration: none followed patients for life, and even in those with long-term follow-up there has often been substantial uptake of screening in what was originally the control group. For all these reasons, the applicability of clinical trial results to current decisions about breast cancer screening is limited. Habbema and colleagues have noted that models will be most valuable in situations where the evidence base is substantial enough that credible models can be built based on it, but where the kind of gaps noted here remain.
Simulation models have the ability, by specifying some parameters differently, to project the outcomes that might have been seen had the circumstances of the trials been a closer match to what we currently face. While assuming that the natural history of the disease, and the mechanism of screen detection remain the same, a simulation model can examine the impact of varying starting and stopping ages, and intervals between consecutive screenings. The impact of different screening schedules in women at different levels of risk can be explored. And by modifying the assumptions about tumor sojourn times or test sensitivity, the implications of different technologies can be estimated. It is clear that it would be infeasible to study all of these issues in clinical trials.
Other protocols (screening ages, intervals)
Early clinical trials of breast cancer screening generally enrolled women past the age of 50 years. Elderly women, if not specifically excluded by protocol, participated only in small numbers. As a result, when breast cancer screening programs were adopted in Europe, and as the technology disseminated in the United States, there was variation in the starting and stopping ages recommended or implemented.
The Netherlands’ program began in 1988 with biennial screening between ages 50 and 70. By 1995, the question of raising the stopping age, which was felt not to be firmly based in evidence, arose. Using the MISCAN model, the investigators concluded that extending screening to age 80 would make sense based solely on the balance of harms and benefits, although the incremental cost-effectiveness ratio was higher than was considered proportionate at that time (£36,000/QALY).
Interest in the appropriate stopping age for mammography has remained, and little new direct evidence of the effects of screening older women has become available since then. It is clear that the major concern is that the higher competing mortality in older women puts them at increased risk for overdiagnosis. Additional concerns are the perception that breast cancer is less aggressive in older women, and that they may be at increased risk for complications from treatment. Although the last of these factors has not been explored in models, more recent modeling efforts have incorporated age-varying breast cancer natural history, and have also examined competing mortality rates that are conditional on the extent of comorbidity. Lansdorp-Vogelaar and colleagues performed a wide ranging investigation of appropriate comorbidity-dependent screening cessation ages for mammography, prostate-specific antigen testing for prostate cancer, and fecal immunochemical screening for colon cancer using several CISNET models. Interestingly, despite considerable differences in the actual levels of harms and benefits for these three cancer sites, age and comorbidity-specific harm to benefit ratios showed a remarkable level of consistency. For all three cancers, the US Preventive Services Task Force recommends ending screening, irrespective of comorbidity, at age 74. The investigators found that the same harm-benefit ratios could be obtained by stopping screening at age 66 in women with severe comorbidity, and by extending screening to age 76 in women with no comorbidity at all. (The average woman in this age range has mild comorbidity under the classification used in this study.)
An investigation using the same two breast cancer models as the Lansdorp-Vogelaar study, but with somewhat updated assumptions about screening operating characteristics and breast cancer natural history was presented to the US Preventive Services Task Force (USPSTF) for consideration, and the same conclusions were reached. The USPSTF did not, however, choose to modify its current general recommendation to stop breast cancer screening at age 74.
If the question of when to stop screening was among the first raised, the question of when to start remains the most controversial. The USPSTF reviewed its recommendations for breast cancer screening in 2009. In addition to a conventional systematic evidence review, they also considered output prepared by the CISNET models. The point of the latter was primarily to try to provide more refined recommendations about screening interval (annual vs biennial) and the consequences of screening women between ages 40 and 49. The models reviewed all estimated that biennial screening provided approximately 80% of the breast cancer mortality reduction that could be achieved with annual screening, but with about half of the associated harms. The model outputs provided direct comparison of harm-benefit ratios (using various types of harms and benefits) for a wide range of screening schedules. The USPSTF ended up reiterating support for biennial screening in all women ages 50–74, while recommending that screening decisions for women 40–49 be based on an individual weighing of the risks and benefits. These recommendations proved controversial. Among the criticisms raised were that the Task Force based its recommendations on evidence obtained using plain-film mammography, which by then was being rapidly displaced by digital mammography, and failed to consider more aggressive screening schedules in high-risk women.
For its 2015 review of breast cancer screening recommendations, the Task Force again obtained a structured evidence review as well as new modeling results. The CISNET models previously used were updated to reflect the operating characteristics of digital mammography, and were also modified to examine subpopulations with high (heterogeneously dense or extremely dense on the BIRADS scale) and low (entirely fatty or scattered fibroglandular densities on the BIRADS scale) breast density, further substratified by level of breast cancer risk due to conventional breast cancer risk factors. This demonstrates the level of complexity that can be handled by microsimulation modeling using computing resources that are now widely available. For example, high breast density both increases the risk of breast cancer and reduces the sensitivity of mammography. The other breast cancer risk factors, however, affect breast cancer risk without large changes in the accuracy of mammograms. Moreover, breast density tends to decline with age, whereas other risk factors remain relatively constant or may increase (eg, family history or personal history of benign breast biopsy). Attempting to determine the net effects of these conflicting influences from an impressionistic review of clinical trials would be challenging at best. The use of models provided clearer answers than could otherwise be obtained, and, in particular, highlighted where these effects would sufficiently alter the harm-benefit ratios of different screening schedules to support alternative recommendations for a targeted subgroup.
Other screening modalities
During the first decade of this century, digital mammography has largely replaced plain film mammography. Enthusiasm for digital mammography was enhanced by the Digital Mammographic Imaging Screening Trial (DMIST), which found that digital mammography had similar accuracy as film mammography overall and offered increased sensitivity for women with heterogeneously or extremely dense breasts, women under age 50, and premenopausal women. This enthusiasm in the clinical community was not tempered by the concurrent findings of no improvement in specificity. Nor, apparently was it tempered by the finding that switch from film to digital mammography would cost $331,000 per QALY gained. Although it is unclear if the actual cost of producing, interpreting, and archiving a digital mammogram differs greatly from that of a plain film study, insurers, including the US government’s Medicare program, generally provide higher reimbursements for the digital procedure. A comprehensive analysis of the costs of the transition from plain film to digital mammography in the United States was undertaken by Stout and colleagues. Four of the CISNET population models were used collaboratively to provide quantitative estimates of the full impact of the switch to digital mammography. They concluded that replacing plain film mammography with digital has led to increased costs with small added health benefits (extending life expectancy by 0.73 days). In an associated cost-utility analysis they concluded that the cost-effectiveness of using digital in place of plain film is sensitive to the disutility a woman places on false-positive diagnoses. A similar analysis by De Gelder et al. led to estimates that conversion to digital mammography in the Netherlands would lead to between 14% and 43% increase in overdiagnosis, depending on the assumptions made about the natural history of DCIS.
Although US health policy often is made without regard to costs, two of the CISNET models collaborated with representatives of the Centers for Disease Control and Prevention’s National Breast and Cervical Cancer Early Detection Program (NBCCEDP) to evaluate the impact of the transition to digital mammography on that program. The NBCCEDP operates under a constrained budget to provide mammograms and cervical Pap smears to low-income uninsured women aged 40–64. Because digital mammograms are more expensive, the program was faced with the possibilities of serving fewer women or providing its existing clients with less frequent screening. The guidance of the models was sought to determine how to allocate their resources so as to maximize the health benefits achieved. The study concluded that for those women screened, digital mammography led to 2–4% more life years gained. But this gain was erased and overwhelmed by the reduction in the number of women screened that the higher cost of digital necessitated, a net decrease of 22–24% fewer life years gained. However, this net loss could, in turn, be reversed by restricting screening to 2-year intervals, resulting in a net 8–13% increase in life years gained by mammography.
As mentioned above, women with high density breasts are at increased risk of developing breast cancer, and also at greater risk for false-negative mammograms. While the situation is somewhat better with digital than plain film mammography, concern remains over the adequacy of mammographic screening in these women. Recently, the notion that supplementary screening with hand-held ultrasound might improve the outlook for these women has gained popularity. Enthusiasm for this idea is sufficiently intense that at least 24 states in the United States, covering more than half the US population, have passed laws requiring that women be specifically informed if they are found to have dense breasts, and suggesting that they discuss the option of supplemental screening with their providers. Due to its widespread availability and relatively low cost, hand-held ultrasound (HHUS) is the most frequently proposed technology for supplemental screening. Sprague and colleagues applied three of the CISNET models to gain an understanding of the economic and health implications if the use of hand-held ultrasound for supplemental screening of women with dense breasts became widespread. This modeling posed some unique challenges. There are no clinical trials to demonstrate the effectiveness of HHUS in this application, so a wide range of assumptions about sensitivity and specificity of ultrasound had to be considered. Furthermore, it was not possible to assume that the sensitivity and specificity of HHUS are independent of mammographic outcome because HHUS detection of breast cancers relies on different physical properties of tumors. Consequently, the models needed to develop and calibrate an entirely independent approach to sonographic detection for these studies. The models concluded that supplemental HHUS screening of biennially screened women aged 50–74 with heterogeneously or extremely dense breasts (BIRADS c or d) after negative mammograms would gain 1.7 QALYs per 1000 women. It would also entail an additional 354 biopsies following false-positive HHUS results, and substantially raise costs. The incremental cost-effectiveness ratio was $325,000 per QALY. Restricting supplemental screening to women with extremely dense breasts (BIRADS d only) reduces this ratio to $246,000 per QALY, which is still beyond the range of widely accepted clinical preventive services.
Another approach to supplemental screening for women with dense breasts is digital breast tomosynthesis. This is an emerging technology, with two devices having so far been approved by the FDA. Early studies of this technology have indicated that the use of tomosynthesis increases detection of cancers while also reducing recalls for biopsies or further imaging. Tomography’s separation of shadows arising in different tissue planes, which may overlap and appear to be lesions or can overlap in ways that obscure lesions in mammograms, seems to be almost ideally suited to solve the problems that mammography faces in dense breasts. Lee and colleagues applied one of the CISNET models to study this in women age 50–74 with extremely dense breasts (BIRADS d). Because of the limited data on the performance of tomosynthesis in combination with digital mammography, a wide range of assumptions was tested in sensitivity analysis. They concluded that supplemental digital tomography gained 5.5 QALY per 1000 women at a cost of $70,500 per QALY. In addition they projected a 32% reduction in false-positive findings. The rather favorable ICER result was fairly robust to changes in assumptions about the performance of digital tomosynthesis. In particular, only when digital tomosynthesis is assumed to be only minimally more sensitive or specific than digital mammography does the ICER climb above $100,000 per QALY. The factor with most influence on the ICER is the actual cost of digital tomosynthesis. Their base case assumption was that a supplemental tomosynthesis procedure would cost $50. (For comparison they assumed $139 for a digital mammogram alone). Of additional interest, the ICER is only minimally dependent on the disutility that women attach to undergoing mammography and diagnostic follow-up testing. Even with pessimistic assumptions about this, the ICER remains under $90,000 per QALY.
Impact of changes in other aspects of breast cancer on screening effectiveness
The applications of modeling in the preceding subsections focused on extrapolating from available screening data to predict the impact of changes in screening schedules or technology. We turn now to an application in which the impact of changes in other aspects of breast cancer on screening effectiveness were modeled. Mandelblatt and colleagues building on earlier work about the impact of obesity trends on breast cancer epidemiology, sought to compare the effectiveness of three general approaches to breast cancer mortality reduction going forward: (1) increased screening frequency, (2) reducing undertreatment of obese women, and (3) elimination of obesity. Although the same two models had previously concluded that elimination of obesity would be an effective approach to primary prevention of breast cancer (also see section Observational data: trends), the current investigation projected that the greatest breast cancer mortality reduction for obese women would come from assuring that all received maximal chemotherapy (though this would come at the expense of increased chemotherapy toxicity). Annual screening from ages 40 through 54 and biennial screening from 55 until death in 90% of obese women would also have a substantial, but lesser, impact on breast cancer mortality. (see Fig. 5.2 .)