Inpatient Rehabilitation Units: Age and Comorbidities Are Not Relevant if Admission Fits the Mission

Diagnosis (ICD terminology)

ICD 9 cm coding

DRG coding

Disability

Flaccid hemiplegia and hemiparesis caused by a lesion of the dominant hemisphere

342.01

Multiple sclerosis

340

Hip joint replacement

V43.64

256

Examples of the confluence of ICD (9-cm version) into DRG codes. Neither coding system takes into account the disability of the patient

By “disease,” reference is made here to a biological alteration considered as lowering the person’s health status. It is well known that this biological diagnosis tells little about the disability associated to (or following, in case of subacute conditions) the disease itself, due to the intricate pathway leading from biology (ultimately, an alteration of body parts) to disability (ultimately, a decreased capacity of interaction of the whole person with the outer world) [2, 3]. On the other hand, disability itself [4] is the very reason for admission to an inpatient rehabilitation unit.

Various models of prediction of resource consumption have been proposed. Indirect costs, uniform across patients, prevail in rehabilitation units. Therefore, quite pragmatically, most models target the summary indexes of costs, i.e., the length of stay (LOS). Models have been realized (Table 54.2) in order to estimate also the expected outcome of hospitalization, in terms of severity of residual disability and/or of discharge destination (mostly, home vs. long-term institutionalization). A predictive model implies the possibility to compare observed and model-expected costs and/or outcomes, thus providing a relevant cue to the definition of both an “appropriate” admission and an efficient care.

Table 54.2

Functional grouping systems adopted in post-acute care, in the USA

Grouping system, acronym	Name	First author	Date of proposal (subsequent versions)	Dependent variable, variance explained	Main applications
FIM—FRG	Functional independence measure—function-related groups	Stineman MG	1994, 1997	Length of stay, days (log-transformed), 30%	Efficacy/efficiency study of rehab facilities. Research through National US and affiliated foreign databases
CMG	Cost measurement group	Carter J – RAND Corp. Study for the Health Care Financing Administration (now CMS), USA	2001	Total cost of inpatient stay, 30%	Prospective payment system, rehabilitation, MEDICARE program, USA
RUG	Resource utilization groups	Fries BE	1985, 1994	Nursing and therapy costs, 55%	Per-day payment, nursing homes, USA

A sketch of the main classification systems adopted in the USA for case-mix classification in the “post-acute” area. The CMG has been used since 2001 for prospective “per capita” payment (Medicare-covered admissions). The RUG system is used for per-day payment of nursing homes, only. The variance explanation summarizes the reliability of the predictions that can be made, based on the independent variables and specific algorithms, with respect to the dependent variable (e.g., days of hospital stay, cost of the whole stay, cost per day). Empirically, a 30% variance explanation is recognized as suitable to warrant an equitable reimbursement of a facility. In the EU (and, to the author’s knowledge, in all other countries), inpatient rehabilitation is still paid on a per-day basis. The same holds true for nursing homes. Local governments adopt various adjustments (based on diagnosis, functional scales, time since disability onset, and the like) aimed at taking into account the severity (hence, the expected costs) of different cases. Unlike the classification models in the USA, these adjustments do not stem from large-scale epidemiologic studies, nor they are uniform even within single countries

Not surprisingly, the most predictive models (not in force in the European Union but active in the USA) are those encasing not only a diagnostic coding but also the disability level at admission [5].

A harsh debate exists on the opportunity to include also age and comorbidity in the predictive models. The latter is a position strongly supported by gerontologists, whereas physiatrists, in general, do not agree (the reason will be given below).

54.2 Classification Systems in Rehabilitation

54.2.1 The FIM-FRG System

The widest and oldest application of a specific classification system to inpatient rehabilitation in the USA is the “CMG-cost measurement groups” system. With only minor adaptations, this is a variant to the original FIM-FRG system [6]. The FIM™ [7] (Functional Independence Measure) is the most popular (and validated) scale of independence in daily life (Fig. 54.1).

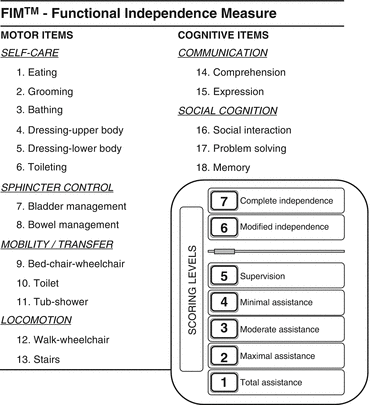
Fig. 54.1

The FIM™ scale. It rates independence in 18 activities of daily living (score 0–7, the higher the score, the better the condition). The 13 motor (total score 13–91) or the 5 cognitive (total score 5–35) items can be grouped into a “motor” and a “cognitive” subscale. Several national validated versions exist. Official teaching and credentialing procedures and authorized national data banks are foreseen, in order to preserve the national and international standardization of measures and to foster cross-cultural research

As shown in Fig. 54.1, the FIM rates 13 neuromotor (such as bladder management and locomotion) and 5 cognitive activities (such as communication and social interaction), scored 1–7, the higher the score, the greater the subject independence from aids (e.g., canes or orthotic appliances) and someone else’s help. The FIM is a worldwide standard, including rigorous scoring procedures, validated translations in several languages, dedicated courses, and a centralized credentialing exam releasing a “competency certificate.” The system also includes the diagnostic coding system RIC (Rehabilitation Impairment Codes), comprising approximately 70 macro-diagnostic categories which are function-oriented, like some codes for “stroke” or for “spinal cord lesion,” with no reference to the specific underlying pathophysiology (to compare, there are approximately 600 DRGs and almost 12000 ICD codes).

How can “diagnostic” or “functional” classes generate outcome predictions and/or indexes of appropriate admission to a health-care unit? Technically, a “decision tree” must be built. The most famous clinical decision tree is perhaps the one giving rise (“triage”) to the colored priority codes in the first aid departments. The idea is combining the patient’s biomedical “class” with other relevant information available at admission: for instance, in the case of rehabilitation, this can be gender, age, time since onset of the present disability, etc. The suspect “independent variables” may or may not be relevant determinants of the dependent variable. If they are, homogeneous “groups” can be identified, sharing a given value of that variable and presenting different values from the other groups (e.g., length of stay can be similar in patients below a given age cutoff and very different from the length of stay recorded in patients at or above the same cutoff). As a rule, however, the variables interact with each other in complex, unpredictable ways, thus giving rise to unsuspected homogeneous subgroups of patients. Figure 54.2 exemplifies (in a very simplified model) the concept of “classification systems” based on the interaction between two independent variables.

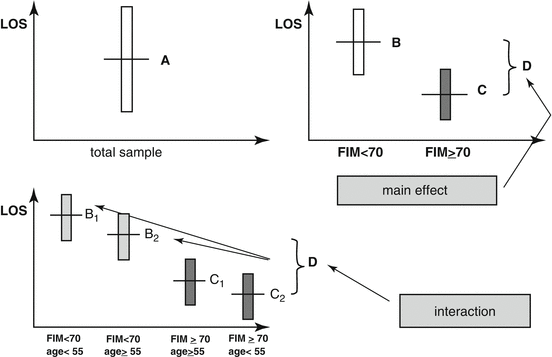
Fig. 54.2

A sketch of the “decision trees” leading to case-mix classification in inpatient rehabilitation units (after Tesio L [8]). Let us imagine that one aims at building a “classification system” predicting the length of stay (LOS, on the ordinate) based on patient’s age and his/her FIM total score at admission. In the upper left panel, the vertical bar represents the distribution (or, if one so prefers, the variance) of the observed LOS in the total sample of patients (A), the horizontal bar giving the mean. There are no “explanations” for the variance referring to the mean, which must be accepted and ascribed to chance. In the upper right panel, the sample is split into two subsamples, B and C, on the basis of the patient’s FIM score at admission (the ideal cutoff is 70 out of 126; see the abscissa). It can be seen that a large difference (D) exists between the two means, and, most importantly, that uncertainty around the mean (i.e., the variance) across each subgroup is decreased (or: some variance is now “explained”). The FIM score alone is a determinant of LOS (it represents a “main effect”). In any case, one can do better. The bottom panel shows a further splitting of the sample, based on the combination (“interaction”) of the FIM cutoff (70 out of 126) and the age cutoff of 55 years. The variance around the mean across the four subgroups is furtherly decreased. Given the FIM and the age at admission, one can reliably predict the expected LOS of the patient. If the observed LOS does not match the expectation, a diagnostic procedure can be established. The cutoff values are taken from real epidemiologic studies. Their definition and the interaction rules require dedicated statistical modeling and software [1, 8]

Only gold members can continue reading. Log In or Register to continue