Treatment Plan Evaluation

Andrew Jackson

Gerald J. Kutcher

Introduction

Interest in understanding and developing methods of plan evaluation has burgeoned over the past two decades. This has been driven in part by the development of three-dimensional (3D) treatment planning systems, and consequent introductions of 3D conformal radiation therapy (3DCRT) and intensity-modulated radiation therapy (IMRT). On the one hand, the substantial amounts of data generated by 3D planning systems have necessitated new methods of presenting and condensing the voluminous information in an understandable format. On the other hand, even with a condensed dose representation like dose-volume histograms (DVHs), the balance between tumor control and normal organ toxicity, so important, for example, in dose escalation, also needs to be addressed. Conventional evaluation of treatment plans, which judges a “best treatment plan” using tradition and practical knowledge alone, is no longer adequate to answer the issues that continually arise in modern practice. For example, should we escalate the dose to the prostate to the highest nonuniform dose or to a lower, more uniform, target dose? Can the rectum and bladder tolerate a high localized dose to a small volume? And if so, how small a volume and how high a dose? And finally, how should we balance tumor control and the risk of normal tissue complications?

In this chapter, we describe two general sets of tools for plan evaluation, one based upon physical endpoints, namely DVHs, and the other based on biologic indices, tumor control probabilities (TCPs), and normal tissue complication probabilities (NTCPs). First, we describe briefly and in schematic form the basic structure of these tools, and then describe some applications. In the penultimate section, we review the clinical data for three sites: lung, liver, and rectum.

Dose-Volume Histograms

DVHs were introduced over two decades ago (11) and are now a routine planning tool. DVHs may be represented in either differential or integral form. The former represents the volume of the organ receiving a dose within a specified dose interval, whereas the latter is defined as the volume receiving at least dose D as a function of D. The volume is either represented as the percent (or fraction) of the total volume of the organ or as the volume in cubic centimeters. The differential form lends itself well to rapid visual inspection of the range and uniformity of dose. This works well in finding cold spots in the target volume or hot spots in normal organs. The integral form facilitates the assessment of the total volume of tissue in such hot or cold spots and is the preferred format.

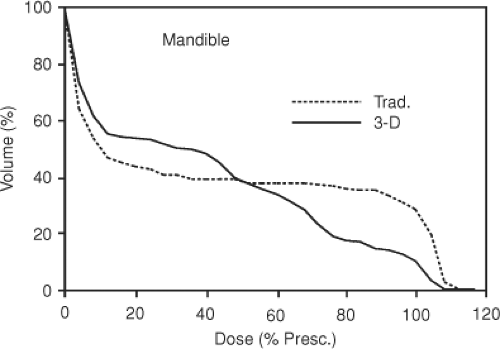
Suppose an integral DVH for plan A lies to the left of one for plan B. If the organ is a nontarget tissue, then plan A is better; if the organ is the target, then plan B is better. A more complex comparison is given in Figure 23.1 where integral DVHs for a normal organ planned with a parallel-opposed (traditional) and multifield 3D plan are shown. Although the volume irradiated to any dose level can be used to quantitatively compare the treatment plans, the location of high-dose (or other) regions cannot be determined from the DVHs. Moreover, in the example shown, the DVHs cross one another so that it is not obvious which DVH is better. This suggests augmenting DVHs to account for biologic effects.

Biologic Indices

Biologic indices represent an alternative method for evaluating treatment plans. In this section, we will describe NTCP and TCP.

Normal Tissue Complication Probability

The use of a complication probability (CP) factor to rank rival treatment plans was first discussed by Dritschilo (22). Since then, a number of techniques have been developed for estimating NTCPs. These NTCP models aim to predict the probability of a complication as a function of the dose (or biologically equivalent dose) and volume.

Existing models can be distinguished by their descriptions of the volume effect. The phenomenological model of Lyman (33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55) augmented by Kutcher and Burman (LKB)¹ seeks to describe the tolerance doses and volume effects in
terms of four parameters. In this model, partial volume tolerance doses are related to each other through a power law in volume. This implies that there is always a partial volume dose for which there is a given probability that complication will occur, no matter how small the partial volume.

Figure 23.1. Dose-volume histograms (DVHs) for the mandible. Source: Reprinted from Kutcher GJ. Quantitative plan evaluation. In: Purdy JA, Simpson LR, eds. Advances in radiation oncology physics: dosimetry, treatment planning, brachytherapy. New York, NY: American Institute of Physics, 1992:998–1021, with permission.

Other models are based on the tissue architecture of organs (88,99), with different volume effects specific to the functional organization. Serial (critical element) models assume that certain organs are organized like chains; when one link (a functional subunit) is damaged the entire chain is broken (10,11). A candidate for a serial organ is the spinal chord. Organs with this architecture have a small volume effect. For the parallel model (also called critical volume) a complication does not occur until a significant fraction of independent functional subunits (functional reserve) have been incapacitated (9,12,13,14). The volume effect in these tissues is large, because a complication does not occur if less than the functional reserve is irradiated (12,13). This behavior is not reflected in the LKB models unless augmented by an additional parameter such as a critical volume below which there is no complication. We now describe these models in more detail.

Empirical Models: Uniform Irradiation

Lyman (33) represents the NTCP for uniform partial volume irradiation of an organ with an error function of dose and volume.

The model contains four parameters: TD₅₀ (11), the tolerance dose for whole organ irradiation; m, the steepness of the dose–response curve; V_ref, the reference volume, which in some cases may be the whole volume of the organ; n, which relates the tolerance doses for uniform whole and uniform partial organ irradiation. This latter parameter represents the volume effect. When n is near unity, the volume effect is large² and when it is near zero, the volume effect is small. A value of n ∼ 1 implies that NTCP correlates with the mean dose, whereas a small volume effect implies a correlation with the peak organ dose. The NTCP for partial organ irradiation in the Lyman model was originally based on clinical estimates of partial organ tolerance doses. An early compilation by Emami et al. (15) was fitted to the model by Burman et al. (16). Although many of the parameter values he obtained are still in use, values resulting from maximum likelihood fit of DVH and complication data from 3D conformal dose escalation protocols are available for a growing list of organs. This will be described in more detail in the section on “Supporting Data for Biologic Models.”

For statistical models, described in the subsequent text, the analog of an organ with large n would be a parallel architecture organ and the analog of one with small n would be a serial organ.

Nonuniform Irradiation—Histogram Reduction and Equivalent Uniform Dose

The approach in the preceding text has been extended to inhomogeneous irradiation by converting the organ’s DVH into an “equivalent” uniform one using the effective volume method (77). The DVH is transformed into one in which the partial volume, v_eff, which is equal to or less than the whole organ volume, receives a dose equal to the peak organ dose. This effective volume transformation is self-consistent with the power law model for uniform irradiation in that it can be derived from just two hypotheses: The organ is homogeneous in response and each element of the organ obeys the same power law relationship as the whole organ. Moreover, there is a family of equivalent uniform DVHs with effective volume and dose related through the defining power law relationship. This method was extended to calculate the effective whole volume dose (d_eff) by Mohan et al. (17). More recently, use of the equivalent uniform dose (EUD) (18,19,20) has become popular. This quantity is calculated in an identical fashion to d_eff (in the EUD formalism, the LKB model parameter n is replaced by the parameter a, they are related by n = 1/a).

These models rely on clinical data, which for some organs is still quite sparse and unreliable. This is due to a number of historical factors including the inevitably poor statistics of complication data from individual treatment protocols, uncertain dose specification in the literature, lack of 3D dose
distributions, poorly specified endpoints, and poor statistical analysis. With the advent of 3DCRT, as outlined in the section on “Supporting Data for Biologic Models,” considerable improvements have been made. These include the prospective collection of dose distribution and complication data, and better statistical methods of analysis.

Statistical Models

Statistical models use binomial statistics in combination with an idea proposed by Withers (88) that normal tissues are composed of independent functioning subunits (FSUs) defined either architecturally (e.g., nephrons of the kidney) or operationally (e.g., FSUs of the skin). Moreover, it is possible to consider that tumors consist of some type (or more likely, types) of elementary units (EUs) or tumorlets as well. NTCP and TCP can then be derived in these models by considering the radiobiology of the EUs and their architectural arrangement—that is, the probability of eradicating an EU and how many need to be disabled, respectively. The former represents local dose–response and the later organ complication.

To derive NTCP/TCP we require a 3D dose distribution and a local dose–response function (12). We then derive a risk histogram, the fractional volume of the organ as a function of the probability of eradicating the EUs in that volume. Finally, we calculate the damage distribution, P(M), the probability of eradicating M and only M EUs. A generalized CP (NTCP for normal organs and 1-TCP, the recurrence probability, for tumors) is obtained by summing up the damage distribution from a lower limit L (the minimum number of eradicated EUs required to realize a complication) to N (the total number of EUs in the organ).

If L = 1, then we obtain a serial complication model where at least one EU must be eradicated. If all the EUs must be killed, L = N, then Equation 23.5 yields the recurrence probability, 1-TCP. If L is between these limits, we have a parallel complication model in which at least L EUs must be eradicated for a complication. Because the number of EUs is usually quite large, typically 10⁴ to 10⁹ (21), the derived dose–response curves will be much steeper than observed. However, if we average in some fashion over a heterogeneous population, then more realistic dose–response curves are obtained. For example, TCP calculations can be averaged over the population distribution of radiosensitivities (e.g., the distribution of the dose that controls 50% of tumors [TCD50]), whereas NTCP may be averaged over a distribution of normal organ functional reserves. Such an approach leads to models with at least four parameters, two for local response and two for the population distribution, although more may be required for the parallel model (99) and less are possible for a serial model (22). For further discussion see subsequent text and Jackson et al. (12).

Serial Organs

The description in the preceding text is somewhat formal and general. We can obtain some insight by deriving NTCP in the serial chain model. For uniform irradiation of N FSUs, the probability of eradicating at least one is given by one minus the probability of not eradicating any:

where p is the probability of eradicating a single FSU. This relationship yields a sigmoid curve of NTCP versus dose, which shifts to the left as the number of irradiated FSUs, which is proportional to the volume, increases. This serial model can be extended to nonhomogeneous irradiation (22). Moreover, while the predictions of the serial model differ from LKB models, they agree at low CP; that is the clinically significant domain.

Parallel Organs

In parallel element tissues, which have also been modeled using binomial statistics (12,13,14), a complication occurs if the fraction of eradicated FSUs exceeds a threshold fraction, the functional reserve of the organ. The kidney, liver, and lung are conjectured to behave as parallel organs. Because the number of FSUs is always large in these organs (21), the functional reserve can be defined by the fraction rather than the number of eradicated FSUs. Furthermore, as remarked before, the large number of FSUs leads to unrealistically large gradients of NTCP with dose in the region of NTCP = 50%. To remedy this population averaging is invoked, which requires additional parameters. For example, if the functional reserve and the FSU radiosensitivity (defined by the dose required for 50% FSU death) vary among a population of patients, then two additional parameters are required to represent the widths of these distributions. In addition, intraorgan variation in radiosensitivity may also be considered. Fortunately, it can be demonstrated that intraorgan variability has a negligible effect on the slope of the local dose–response curve (12).

A further simplification is possible if the width of the distribution of radiosensitivities is narrower than that of the functional reserve. In this limit the NTCP is given by the integral of the functional reserve up to the mean fraction of eradicated FSUs, that is, up to the fraction damaged (12). This form is quite useful for fitting clinical complication data as will be shown in the section on “Applications.”

NTCP models for parallel organs demonstrate a threshold effect such that a complication occurs only if at least a critical volume of the organ is irradiated to sufficient dose to eradicate the FSUs. Moreover, parallel models have a large volume effect such that NTCP correlates more closely with the mean dose rather than the peak organ dose as in the serial model. Power law models with n near unity also have a large volume effect although the functional relationship between NTCP and volume differs in detail from
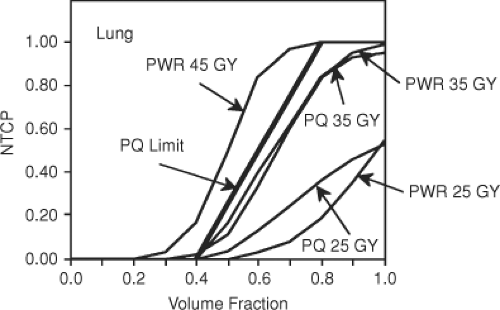
the parallel model (13). This is demonstrated in Figure 23.2, which compares calculated NTCPs for the lung for the power law and parallel models as a function of the fraction of lung uniformly irradiated to various doses. At lower doses the parallel model yields higher complications for the same fraction of irradiated lung. However, as dose is increased a limiting curve is reached, which reflects the fact that if only a fraction of the organ is irradiated, then the entire functional reserve cannot be destroyed so that the CP is less than unity. For details on this example, see Yorke et al. (13).

Figure 23.2. Normal tissue complication probabilities (NTCP) versus lung volume. PQ denotes the parallel model and PWR denotes the Lyman power law model. Source: Redrawn from Yorke ED, Kutcher GJ, Jackson A, et al. Probability of radiation-induced complications in normal tissues with parallel architecture under conditions of uniform whole or partial organ irradiation. Radiother Oncol 1993;26:226–237.

Tumor Control Probability

The central assumption of all TCP models is that a tumor is destroyed if all viable clonogenic cells within it are killed (23). From this Brahme (24) and Goitein (25) derive TCP from the product of probabilities that individual clonogens (or tumorlets) are killed. The simplest form of these models assumes that clonogens in a tumor have identical radiosensitivities and are uniformly distributed. If the dose D to each tumorlet is homogeneous and each responds independently, then TCP(v, D), the TCP for each tumorlet with partial volume v, can be inferred from the TCP for uniform irradiation of the whole tumor, TCP (1, D).

It then follows that the TCP of an inhomogeneously irradiated tumor is given by the product of tumorlet TCPs.

where TCP(v_i, D_i) is the TCP for the ith tumorlet receiving dose D_i and N is the number of tumorlets.

Several features of the model emerge immediately. The probability of controlling a tumor is dominated by any clonogens with low probability of being killed, thus TCP is very sensitive to cold spots in the dose distribution. Given the large numbers of clonogens in a tumor, when the dose is uniform the probability of destroying any individual clonogen must be very close to one for TCP to be appreciable. Given reasonable values for radiosensitivities of tumor cells, the model implies a very sharp dose response not seen in clinical studies. This discrepancy is not explainable by variations in tumor size (26,27).

Goitein and others (26,28,29,30,31,32) propose that the radiosensitivity of tumors differs from patient to patient and that the averaging over this difference results in the relatively broad dose response seen in clinical studies of TCP. Site-, stage-, and grade-specific parameters that describe the radiosensitivity of individual tumors and their variation in the patient population have been collected from clinical studies and summarized by Okunieff et al. (33). As a consequence of a distribution in radiosensitivities among patients, Zagars, Schultheiss, and Peters (32) and Thames et al. (34) point out that an escalation in dose is most effective for patients with intermediate sensitivity. Those whose tumors are most sensitive do not require such a high prescribed dose, and those who are least sensitive rarely require a dose in excess of normal tissue constraints. This implies that assays predicting radiosensitivity would be useful in identifying patients who would benefit from dose escalation.

There are other possible explanations for the discrepancy between predicted and clinical dose responses. Bentzen (29), and Bentzen and Thames (27) point out that the number of clonogens in a tumor may not scale according to the volume. Alternatively, if the number of clonogens in tumors is small, then dose–response curves will be shallow. In this case, stochastic effects arising from repopulation may need to be considered (35).

Heterogeneity in the probability of killing clonogens within a patient arises for both dosimetric and biologic reasons. Planned dose distributions in external beam radiotherapy are traditionally designed to give uniform dose distributions within the target. However, because of setup errors and organ motion, delivered dose distributions may contain unquantified cold spots that adversely affect clinical outcome. These dosimetric uncertainties cannot be accounted for at present, although efforts to measure them are underway at several institutions (36,37,38). More difficult to account for is the biologic heterogeneity of tumors. Significant variations of radiosensitivity are thought to exist within individual patients. These may arise from regions of hypoxia (39), or from genetic variation within the clonogen population. The existence of radioresistant clonogens and their location with respect to hot or cold spots in the delivered dose distribution may determine clinical outcome. Kallman et al. (40) propose a modification of the basic TCP model that attempts to account for radioresistant clonogens uniformly distributed
throughout the tumor. Not surprisingly, they find that TCP is dominated by the probability of killing the most radioresistant fraction of the clonogens. If the number of highly radioresistant clonogens is small enough, this can flatten the dose response. In addition, attempts have been made to describe the effects of variations in the density of clonogens within the tumor (41).

The uncertainty in defining tumor boundaries, uncertainty in clonogenic tumor cell densities, heterogeneous colonogen radiosensitivity, and the interaction between these uncertainties and the unknown inhomogeneities in delivered dose distributions make it difficult to test TCP models of the effects of cold spots against clinical data. Two studies attempting this indicate that the results of such efforts may be site dependent. Terahara et al. (42) studied the effects of dose inhomogeneity on local control using DVH and outcome data from 115 patients treated for skull base chordomas with combined photons and protons. In these patients, with relatively small positional uncertainties and relatively large dose inhomogeneities in the target, a Cox multivariate analysis showed that the models (including gender) and the minimum target dose were significantly associated with outcome. In contrast, Levegrun et al. (43,44) studied the effects of dose distributions and prognostic factors on biopsy outcome in a series of 132 patients treated with 3DCRT for prostate cancer. In this patient population, the clinical target volume (CTV) was defined as the prostate gland and seminal vesicles, although it is likely that the tumor clonogens were confined to subvolumes of the CTV. In addition, positional uncertainty on the order of 1 cm can be expected in the CTV location during treatment due to setup error and organ motion. The relationship between locations of cold spots in the planning target volume (PTV) and the positions of tumor clonogens was unknown. Finally in contrast with the chordoma patients, the PTV was treated relatively homogeneously. In these circumstances, the mean (but not the minimum) PTV dose was found to be significantly correlated with biopsy outcome (43), and the TCP model fits showed that there was considerable degeneracy in model parameters that were able to describe the data (44) (similar degeneracies have been found when attempting to fit such models to clinical data when DVHs were not used, see for example, Buffa et al.) (45). In an additional paper (46) studying 103 of these patients treated without hormones, the dose response was shown to be dependent on the risk group, providing evidence that the shallow dose responses seen clinically arise, at least in part, from patient heterogeneity.

Applications

We consider three applications of the models as follows:

Fitting the parallel model to clinical complication data
The application of NTCP models, in this example, v_eff, to the design of dose escalation studies
The evaluation of target dose distributions using the TCP model

Fitting the Parallel Model to Clinical Complication Data

Biophysical models can be used to try to fit clinical data. Such an approach is a starting point to suggest further developments in the collection and analysis of clinical data. We describe here one example in which a parallel model (described in preceding text) and the method of maximum likelihood is used to fit DVHs and complication data for radiation hepatitis of 93 patients treated for tumors of the liver (47,48,49).

The method of maximum likelihood can be applied as follows. The DVH³ for each patient is used to calculate NTCP by first assigning a best guess for the model parameters. The predicted probability of a complication for each patient is then compared against the observed grade of complication in that patient. The overall likelihood L of the observations is then modeled according to:

Only gold members can continue reading. Log In or Register to continue