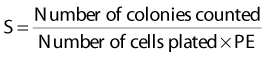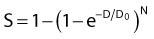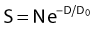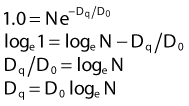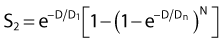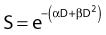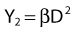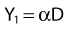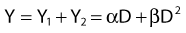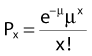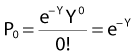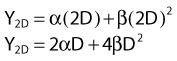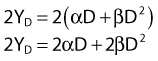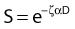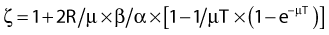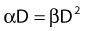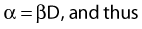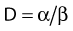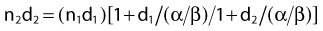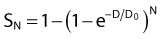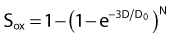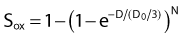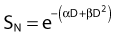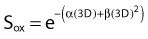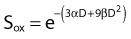Fundamental Radiobiology

X-rays and gamma rays interact with biologic material primarily by the Compton effect, producing energetic recoil electrons that traverse the cell and induce ionization events along their tracks by removing orbital electrons, either from critical molecules in the cell (direct effect) or from water molecules located 3 to 5 nm from the critical molecules (indirect effect).¹ The direct and indirect effects produce highly reactive oxygen and nitrogen species (ROS/RNS, or free radicals), which subsequently diffuse and result in further biologic damage.² By the mid-1950s, studies on the various radiation syndromes in mammals following whole or partial body irradiation had led Quastler³ to conclude that these biologic effects resulted directly from damage to the reproductive capacity of individual stem cells that were responsible for cell renewal in the irradiated tissues. Earlier work on cell killing in bacteria, yeast, and protozoa had found that single acute x-ray doses in the range of 10 to 100 Gy were required to destroy the reproductive integrity of approximately 50% of the cells. This finding led many investigators to erroneously conclude that a similar cell-killing process involving the loss of reproductive integrity was unlikely to account for tissue effects in mammals, including humans, because in mammals these effects were observed after a radiation dose of only a few Gy. If the radiosensitivities of mammalian cell were similar to the radiosensitivities displayed by microorganisms, hardly any mammalian cells at all would lose their reproductive integrity after a few Gy. However, Quastler was able to deduce that this conclusion must be incorrect and that the radiosensitivity of mammalian cells, with respect to loss of their reproductive integrity (that is, the ability to undergo multiple cell divisions to clonally repopulate a tissue), must be much greater than that of microorganisms and did in fact underlie those effects in tissues and tumors that are of interest for radiotherapy. Furthermore, it was recognized as early as 1906 that the manifestation of radiation-induced tissue injury was expressed much earlier and more severely in tissues with rapidly dividing cells than in those with slowly dividing cells. Cell death associated with dividing cells is called mitotic-linked death, and the increase in tissue response with an increase in mitotic activity is referred to as the law of Bergonie and Tribondeau.⁴ Finally, for simplification of terminology, cell killing or cell lethality is defined as the loss of the cell’s reproductive integrity; and, conversely, cell survival is defined as the ability of the cell to undergo multiple cell divisions to form a colony after irradiation.

This chapter is devoted primarily to the cellular processes involved in mitotic-linked killing of mammalian cells and other ionizing radiation (IR)-induced cell death mechanisms. Considerable evidence supports the notion that DNA double strand breaks (DSBs), or a subset of DSBs, are the most important lesions mediating IR-induced cellular lethality. Several lines of evidence have led to this assertion. First, selectively irradiating different parts of the cell using charged particle microbeams or incorporated radionuclides showed that the most critical targets for cell inactivation reside in the nucleus.^1,5–8 Second, cells are very sensitive to killing by the induction of DSBs following incorporation of the thymidine analog ¹²⁵iododeoxyuridine (¹²⁵IdU) into the DNA,^6,8 which produces approximately one DSB (or several clustered DSBs) per decay depending on local chromatin topography.^9–11 Third, cells are radiosensitized for both cell killing and chromosomal aberration induction by incorporation of the thymidine analog bromodeoxyuridine (BrdU) into DNA,^12,13 with the increase in aberrations occurring only where the BrdU incorporates into DNA.^14,15 Fourth, and perhaps most importantly, cells that are genetically deficient in rejoining DNA DSBs are very hypersensitive to cell killing and chromosomal aberration induction by IR (discussed further later and in Chapter 2). Details of radiation chemistry, the enzymology of DNA repair, and a discussion of the ongoing studies of DNA repair genes are briefly discussed later and in more detail in other parts of this book, as well as in many reviews.^16–19 The mutagenic and carcinogenic effects of radiation, which can induce secondary neoplasms following radiotherapy (RT) of the primary tumor, are not discussed, nor are they important aspects of therapeutic gain, which is defined as achieving a greater effect of radiation on tumors than on surrounding normal tissues.

The First Survival Curves for Mammalian Cells

At about the same time Quastler was reaching the conclusions described in the preceding section, Puck and Marcus^20,21 made several important observations about the radiosensitivity of mammalian cells. First, they demonstrated that mammalian cells in culture are at least one or two orders of magnitude more sensitive to ionizing radiation than microorganisms, and that the doses sufficient to kill 50% of the animals (LD₅₀) from hematopoietic or intestinal damage might be killing upwards of 95% to 99% of the stem cells responsible for cell renewal in bone marrow and gut. Second, they showed that even though IR-sterilized cells could not proliferate to form macroscopic colonies, virtually all the cells they studied succeeded in completing at least one, often two to three, and sometimes even four to five abortive divisions before proliferation ceased for doses up to a few Gy, and these often formed giant cells that remained metabolically alive but were reproductively dead. Tolmach later showed that these nonclonogenic cells disappear from irradiated cultures with a half time of about a week.²² Third, Puck and Marcus noted that functions other than reproductive capacity, such as the ability to metabolize nutrients or even the complex processes necessary to reproduce viruses, were largely unaffected by doses of even tens or hundreds of Gy. Fourth, they suggested that chromosomal aberrations induced by radiation were somehow responsible for the killing, based on, among other things, observations that these aberrations began to appear in some cells at the lowest doses at which killing first began to be measurable, and presumably at doses where the most vulnerable of cell processes would be affected.

Puck and Marcus published the first IR dose–response curve for mammalian cell killing for HeLa human cervical adenocarcinoma cells,²⁰ which is reproduced in Fig. 1-1A. In general, to obtain such survival curves, single-cell suspensions are prepared and known numbers of cells are inoculated into cell culture dishes containing the appropriate growth medium. Adherent cells then settle to the bottom, where they attach firmly to the dish. Without irradiation, inoculation of 100 single cells into a dish will yield ≤100 macroscopic colonies, with each colony containing thousands of cells that divided from these single cells following incubation for 1 to 2 weeks. This fraction of colony-forming cells in the unirradiated or untreated cultures is known as the plating (or cloning) efficiency (PE) and is often expressed as a percentage rather than as a fraction. Plating efficiencies for various tumor and normal cells are typically in the 40% to 90% range, although the system works reasonably well for plating efficiencies between 10% and 40%. Below 10%, the cells surviving without treatment may not be representative of the clonogenic population if the plating procedure itself either has sensitized the cells to IR or plating has selectively killed a subpopulation of cells, so caution should be exercised to rule out the influence of such artifacts. Irradiated cultures show reduced fractional survival values relative to unirradiated control cultures. For high doses of irradiation corresponding to survival values of 1% or less, no surviving colonies would be observed for 100 cells inoculated. Therefore, for high doses leading to low survival, the number of cells inoculated per dish is usually increased. The relative surviving fraction S is calculated as:

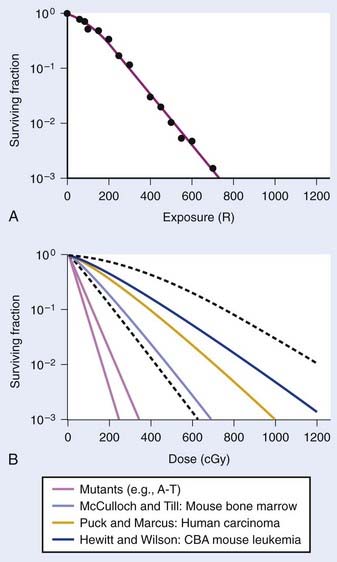
FIGURE 1-1 • X-ray or gamma ray dose–survival curves for mammalian cells. A, The first such survival curve (for HeLa cervical adenocarcinoma cells) reported in 1956 by Puck and Marcus.²⁰ B, A range of survival curves for other mammalian cells. The dashed lines encompass the range for wild-type cells of various origins. The steepest curves show a range typical of hypersensitive mutants, such as cells from patients with ataxia-telangiectasia (A-T). Note that in A, the dose is expressed in roentgens (R), which for the cells X-irradiated on glass, must be multiplied by ∼1.4 to obtain the dose in cGy.

For large IR doses that yield low survival values or cultures with very low plating efficiencies for which large numbers of cells must be plated, appropriate controls using irradiated nonclonogenic feeder cells should be used to maintain a constant cell density and ensure that variations in survival because of differences in cell density in these cultures do not occur.²³ Note that the survival curve illustrated in Fig. 1-1A, like many others, have a characteristic shoulder region at low doses; the reduction in survival per unit dose (i.e., the slope of the survival curve) is usually less than the approximately constant slope for survival values below about 0.1. Another interesting finding from these and subsequent studies was that cell populations derived from single cells surviving high radiation doses were not radioresistant, but had essentially the same radiosensitivity as the original parent populations. In fact, in many cases, populations derived from single cells surviving high doses of radiation have been found to be slightly more radiosensitive than the original population.^24,25 This finding may relate to the observation that progeny of cells surviving irradiation divide at a reduced rate and have genetic instabilities^26,27 and reduced plating efficiencies.²⁴

Subsequent to these initial survival studies that used cultured tumor cells, cells from human normal tissues were next to be studied, and other techniques and methods were devised to measure survival of both normal and tumor cells in in vivo experimental animal models. Hewitt and Wilson devised an ingenious dilution assay method to determine the dose response for cell killing in a transplantable murine lymphocytic leukemia.²⁸ They found that, on average, only two cells were necessary to induce a tumor in recipient mice. This corresponds to the inflection point on the titration curve relating the percent of injected animals that develop tumors to the number of cells injected per animal. The number, or dose, of cells for 50% tumor take is known as the TD₅₀. Hewitt and Wilson reasoned that if a radiation treatment killed half of the cells, for example, then an injection of twice as many cells would be required to transplant the tumor. In other words, the inflection point or TD₅₀ of the titration curve would be shifted from two cells for an unirradiated tumor to four cells for an irradiated tumor in which half the cells were killed. Thus, a radiation dose survival curve could be constructed by dividing the TD₅₀ for unirradiated tumors (derived from unirradiated transplanted cells) by the TD₅₀ for tumor cells receiving various radiation doses before inoculation. The survival curve the authors obtained for mouse lymphocytic leukemia cells,²⁸ shown in Fig. 1-1B, was similar to the curve Puck obtained with HeLa cells.

At about the same time the results of Hewitt and Wilson were published for mouse tumor cells in vivo, Till and McCulloch²⁹ reported an equally clever technique for assaying the survival of normal mouse hematopoietic cells. In mice (and humans), both the spleen and the bone marrow are major hematopoietic organs. The authors noticed that colonies arising from surviving cells could easily be seen as nodules in the spleen during necropsies of mice euthanized at various times after irradiation. For high IR doses, no such colonies could be seen; however, injection of nucleated bone marrow cells from unirradiated mice could rescue the irradiated mice if the doses were not too high, and some of the injected cells were also found to lodge in the spleen and form nodules. The number of these nodules was directly proportional to the number of cells injected. Thus, the spleens of the supralethally-irradiated mice acted as in vivo culture dishes in which colonies could be counted, and the injection of irradiated cells resulted in proportionally fewer colonies in the spleen. Survival curves constructed in this way using normal hematopoietic cells injected into mice were again similar to those for human HeLa cells and mouse leukemia cells, as also shown in Fig. 1-1B. These hematopoietic cells responsible for generating spleen colonies have been loosely termed stem cells, although more recent work with cell lineages in the hematopoietic system suggest that such spleen colonies are likely generated by surviving hematopoietic progenitor cells. These are sometimes referred to as spleen colony forming units (CFUs) to avoid implying a precise knowledge of their origin.

These early studies (and several others immediately following) pointed to a general conclusion that the radiosensitivities of mammalian cells examined were quantitatively similar, at least of the same order of magnitude. Doses differed by only factors of about two to three to reach equitoxic survival levels for various cells studied, but no striking systematic differences were observed in relation for tumor cells versus normal cells or those derived from rodents or humans. The range of dose–survival responses for x-rays or gamma rays delivered at high dose rates (20 to 2000 cGy/min) is shown by the dashed curves in Fig. 1-1B. It is noteworthy that although the majority of reports describing dose–survival responses for a wide variety of cells were carried out using in vitro (ex vivo) culture systems, the in vivo studies of Hewitt and Wilson and Till and McCulloch were not the only ones addressing the question of radiosensitivity of cells in more native in vivo tumor or normal tissue contexts. For example, Withers and coworkers, Gould and Clifton and coworkers, and others, have determined dose responses for in vivo IR-induced cell killing in a variety of tissues, including skin cells (D₀ ∼1.4 Gy),³⁰ crypt cells of the jejunum (D₀ ∼1.4 Gy),^31,32 testes spermatogonial stem cells (D₀ ∼1.7 Gy) (³³), kidney tubule-regenerating cells (D₀ ∼1.5 Gy) (³⁴), mammary ductal cells (D₀ ∼1.3 Gy),³⁵ and thyroid cells (D₀ ∼2 Gy).³⁶ At least for these cell types, the native tissue context does not seem to alter their radiosensitivity relative to typical mammalian cell radiosensitivities documented in vitro.

The previous observations, however, do not rule out potentially important roles for tumor or tissue-specific signaling factors and the local microenvironment in altering tissue IR responses (discussed by Barcellos-Hoff et al.³⁷). It was also recognized at a fairly early stage in the development of modern cellular radiobiology that there were consistent differences among cell types. Cells of lymphoid origin (normal or tumor) appear to be somewhat more radiosensitive than cells from other tissues. It is also important to note that virtually all of the early studies focused on single acute (high dose–rate) exposures, and radiosensitivity was judged largely by examination of survival curves in the 5 to 15 Gy range. In the past 25 years or so, it has become better appreciated that cellular responses in the first decade of survival are not only pertinent for standard multifraction radiotherapy regimens but also can reveal important systematic differences underlying cellular radiosensitivity, especially for cells exposed to low doses or low dose–rates.³⁸ The surviving fraction after 2 Gy or SF₂ is an index of radiosensitivity that has been widely used.^39,40 Recently though, the clinical use of single-fraction (or two to three large-fraction) high-dose radiotherapy referred to as stereotactic body radiotherapy (SBRT)⁴¹ has received much attention and renewed interest in the survival responses of both normal and tumor cells following doses of 15 to 30+ Gy.⁴² The role of tumor and normal tissue cell killing and therapeutic gain following SBRT are briefly discussed later in this chapter in the apoptosis section.

Definitions and Descriptions of Radiosensitivity: N’s, D₀’s, α’s and β’s

Typical IR cell survival curves are constructed with survival plotted on a log scale against dose on a linear scale (typically in cGy or Gy; where 1 Gy = 1 J/kg and 1 cGy = 1 rad), and are characterized by an initial shoulder followed by a linear (or relatively linear) portion at higher doses (see Fig. 1-1). Much effort, thought, and ingenuity in the early days of radiobiology have gone into devising mathematical models to describe the shapes of cell survival curves, based on certain assumptions including mechanisms of cell killing. With appropriate adjustment of various parameters, many mutually exclusive models of radiation action adequately fit any given set of experimental data, so curve fits by themselves tell us essentially nothing about underlying radiobiologic mechanisms. Still, they are useful, principally, in two ways. First, these mathematical descriptions of survival curves provide a very helpful way to catalog and compare radiosensitivities for different cells and different irradiation conditions in terms of these descriptive parameters, so long as one uses the same general mathematical description to fit the survival data. Second, these mathematical survival curve descriptions are useful for predicting the way cell survival may change for different radiation conditions, including changes in dose-rate or dose-fractionation, modification of the chemical environment during irradiation, or changes in radiation quality (linear energy transfer [LET]). Differences in survival may also occur because of alterations in the proportion of various subpopulations of cells that have different radiosensitivities (such as that observed as cells progress through the cell cycle, discussed later).

Historically, the mathematical descriptions of dose–survival curves most widely used for mammalian cells were borrowed from target theory, an analytical approach whose development began in the 1920s and whose aim was to deduce the size and number of critical targets in cells in which IR-induced damage led to a biologic effect. The need for such a target concept, in which damaging ionization events or ion clusters of ∼100 eV are deposited in critical structures such as nuclear DNA, stems from the fact that the amount of energy deposited by exposure to 10 Gy, which kills about 99% of the cells, would raise the temperature of the target material by only about 0.002° C.¹ Thus, the difference is that for IR exposures, relatively large amounts of energy are deposited in very small volumes (sufficient to break chemical bonds), whereas raising the temperature only increases the overall average kinetic energy of the molecules in the absorbing material slightly. It has been widely appreciated that a number of complicating factors make classical target theory largely impractical and inappropriate to describe the molecular mechanisms underlying cell killing. The original hit hypothesis and its development to the so-called target theory dealt mainly with numbers of hits or targets and their distribution among cells, and did not account for complications like heterogeneity of sensitivity within a cell population or to repair processes. More realistically, we can think of the distribution of events or hits that could be lethal and are not processed properly or are misrepaired to leave a lethal lesion some time after an exposure, rather that within milliseconds after exposure.

Although the complications effectively defeat the original aims of target theory, the mathematical dose–survival expressions from target theory reasonably fit observed dose–survival data and have been very useful for descriptive purposes. The simplest of these is of the form:

(1)

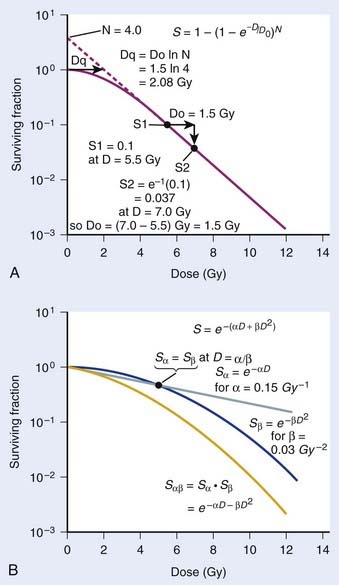
where S is the fraction of cells surviving a dose, D. This type of survival curve is illustrated in Fig. 1-2A. In this expression, D₀ is the dose on the straight-line portion of the log-linear survival plot necessary to reduce the survival from some value S to (e⁻¹ S) or (0.368 S). It is also sometimes called the mean lethal dose because it is the dose necessary to produce an average of one event per target in a cell containing N targets, all of which must be hit to kill the cell. If N–1 of these targets have already been hit, as would be the case in virtually all the cells not yet killed after a dose corresponding to survival values below about 0.1, an additional dose of D₀ would leave an average of one hit in the previously nonhit targets and would thus reduce the survival from S to (e⁻¹ S). The number N, which in this case is the number of targets, can be obtained by extrapolating the high dose, low survival portion of the curve to its intercept on the ordinate at zero dose. This value is more appropriately referred to as the extrapolation number rather than the target number, since the ideal situation in which the two are the same is seldom if ever seen in practice. It is easy to see, however, that the extrapolation number is a measure of the size or width of the shoulder of the survival curve. Another measure is the quasithreshold dose or D_q which is the intercept of the extrapolated high dose, low survival portion (below 0.1 survival) of the curve back to the dose axis drawn through the ordinate survival axis at a surviving fraction of 1.0. Another way to determine D_q is to recognize that the equation for the high dose portion of the curve is approximated very closely by:

FIGURE 1-2 • Different mathematical expressions relating radiation dose to cell survival and the parameters commonly used to characterize cellular radiosensitivity. A, Illustration of a form of the so-called N–D₀ model and how N, D₀, and D_q are calculated or estimated from such a curve. B, Illustration of the α/β model in which cell killing occurs by either a single-event process or a double-event process such that the overall killing by either process is the product of the two, and the α/β ratio is the dose at which both processes contribute equally to the total killing, i.e., the dose corresponding to the intersection of the two upper curves. Note that the upper curve is survival for the α component only, the middle curve is for the β component only, and the lower curve is for both the α and β components.

Thus, for a surviving fraction of 1.0 corresponding to the Dq dose:

(2)

To actually determine the D₀ from the straight-line portion of the curve fitted to a set of data, for practical purposes it is much easier to divide the dose (D₁₀) necessary to reduce survival by a factor of 10 (e.g., from ∼0.1 to 0.01) by 2.3 (where loge10 = 2.3) than to work out directly the dose necessary on the strait line portion of the dose versus log survival plot to reduce the survival from some value f to a value of e^–1 (f) or 0.368 (f). Thus, log_e 0.1 = −D₁₀/D₀; −2.3 = −D₁₀/D₀, and D₀ = D₁₀/2.3. Also, D₀ values cannot be estimated very well for data extending over only one log of survival (to 0.1 or above) unless the curve has an extrapolation number very near 1.0. Furthermore, for comparisons of radiosensitivities of different cells or different radiation conditions, survival data over the same dose range are often used for the comparisons, either as estimates of D₀ or as ratios of survival for a given dose, when in fact, comparisons of D₀ values should be made over the same survival range. However, if one curve extends over only one log or decade of survival while the other extends over three logs, for example, the comparison should be focused on the first decade for both curves, ignoring the second and third decades; in this case, the comparison can be the ratio of doses, called a dose modifying factor for isosurvival, or survival values for 2 Gy for example.

By far the main drawback for using the so-called simple multitarget expression (equation 1) is the fact that it usually gives a very poor fit to survival data in the shoulder region, that is, in upper part of the first decade of survival. This is a problem because, as already mentioned, the first decade (in the shoulder region) is the region of the curve that is of special interest for radiotherapy delivered in multiple 2-Gy fractions. The shape of the single acute dose survival curve below about the 0.1 survival fraction is of little interest for this purpose, though for single high dose fraction radiotherapy it certainly is of interest. The multitarget-type curve has zero slope at zero dose, and data indicates that survival curves with large shoulders do not fit the multitarget expression well at low doses (below 2 to 3 Gy). As well as providing better consistency for other considerations such as dose-rate and fractionation effects, better curve fits are obtained by adding a single-hit component to the expression, giving:

(3)

Another mathematical approach to the description of dose–survival relationships which lends itself to analyses involving changes in dose rate and or other modifying factors, and which has other appealing features, is the so-called α–β model. In this model, survival follows the expression shown in Fig. 1-2B:

(4)

One of the several appealing features mentioned earlier is that this model readily derives from a mechanism of cell killing that we now know to be largely correct, although for some cells, additional mechanisms such as apoptosis also contribute to cell killing (see later). The mathematics amounts to a simple description of the dose response for the formation of chromosomal aberrations, rather than some abstract targets of obscure identity and behavior. The model derives from the fact that cells die largely as a result of loss of genetic information in the progeny of cells bearing certain chromosomal aberrations induced by radiation. This is not just one of a number of plausible mechanisms of cell killing, but there is a large body of evidence to support it.^21,43–48 Not only has quantitative agreement been found between chromosome aberration induction and cell killing, but the strongest possible evidence is that provided by Revell and associates,⁴⁹ who showed that virtually every diploid cell of the types they studied irradiated in G1 and reaching the first mitosis with a fragment-generating (micronucleus-generating) aberration failed to form a colony, while every irradiated cell reaching the first mitosis without such an aberration did form a colony. Virtually all the cells they studied did reach the first mitosis. If these aberrations and the putative lethal events were unrelated in a cause-and-effect sense, and some other unseen lesions with the same radiosensitivity for its production were actually the real lethal lesion, then some cells with aberrations should have formed colonies while some cells without aberrations should not. The latter was not observed. As already mentioned other mechanisms of cell killing such as apoptosis, may contribute to cell killing to a greater or lesser extent depending on the circumstances (mainly the cell type). For some agents and particular hormonal induction processes, apoptosis may account for all of the cell death; but for exposure to ionizing radiation, most cells die principally as a result of the production of certain chromosomal aberrations. Apoptosis, when it is involved does not nullify the lethal effects of these aberrations in cells bearing them, but only adds to the overall lethality when it is involved.

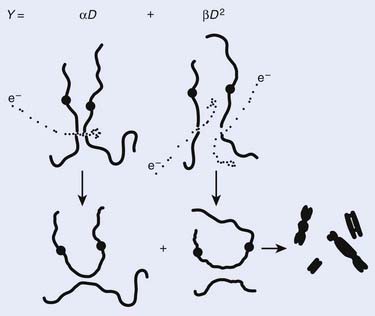
Most chromosomal aberrations are exchange types requiring two chromosome breaks for their formation, with one event or electron track producing one break and another independent event or second electron track producing the other, or in some proportion of the cases, with one electron track producing both breaks (Fig. 1-3). When two independent events must occur in close proximity in space and time, the frequency of such double events increases as the square of the total number of separate single events. This is analogous to second order or bimolecular reaction kinetics in chemistry. The single break events are, of course, directly proportional to the radiation dose, so the exchanges from a coincidence of independent events will increase as the square of the dose. Although when two breaks occur close enough together to form an exchange, they do not necessarily do so. Instead, they can restitute by joining the way they were, or they may fail to rejoin, which would result in a terminal deletion. In fact, exchange-type aberrations are much more frequent than terminal deletions in human cells. The most interesting events are those that result from the closely spaced breaks that mis-rejoin to form either a symmetrical (nonlethal) or an asymmetrical (usually lethal) exchange. When an exchange occurs between two chromosomes, the exchange is symmetrical if the exchange does not join the two centromeres together and is asymmetrical if the two centromeres are joined together. Thus, the initial break-pair forms what may be termed a potentially lethal break-pair or simply a potentially lethal lesion. This will be discussed in more detail in connection with a certain kind of repair process. As mentioned earlier, the yield of these independently produced lethal aberrations per cell, Y₂, increases as the square of the dose D, or

FIGURE 1-3 • The α/β description of chromosome aberration production Y = αD + βD² where Y is the average chromosome aberration yield per cell and D is the dose. The single-track α component of chromosome-type asymmetric interchange production (dicentrics) is shown on the left, where a single electron track produces a break-pair in each of two different chromosomes and (in some proportion of the cases) these subsequently rejoin asymmetrically to produce a dicentric and acentric fragment. The same general type of exchange process occurring in the same chromosome can produce asymmetrical chromosome-type intrachanges yielding interstitial deletions. These types of exchanges can also occur as a result of two independent electron tracks, as shown on the right. After high doses, for which the two-hit β component predominates, most of the aberrations seen in the first mitosis after G0/G1 irradiation are of these types. After low doses or dose rates for which the one-hit α component predominates, there is an increase in the proportion of aberrations that are terminal deletions, in which breaks simply fail to rejoin. In human cells, however, very few terminal deletions are observed compared to exchange types, even after low doses of IR.

where β is the proportionality constant relating to the fraction of potentially lethal break-pairs that are actually converted to lethal aberrations under a given condition. It is also possible, however, that two breaks could be produced along a single electron track. For example perhaps this would be more likely near the end of an electron track where the number of ionizations per unit track length (LET) increases.¹ In any case, the yield of such two-break single-track events would simply increase in direct proportion to dose D, rather than as the square of the dose so the yield Y₁, would be

(5)

The total aberration yield per cell Y is of course only an average; it does not mean that every cell has exactly Y aberrations. But if aberration induction occurs independently in cells and all cells have the same sensitivity, the probability that a cell will have exactly n = 0, 1, 2, 3, etc. lethal events can be calculated, because such processes are well described by the Poisson distribution that states that

(6)

and since for large numbers of cells or trials, P₀ → S (the fraction surviving), and Y = αD+βD², we can write 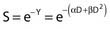which is equation (4) displayed earlier and plotted in Fig. 1-2B. Curves of the form shown in Fig. 1-2B fit experimental data very well, especially over the first and second decades of survival, but it is also the case that the curve slope continues to increase for higher doses so the curve fit is not always good in the higher dose region. This is an issue in situations where it may be desirable to estimate cell survival for high dose single fraction radiotherapy, but we will return to this later. In addition, recent studies have shown that a substantial fraction of aberrations for doses above 3 to 4 Gy, are complex, meaning they involve 3 or more breaks in 2 or more chromosomes.^50–53 The ways in which these form, and the impact on the mathematical description of dose responses from a mechanistic standpoint are not presently known, but there is still no doubt that the increase in lethal asymmetrical exchange aberrations closely follows a linear-quadratic function of dose. It has been argued that one flaw of this linear-quadratic model is that it gives a survival curve that continuously bends downward at higher and higher doses, whereas, very good experimental data for cell survival over 5 or more decades of cell killing tend to show a straight line on a log linear plot for the whole range of survivals below about 0.1. In fact, this is not a very good argument against the connection between aberrations and cell killing, because these lethal aberrations do not actually increase as αD+βD² at doses much higher than about 8 to 10 Gy; that is, they tend to saturate and approach linearity at high doses (at least up to 15 to 20 Gy).

The earlier arguments for model descriptions that best serve the purposes described have been well recognized and addressed over the past decade or so. These have been well described by several authors and the interested reader may find the descriptions and discussions of Dale,⁵⁴ Carlone and colleagues,⁵⁵ Guerrero and Li,⁵⁶ and Sachs and colleagues⁵⁷ are of particular interest. For most purposes, the α/β description is probably the best basic starting model to use, but because many workers still use the N – D₀ description, we have included it in this chapter as well.

Cellular Processing of Radiation Damage

Cells are able to process radiation damage and are largely able to repair the molecular lesions that can lead to chromosomal aberrations and cell death. In some instances, however, the repair may be incomplete, or misrepair may occur. As we mentioned previously, most lethal chromosome aberrations are exchanges (in human and other types of cells, mostly asymmetric intrachanges yielding interstitial deletions or interchanges yielding dicentrics with an acentric fragment). Two events must occur close together for such exchanges to occur, not only in space but also in time. Cells are able to repair or rejoin chromosome breaks, so if the entire radiation dose is delivered over a period of a few seconds or minutes, all the breaks that are ever going to be produced will occur together, or for practical purposes, nearly simultaneously. After such a dose given in a short period (acute dose), there would be a certain number of break-pairs, each produced by two independent electron tracks spaced close enough together for a possible exchange. However, if the same total dose were delivered over a period of several days, for example at a low dose rate, then fewer of these independent two-track break-pairs that could form potential exchanges will occur simultaneously. Even though breaks may occur in the same proximity in the cell nucleus, the break-pairs would never (or rarely) exist together, because the first break would have rejoined and disappeared long before the second break of the pair needed for an exchange ever arrived. Thus, the βD² component is very dose rate–dependent. There would, of course, still be the same number of break-pairs produced by the single-track mechanism; therefore, this αD component of cell killing is dose rate–independent and also important for mediating biologic effects of very low acute doses since the higher LET-like track ends of recoil electrons may well produce most of the lethal damage.¹ These concepts are illustrated again by reference to Fig. 1-3. Note that the formation of complex aberrations, which involve ≥3 breaks on two or more chromosomes, requires some refinement of the mechanistic description, but this does not alter the established fact that aberrations for the most part underlie cell killing in fibroblasts and epithelial cells, and at least up to doses of 8 to 10 Gy, these increase as a linear-quadratic function of X-ray or gamma ray dose.

Local chromatin topography (compaction status, epigenetic and histone modifications, accessory proteins, etc.) plays a major role in the accessibility of various repair proteins to DSBs and therefore modulates aberration induction. Evidence for this comes from the observation that both IR and restriction endonuclease-induced DSBs occur preferentially in G-light chromosome bands, i.e., euchromatic, more open regions of active gene transcription.^58–64 Similarly, a study by Barrios and coworkers who examined cells from radiotherapy patients found that the preponderance of exchange points of radiation induced interchanges occurred in G-light bands.⁶⁵ It is known that the heterochromatic inactive supernumerary X chromosomes of individuals with Kleinfelter syndrome are resistant to IR-induced chromosome interchange formation.^66,67 Recently, a study by Cowell et al. demonstrated γ-H2AX foci generated at sites of IR-induced DSBs form preferentially in euchromatic regions of the interphase nucleus.⁶⁸ The next topics for discussion are the well-studied cellular repair process known as sublethal damage repair (SLDR) and potentially lethal damage repair (PLDR). These are terms that are operationally defined.

Sublethal Damage Repair

In 1957, Jacobson presented some of the first evidence that X-irradiated cells (chlamydomonas) sustain sublethal damage (SLD) that can be repaired.⁶⁹ Jacobson showed that a radiation dose delivered in two separate fractions separated in time gave a higher survival than if the dose was given in one single fraction. The first such study of the survival of mammalian cells by Elkind and Sutton (1959) compared single-fraction acute dose radiation survival of V79 Chinese hamster cells to that following doses split into two separate fractions and delivery times.⁷⁰ In 1960, Elkind and Sutton⁷¹ extended these observations and reasoned that the shoulder on survival curves for mammalian cells (or any other cells with similar survival curves having shoulders) by itself indicates that a damage accumulation process must be involved in cell killing.²⁵ Some arguments have arisen over this point because notions of repair saturation have been suggested, but even in this instance, the putative saturation will still require damage accumulation. It also follows from this argument that cells surviving a radiation dose high enough that the survival would be off the shoulder (survival <0.1) must be sublethally damaged. In other words, cells have accumulated damage that makes them more susceptible to killing by the next IR dose than if they had not received any radiation. For this reason, such damage was termed sublethal damage or SLD.^25,71 The question they then asked was, if a population of sublethally damaged cells surviving one dose were allowed to incubate for various periods, would the cells be able to repair this sublethal damage? If repair of all the sublethal damage occurred, a dose–survival curve determined for these surviving cells should have a shoulder similar to cells that had never been irradiated. If no repair occurred, the dose–survival response should be a simple exponential decrease continuing at the survival level corresponding to the initial dose and along the same curve as for the original cell population.

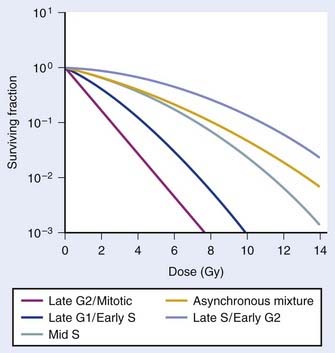
As illustrated in Fig. 1-4A, the shoulder of the survival curve indeed returned, indicating that the cells had recovered from their sublethal injury and implying that the sublethal damage had been literally repaired, so the cells were in this respect “restored to their original condition.” In further studies, Elkind and coworkers found that this shoulder returned with the half time for SLDR being of the order of half an hour.²⁵ However, as discussed in the next section on cell cycle effects, a complete return of the shoulder does not necessarily mean that all sublethal damage has been repaired. Many other workers have obtained similar results both for cells in vitro and in vivo, and repair half times range from about 0.5 to 1.5 hours. Typically, the way such studies are carried out is by the split dose technique, in which changes in survival are measured as a function of incubation time between two equal doses. The technique is illustrated in Fig. 1-4B. Generally, for an in vitro experiment, a number of identical cultures would be set up, all of which have the same number of cells that receive the same total dose, 2D; the only difference is that for some cultures, the dose would be given all at once, although for others, the dose would be given in two fractions of D, separated by various periods of time between the doses.

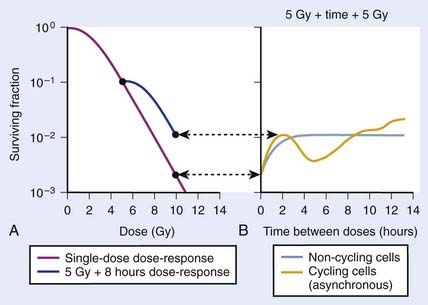
FIGURE 1-4 • Illustration of sublethal damage (SLD) and its repair (SLDR) (A), and the rate of SLDR (B). A, A single-dose dose–response curve (lower curve) and another curve obtained by first delivering a dose of 5 Gy and then incubating the cells (in this case 8 hours) before determining survival for irradiated cells that survived the first dose. If these cells returned to their initial preirradiation state, they should respond (as they do) along the upper curve from 5 to 10 Gy, whereas, if no change occurred during incubation in the cells surviving the first dose (i.e., no recovery from sublethal damage), the response would continue along the lower curve from 5 to 10 Gy. The increase in survival after the total dose of 10 Gy compared to the two 5 Gy radiation doses amounts to a factor of ∼5 in this case. B, The rate at which this increase in survival occurs shown as a function of time between the two IR doses. The complex curve for cycling cells results from the fact that there is a large difference in the radiosensitivity of cells depending on their position in the cell cycle (see text and Fig. 1-5). For noncycling cells, this cell cycle–related complexity is not observed.

The concept of sublethal damage and SLDR is readily apparent in the induction of fragment-producing exchange-type aberrations. One break by a single electron track is sublethal; by itself it almost always rejoins and is not lethal. After a certain dose, at which the survival is less than about 0.1, surviving cells will have many such single (sublethal) breaks and will, therefore, be more susceptible to killing by a further dose than if they had no previous irradiation. With incubation before a second dose, these sublethal single breaks will gradually disappear, and if the second dose is given much later, the survival of the cells will be much the same as if the cells had never been irradiated. Sublethal damage, then is damage which exists in surviving cells, by itself is not lethal, and is evident in the way it influences the response of cells to a second radiation dose. The repair of sublethal lesions is responsible for the dose-rate and dose-fractionation effects that are so important as a fundamental process in radiotherapy.

According to this view, two breaks produced by a single electron track can also lead to a lethal exchange, and the number of such events is strictly proportional to the total dose; that is, it is dose rate–independent. The contribution of this single-event two-break process to the total lethal damage is given by the αD term of equation 5. It is only the βD² term that governs dose-rate or dose-fractionation effects related to SLDR. In the simple case of the split dose experiment described earlier, if the total dose 2D is given all at once, the lethal aberration yield will be:

(7)

If the total dose 2D is given as two doses of D separated by a time sufficient to allow complete repair of sublethal damage, the yield of lethal aberrations will be:

(8)

Notice that the αD terms in equations 7 and 8 are the same, but the βD² terms differ by a factor of 2, which translates to a survival for the split dose treatment (using equations 6, 7, and 8) that is higher by a factor of 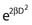than for the single 2D dose. For many small doses, or in the limit of continuous irradiation at a sufficiently low dose rate, the βD² term disappears altogether, and the only remaining damage is that from the αD component. By the same arguments, a dose-rate reduction factor depending on the rate of rejoining of breaks and their rate of formation can be applied to the βD² or repairable component of damage. This was first done by Lea⁷² for the yield of chromosomal aberrations for doses delivered over different periods of time, and by Kellerer and Rossi⁷³ in their theory of dual radiation action. Variations on this same theme^54,74,75 as well as other approaches⁷⁶ also have been described. As mentioned earlier, the recent work of Guerrero and Li⁵⁶; of Carlone et al.⁵⁵; and of Sachs et al.⁵⁷ are particularly pertinent. The general case for different dose rates derived by Dale⁵⁴ is:

(9)

(10)

There has been a great deal of discussion in recent years about the relative radiosensitivity and repair capacities of cells whose damage leads to early versus late effects in normal tissues, or effects in tumor versus late normal tissue damage. This discussion generally has been placed in the context of the α/β cell survival expression.⁷⁷ The point in question is how the responses of these tissues change with dose fractionation and dose rate. Generally, there appears to be a greater dose fractionation sparing effect with late-responding normal tissues than with early-responding tissues. In terms of α, β, and SLDR we have discussed, the radiosensitivity of the cells whose damage underlies late effects has a larger β component relative to the α component than the radiosensitivity of tumor cells or cells for early effects. Put in another way, the α/β ratio is smaller for late effects than for early effects. The α/β ratio gives an index of the proportion of damage subject to the dose fractionation sparing effect. If α were zero, the ratio would be zero, and all the damage would be reparable; therefore, for low enough dose rates or a sufficiently low dose per fraction, the killing effect of radiation would disappear altogether. As β approaches zero, the ratio increases without bound, so no dose rate or fractionation effect at all would be seen; in fact, the survival curve would be linear without a shoulder and would be described by the α component only. Furthermore, as illustrated in Fig. 1-2B, the α/β ratio corresponds to the dose for which there is an equal contribution to the damage from both the α and β components. Thus, when

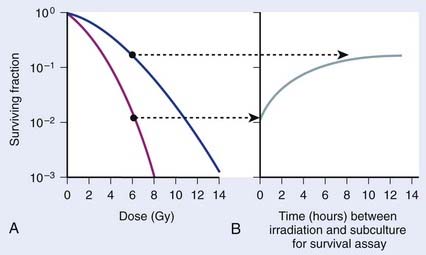
The relationship between survival and dose (using values of α and β in equation 4) has been used to convert one fractionation scheme to another fractionation scheme that is calculated to give the same amount of radiation damage as the original scheme.⁷⁸ For example, n₁ fractions of dose d₁/fraction can be converted into n₂ fractions of dose d₂/fraction with the following equation:

(11)

Variation in Radiosensitivity Through the Cell Cycle

So far we have only briefly mentioned an important factor complicating the interpretation of dose fractionation and dose-rate effects, namely the observation that the radiosensitivity of cells changes through the cell cycle. This phenomenon was first discovered by Terasima and Tolmach⁷⁹ and has been studied extensively by many others.^12,80–84 Fig. 1-5 shows dose–survival curves for synchronous cells irradiated at different stages of the cell cycle. Generally, cells in late G2 and mitosis are most sensitive, cells in mid-to-late S phase (the portion of the cell cycle when DNA is replicated) and early G2 are most resistant. Often, cells around the G1/S border (late G1/early S) are sensitive, and cells in mid-G1 are more resistant. The effect of this differential cell cycle radiosensitivity when asynchronous, randomly dividing cell populations are studied in dose fractionation experiments is that the first dose selectively kills the more radiosensitive G1 and G2 cells in the population. The surviving S phase cells continue to repair sublethal damage and begin to progress towards the more sensitive G2 and G1 phases in the cell cycle, following release from a dose-dependent S-phase delay. Both phenomena affect the way in which these cells will respond to the second dose. For example, after the first dose, the selective survival of the more radioresistant S phase cells, reflected by a large shoulder on the survival curve, complicates the interpretation of whether or not recovery of sublethal damage is complete. For complete recovery, the shoulder of the survival curve for the second dose should be larger than the shoulder for the first dose delivered to the original asynchronous cells (consisting of both radiosensitive G1 and G2 phase cells and radioresistant S phase cells).⁸⁵ Because the rate of SLDR is usually faster than cell cycle progression, SLDR leads to the rapid early increase in survival in split-dose experiments. By contrast, cell cycle progression leads to a gradual decrease in survival over time (via cell cycle redistribution or reassortment), but is eventually followed by an increase in survival as the semisynchronous surviving population divides (repopulates) (see Fig. 1-4B). These three processes have been referred to by Withers as three of his four R’s of radiotherapy, that is, repair, redistribution, and repopulation (along with the fourth R, reoxygenation, discussed later).⁸⁶

FIGURE 1-5 • The cell cycle dependence of radiosensitivity. The figure shows typical survival curves for cells irradiated in various phases of the cell cycle. Also shown is the survival curve for an asynchronously dividing log phase culture, which is composed of a mixture of cells with their sensitivities indicated. In this case, the curve labeled asynchronous mixture is a composite curve for a cell population consisting of 15% of cells in late-G1/early-S, 50% in mid-S, 25% in late-S/early-G2, and 10% of cells in late-G2/M. This curve for asynchronous cells looks fairly homogeneous, and it would be difficult to deduce from a simple inspection of the curve that, in fact, it is derived from a cell population composed of subpopulations with very different radiosensitivities.

Cell cycle dependent radiosensitivity and progression of cells in the cycle after irradiation can be important factors, both in comparing the radiosensitivities of different cell types and in determining the responses of cell populations in normal tissues and tumors when doses are fractionated or delivered continuously at low dose rates.^{38,81,87–89} For example, accumulation of cells in the radiosensitive phase at the end of G2 can, in certain instances, overshadow the dose-rate effect due to repair, such that the effect per unit dose actually increases rather than decreases with a reduction in dose rate.⁸⁸ In general, irradiated cells have the greatest cell cycle delay during G2, with approximately 1 to 2 min per cGy for cells irradiated in late S and G2²⁵ and about one third less delay during G2 when they are irradiated in G1 or early S.⁹⁰ The delay from G1 into S is usually only an hour or two, even for doses as high as 6 Gy,⁹⁰ but appears to increase in cells that express wild-type Tp⁵³ (discussed later).⁹¹ The accumulation of cells in G1 that is observed approximately 16 hours after irradiation in cells expressing wild-type Tp⁵³ is also associated with accumulation of cells in G2,⁹² and this reduction in the number of cells in the radioresistant S phase should cause a reduction in the shoulder of the survival curve for a second dose delivered ∼16 hr after the first dose (see Fig. 1-4). A simple illustration of effects of heterogeneous populations on radiation survival curves, with explanatory equations, was presented many years ago,⁹³ and has been discussed and applied in practice on other occasions.^25,94

Finally, it is extremely important to consider the overall distribution of cells in the cell cycle when comparing the radiosensitivities of different cell lines and other IR-related biologic endpoints. For example, if two cell lines, line A and B, had identical radiosensitivities, but the line A culture was primarily distributed in G1 at the time of irradiation, while the line B culture had its cells primarily distributed in S or was dividing asynchronously, a comparison of the radiation responses of cell lines A and B would lead to the erroneous conclusion that line A is more radiosensitive than line B (compare G1 with asynchronous or S cells in Fig. 1-5). This important concept of intrinsic cellular and differential cell cycle-phase radiosensitivity prompted Steel, McMillan, and Peacock⁹⁵ to suggest a fifth “R” for radiation therapy, in addition to Wither’s original 4 R’s.⁸⁶

Potentially Lethal Damage Repair

Cell survival also can be altered by the incubation conditions of cultures after irradiation. Many years before the work with mammalian cells, experiments showed that holding bacteria for a time after irradiation in a buffered salts solution and then plating for the survival assay gave a much higher survival than if the cells were kept in full nutrient broth after irradiation.⁹⁶ This phenomenon is referred to as liquid holding recovery. Similarly, if mammalian cells are held in suboptimal growth conditions for various times after irradiation, such as by treating cells with metabolic inhibitors,⁹⁷ balanced salts solution,^25,98 reduced temperatures,^44,99 or maintaining cultures in G0/G1 contact inhibition^48,100 or under serum starvation,¹⁰¹ their survival is greatly enhanced. This is illustrated in Fig. 1-6 for holding cultures in plateau phase.¹⁰²

FIGURE 1-6 • A, The effect of potentially lethal damage (PLD) and its repair (PLDR) on the dose–survival responses of cells for immediate versus delayed subculture. B, Survival increase due to PLDR after 6 Gy as a function of time of delay of subculture. PLD is operationally different from SLD. PLD is damage that is either expressed or repaired depending on postirradiation conditions. Cells that may survive for a dose given under one condition but may not survive the same dose under another condition. In contrast to SLDR, the increase in survival resulting from PLDR is not caused by a change in the response of cells surviving one dose before a second dose, but, in this particular example, but rather it shifts the balance between damage repair and misrepair or fixation in favor of increased repair when cells are kept in density-inhibited plateau phase (delayed subculture) rather than being immediately subcultured after irradiation.

In Fig. 1-6A, survival curves are shown for apparently normal primary human fibroblasts irradiated as plateau-phase G0/G1 cultures and then either subcultured immediately or 24 hours later to assess survival by single-cell colony formation. In Fig. 1-6B, the rate of PLDR is reflected by an increase in survival as a function of the time delay between irradiation and subculture for the survival assay for cultures receiving the same dose. The interpretation of such observations was that radiation produced lesions that were potentially lethal, and that under one set of incubation conditions, a damage repair process operating in opposition to a damage fixation process resulted in a certain fraction of these lesions being converted to nonlethal lesions (via repair and restitution) while the remaining fraction was fixed into lethal lesions that killed the cells (via an improper misrepair event or a lack or repair).¹⁰³ As postirradiation conditions are changed, they may become more favorable to the repair processes, less favorable to the fixation processes, or both, so that the final result would be a higher proportion of the potentially lethal lesions being converted into nonlethal lesions. From the perspective of chromosomal aberration formation, a highly quantitative correlation between cell survival and the yield of aberrations is observed following manipulation of postirradiation culture conditions.⁴⁸ One set of incubation conditions may favor the restitution of breaks as opposed to exchange, while for another set, restitution is less favored.^44,104 The reason for this phenomenon is not known, although we know that certain suboptimal growth conditions, such as holding cultures in plateau-phase confluency, favor restitution. Also, treatment with anisotonic salts, which inhibits PLDR and SLDR,^105,106 greatly affects chromatin structure, which could alter the proximity of lesions, such as DSBs and clustered DNA damage lesions,¹⁰⁷ in some way to affect the fixation and repair processes involved in aberration formation.^104,108,109

Numerous reports of postirradiation colony formation ability, mitotic and PCC-induced chromosomal aberration induction, gel electrophoresis and γ-H2AX foci kinetics over the last 40 years have documented similar kinetics of PLD repair,^{48,85,100,110–117} with the majority (≥90%) of PLD repaired by 6 hours. Repair of PLD has been noted in most cell lines examined (except ATM^−/− and BRCA1^−/− cells), both normal and malignant in origin, making clinical use of chemical inhibitors of PLD processes ineffective for cancer treatment purposes.^118–120 Weichselbaum et al. proposed a link between intrinsic PLD repair capability and the radiocurability of tumors,¹²¹ but further work¹¹⁹ could not substantiate such a correlation. Although the degree of cellular PLD response may be of little prognostic value in the radiotherapy clinic, such variations may be of great importance for the study of the responsible molecular repair mechanisms. For example, Schwartz et al.,¹²² Franken et al.,¹²³ and Alsbeih et al.¹²⁴ recently showed PLD repair to be a Tp53-dependent process. Functional inactivation of Tp53 by HPV-16 infection or direct mutation of Tp53 in human and isogenic mouse cell lines significantly moderated the increases in survival following 24 hours of confluent holding. However, since Tp53 gene inactivation is a classic feature of transformed and tumor cells, the observation that many tumor cells demonstrate PLD repair indicates other (Tp53-independent) pathways in these cells must also contribute to this response.

Chemical Modification of Radiation Damage

Details on modification of radiation damage by chemical sensitizers such as oxygen or other electron-affinic agents or chemical protectors such as sulfhydryl amines or thiophosphates are provided elsewhere in this volume, but it is appropriate to mention briefly the way such agents act to modify the parameters of dose–response relationships discussed earlier in this chapter. Most of these agents act as dose-modifying agents and alter the dose response curve by a parameter termed the dose modification factor (DMF). This is called a synergistic type of interaction between the modifying agent and IR, which is distinctly different from an additive type of interaction that only reduces the shoulder of the survival curve. For an independent type of interaction, the overall shape of the IR survival curve is unaffected, but is shifted downward by an amount equal to the reduction in survival (the DMF) resulting from treatment with the modifying agent.¹²⁵ In fact for these types of independent interactions, following treatment of synchronous populations or asynchronous populations with minimal variation is modifying agent-induced cytotoxicity through the cell cycle, the net survival for the combination of both agents is simply the IR survival multiplied by survival for the dose of modifying agent employed (see Dewey et al.,¹² and Dewey¹²⁵ for these definitions and discussion of complications caused by cell cycle variations in sensitivities to the two agents).

Oxygen is the classical example of a synergistic type of interaction with IR. Oxygen sensitizes cells to IR by reacting directly with damaged target radicals to fix them or render them less capable of repair by a competing, fast hydrogen-donating reaction, which restores the damaged target molecules to their original condition. Other cellular species, such as reactive nitrogen species (RNS), can also act in a way similar to oxygen by causing damage fixation (not repair). When the concentration of oxygen is reduced, for example to only about 1% to 2% of the concentration of O₂ in air (159 mm Hg), fewer oxidative radicals are present to fix the damage, so increased fast repair by hydrogen donation occurs. Oxygen, therefore, simply increases the yield of fixed target radical species, producing essentially the same effects observed by increasing the low LET radiation dose without the presence of oxygen. This oxygen effect disappears with increasing LET, and oxygen must be present during irradiation or within a few milliseconds after irradiation to produce radiosensitization. The role played by oxygen in metabolic respiratory processes has nothing to do with its radiosensitizing effect. The oxygen effect is the same whether the irradiation occurs at 37° C or at 0° C, at which point oxygen-dependent cellular respiration is greatly slowed.

When a sensitizing agent like oxygen acts as a simple dose modifying agent—in this case, the DMF is ∼3.0 for fully oxygenated versus anoxic conditions (this is the maximum oxygen enhancement ratio or OER)—then, only about one third the IR dose or D/3 is required to produce the same level of effect produced by the dose D in the absence of oxygen. The effect on the mathematical dose–response relationship and survival curve is then easy to calculate, as shown below. For the N – D₀ expression, if the survival under anoxic conditions S_N is

As can be seen by multiplying both the numerator and denominator of the exponent by 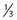, so that

the oxygen effect effectively reduces the D₀ by a factor of 3 without changing the extrapolation number N. A similar calculation applies for the N, D₁, D_n–based expression in equation (3).

For the α/β survival expression, if the survival under anoxic conditions S_N is

Oxygen in this case has the effect of increasing the anoxic α constant by a factor of three and the anoxic β constant by a factor of 9.

This threefold increase in dose required for a given amount of IR-induced cell killing under hypoxic conditions compared with irradiation under oxygenated conditions is thought to play an important role in radiotherapy.^126–128 Many tumors contain a significant fraction of hypoxic and therefore radioresistant cells compared to the well-oxygenated cells in surrounding normal tissue. For a single acute dose of IR, the dose required to kill about 90% of the tumor cells (e.g., a survival fraction of 10⁻¹³ for a tumor with 10¹² clonogenic tumor cells) would have to be about three times larger than it would be if all of the cells in the tumor were well oxygenated. However, the situation is not this bleak, because in most tumors, considerable reoxygenation occurs during fractionated radiotherapy. This reoxygenation effect is Wither’s fourth “R” of radiotherapy, which follows the three “R’s” mentioned previously, i.e., repair, redistribution, and repopulation.⁸⁶ It should also be noted that not all tumor cells are likely to be equally clonogenic and capable of regenerating a tumor (often referred to as tumor or cancer stem cells); this will lower the total number of cells in a tumor that require inactivation.^129,130

Similar calculations can be made for radioprotective compounds that act as dose modifying agents, except that to calculate the biological effect in the presence of the protector, IR doses delivered in the absence of the protector must be divided by the DMF. Cysteine has been shown to act as a dose modifying radioprotector with a DMF of about 1.5 to 2, which results in an effective reduction of α by 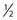and β by 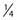.^131,132

Radiation Quality, Relative Biologic Effectiveness, and Linear Energy Transfer

Radiation quality has been known for a long time to affect biologic responses to ionizing radiation. Densely ionizing radiations such as alpha particles and heavy charged particles (HCP) are more effective in killing mammalian cells than sparsely ionizing X-rays or gamma rays. The relative biologic effectiveness (RBE) of radiations with different qualities (i.e., different linear energy transfer or LET values) is defined as the ratio of doses of two different types of radiation that are required to produce the same degree of the same biologic effect. X-rays generated at 250 kV_p have been widely used in radiobiologic studies, so they became the standard used for RBE comparisons and calculations. The RBE of a test radiation in question is then defined as:

Naturally, other irradiation conditions such as oxygenation levels, dose-rate, and so on, should be equal.

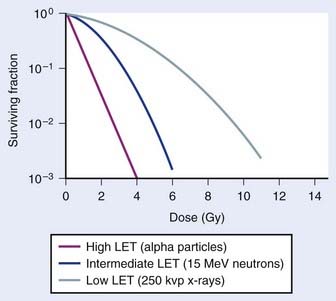
An example of the dose–survival curves for mammalian cells for radiations of different LET is shown in Fig. 1-7. The LET is, to a first approximation, a track-averaged description of the density of ionizations along the ionization track in irradiated material and increases as the LET increases. Actually, more sophisticated microdosimetric and nanodosimetric quantities (such as lineal energy) are used for precisely describing radiation quality, but for our purposes, LET is a sufficient tool. Low-LET ionizing radiations such as β particles and secondary electron recoils from X-rays and γ-rays deposit energy stochastically in materials by liberating secondary electrons with tortuous track structures and have LET values on the order of 0.3 to 1 keV/µm (β particles are primary electrons released from radioactive decay processes of unstable radioactive nuclei). High-LET ionizing radiations such as alpha particles, nuclear fragment recoils from high-energy neutron interactions, and other HCP such as constituents of galactic cosmic radiation (GCR) deposit their energy along more direct tracks producing nuclear (i.e., atomic) fragments and scattering secondary high-energy delta-ray electrons with combined LET values that may approach 1000 keV/µm or more.¹ It should be noted that protons used in radiotherapy have an LET of ∼1.0 keV/µm, similar to x-rays and gamma rays.^133,134 Protons have the primary advantage of improved dose distribution compared to photon and electron beams, however the risks of low dose scattered neutron exposures in the surrounding normal tissues remains to be determined and addressed.¹³⁵

FIGURE 1-7 • Dose–response curves for radiations with different linear energy transfer (LET) values. The relative biologic effectiveness (RBE) of neutrons or alpha particles relative to the x-rays is defined as a ratio of doses required to produce the same level of biological effect, with the numerator of the ratio being the x-ray dose and the denominator being the dose of the other radiation type being compared.

The relationship between RBE and LET can be illustrated in terms of cell killing caused by the induction of chromosomal aberrations. For low LET x-rays or gamma rays, the distance between ionizations or ion clusters along an individual recoil electron track is almost always greater than the minimum interaction distance for two chromosome breaks to interact to form an exchange (∼0.2 to 0.5 µm^136,137). Therefore, two or more electron tracks are usually necessary to form an exchange, and most of the ionizations that contribute to the total dose are “wasted” because they are unlikely ever to be involved in generating a potential aberration-producing break-pair. As the LET increases, a peak in RBE is eventually reached at which an optimum spacing of ionizations occurs for producing break-pairs with maximum efficiency.¹ This optimum RBE also probably includes a repair component, since the higher density of damage also appears to influence the processing and repair of DNA damage and also the complexity of IR-induced chromosomal aberrations.^{107,138–140}

Related posts:

Plasma Cell Tumors Cancer of the Stomach Cancer of the Thyroid Cancer of the Uterine Cervix Cancer of the Vagina Cancer of the Vulva

Stay updated, free articles. Join our Telegram channel

Join