69 Proton Therapy

Radhe Mohan, PhD, Michael T. Gillin, PhD, Shiao Y. Woo, MD, FACR, Andrew K. Lee, MD, MPH

Rapidly increasing interest in proton therapy is evident in the large attendance at proton therapy meetings and symposia, the growth of proton therapy vendors, and the growing involvement of major radiotherapy equipment manufacturers. At the time of writing (November 2009), there were seven hospital-based proton therapy centers operating in the United States (source http://ptcog.web.psi.ch). Many more are being built and planned around the world. In addition, at least two companies have entered the business of making small, single-room proton therapy facilities using compact accelerators.

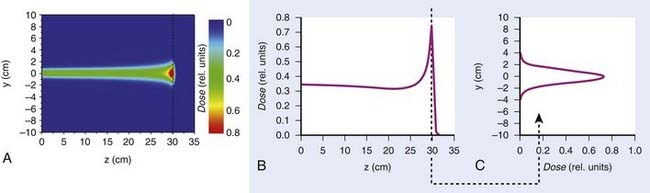
Such interest in protons (and, more generally, in heavier charged particles) is sparked by their energy deposition characteristics. Protons continuously interact as they traverse through a medium, losing energy along the way until they come to a stop. They deposit the greatest amount of energy per unit path-length near the end of their range. A characteristic depth–dose curve and beam profiles for a narrow monoenergetic beam of protons are shown in Fig. 69-1A. The peak of highest dose is called the Bragg peak. Dose distribution from such a beam would be of limited use in treating cancers of arbitrary shape and size. A therapeutically useful beam can be produced in two ways: (1) by appropriately modulating the energy of the initially narrow monoenergetic beam as well as scattering it laterally to cover a target volume of a given size, or (2) by scanning the narrow (pencil) beams of a sequence of energies magnetically. The former modality is called passively scattered proton therapy (PSPT). Fig. 69-2 shows a typical PSPT dose distribution in water, a distribution characterized by a lower dose at the entrance, a flat region called the spread-out Bragg peak (SOBP), and rapid fall-off at the distal edge. This figure also illustrates how a sequence of Bragg peaks of appropriate intensities adds to produce the SOBP. Such a dose distribution requires further custom shaping with a block or an aperture to conform the lateral dimensions of the beam to the shape of the target and a range compensator to conform the distal edge of the dose distribution to the distal edge of the target volume. In proton therapy with scanning beams, the intensities of thin proton “pencils” of a range of energies, terminating at a matrix of points in the target, are determined using optimization techniques to achieve specified clinical objectives. This is the proton therapy equivalent of intensity-modulated photon (radiation) therapy (IMRT, also called IMXT or intensity-modulated x-ray therapy) and is called intensity-modulated proton therapy (IMPT). Regardless of the modality, generally two or more fields are used per treatment fraction, though the number of fields for proton therapy is usually smaller than the number for photon therapy.

FIGURE 69-1 • Pristine Bragg peak (A), depth dose (B), and profile (C) of a narrow, monoenergetic 219.3-MeV proton beam. The profile corresponds to the depth of maximum dose.

FIGURE 69-2 • Spread-out Bragg peak in water (A) and cross-beam profile (B) in air of a modulated beam of protons of an initial energy of 250 MeV, scattered to a diameter of 25.5 cm and blocked to a 10 cm × 10 cm square field.

The characteristics of protons described in the previous paragraph, namely lower entrance dose and no dose beyond their range, lend themselves to a greater ability to confine regions of high therapeutic doses to the target volumes to a much greater degree than photons. A consequence of this is greater sparing of normal tissues as well as considerable reduction in integral doses for the same target dose. This has clinical implications when adjacent normal tissue may be highly sensitive to even low radiation doses (e.g., lung parenchyma) and/or when the lower doses to adjacent tissues allow dose escalation to the target. Protons have been shown to be an effective modality for the treatment of several types of cancers. Examples include uveal melanomas, chordomas and chondrosarcomas of the base of skull and axial spine, small lung and liver tumors, paranasal sinus cancers, and solid pediatric tumors. However, it is important to note that protons are more vulnerable to uncertainties such as those due to respiratory motion and day-to-day anatomic changes. This necessitates the use of larger margins. Substantial current research is directed at minimizing uncertainties and their consequences and to further improve of protons effectiveness.

This chapter’s four remaining sections describe and discuss the basic physics of proton therapy, the clinical issues relevant to proton therapy, our clinical experience with proton therapy of head and neck (HN), pediatric, and central nervous system (CNS) cancers, and the same for thoracic, abdominal, and pelvic cancers.

General Principles of Physics of Proton Therapy

Although, in the routine practice of proton therapy, one does not need to think about the principles of physics at the basic level, it is helpful to understand its fundamental processes to appreciate the potential and limitations of proton therapy, to be able to explain the observed characteristics of dose distributions, and to understand the uniqueness of the methods needed for the planning and delivery of treatments and for dosimetry.

Interactions of Protons With Matter

Proton dose distribution characteristics arise from the way protons interact with the medium they traverse. The primary interactions in order of predominance, are (1) Coulomb interactions with electrons (2) Coulomb interactions with nuclei, and (3) nuclear interactions.

Protons lose most of their energy through interactions with atomic electrons. For 200 MeV protons, for instance, the electronic stopping power in water is 4.49 MeV cm²/gm, whereas the nuclear stopping power is 1.52 × 10⁻³ MeV cm²/gm. The secondary electrons travel very short distances from the path of the proton while ionizing atoms and molecules and depositing energy. The energy deposited by a proton per unit distance traveled (dE/dx, called linear energy transfer or LET) increases inversely as the square of the velocity. Thus, in a uniform medium, monoenergetic protons will travel a well-defined distance, losing energy at an increasing rate before coming to a stop. This leads to the formation of the characteristic Bragg peak. Because the proton is much heavier than the electron, its interactions with electrons do not result in an appreciable change in its direction.

When protons pass in the proximity of nuclei, they are deflected by Coulomb repulsion but without losing a significant amount of energy. Although each deflection is small, multiple such deflections, called multiple Coulomb scattering in totality, result in significant lateral dispersion of protons and are the major contributors to the width of the beam penumbra. Furthermore, when a proton beam passes through a complex heterogeneity, consequent variations in lateral dispersion can lead to substantial dose heterogeneity. It should be mentioned that inadequate management of the lateral dispersion is one of the important weaknesses of the semiempirical methods of dose computation used in current treatment planning systems.

Protons also suffer elastic and nonelastic scattering with nuclei when they traverse media. The cross-section (i.e., the probability) of nuclear interactions is small relative to Coulomb interactions. The primary proton imparts a substantial fraction of its energy to the target nucleus during a nuclear interaction and may scatter through a large angle. In elastic nuclear scattering, the target nucleus only recoils (kinetic energy is conserved); whereas in nonelastic scattering, the target nucleus may be left in an excited state, a nucleon exchange or transfer may occur (e.g., p-n reaction), or the target nucleus may disintegrate into smaller fragments. (A special category of nonelastic scattering is the inelastic scattering in which the excited nucleus emits a γ ray and returns to its ground state.) Recoil nuclei and the heavier fragments are absorbed within very short distances from the point of interaction. However, scattered protons may travel relatively large distances and contribute to a low dose “halo” that must be explicitly taken into account for accurate computation of dose distributions.

Nuclear interactions also result in the production of neutrons, an unwanted byproduct. Neutrons can travel large distances and necessitate the use of a large amount of shielding. They may also induce a significant level of radioactivity in the metallic objects they pass through and are of major concern because of their carcinogenic potential. Experts have cautioned about neutron contaminants when using passively scattered proton beams, especially for pediatric treatments.¹^–⁴ However, the designs of newer treatment delivery systems have substantially reduced neutron contaminants in the incident passively scattered beams. Of course, neutron contamination in the incident scanned beam is essentially zero. Neutrons generated in the patient are unaffected, but their number is relatively small.

The probability of nuclear interactions rises with atomic number and with the energy of protons and, correspondingly, the magnitudes of the halo effect and neutron production. It is estimated that about 20% of protons of energies in the therapeutic range undergo nuclear interactions at some point along their path.

It is worth noting that an important difference between protons and photons is that an attenuator placed in the path of photons changes the intensity (number) of photons with only a small effect on the energy spectrum, whereas for protons, it changes its energy spectrum and has only a small effect on the number of protons.

Proton Accelerators

Protons of energies in the range of 70 to 250 MeV are needed for the treatment of cancers. For passive scattering, an initially monoenergetic beam of desired penetration is modulated to produce protons of a sequence of lower energies to form the required depth dose distribution and scattered mechanically to achieve lateral spreading. For scanning beams, the initial beam is a composite of pencil beams for the range of energies necessary that are spread magnetically to produce the desired dose distribution.

Typically, protons for therapeutic applications are accelerated using a cyclotron or a synchrotron. Both types of accelerators are used in radiation therapy, and each has its advantages and disadvantages. Cyclotrons are more compact and have higher beam intensity. They produce a continuous stream of protons. Protons are accelerated to the maximum of the energy for the specific accelerator. Clinically desired initial energies are then achieved by rapidly inserting mechanical degraders in the proton stream (beam line) before it enters the treatment room.

Synchrotrons, on the other hand, accelerate batches (pulses) of protons to the desired energy levels. Protons gain in energy with each revolution through the accelerator. As soon as a batch has reached the desired energy, it is extracted and transmitted via the beam line to the treatment room for delivery. The extraction may occur over a variable period of time (anywhere from 0.5 to 5 seconds), depending on the application. The accelerator then goes through deceleration and reset steps and starts the next cycle. Each cycle may produce protons of different energy. Generally, synchrotrons have greater energy flexibility, smaller energy spread, and lower power consumption. Because of the pulsed nature of the beam, proton scanning beams with synchrotrons is more complex than for cyclotrons.

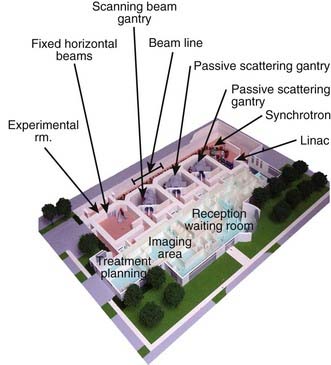
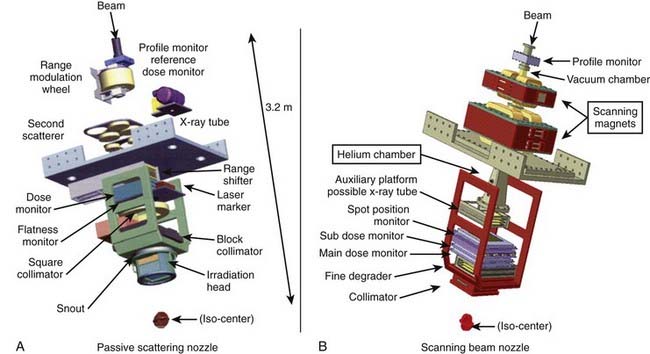
The narrow beam of protons produced by the accelerator has a relatively small initial energy and angular spread. After extraction from the accelerator, the beam is directed magnetically through the beam line to the gantry and into the treatment head or “nozzle.” The term nozzle is used in particle therapy to describe the treatment head that the beam passes through after leaving the evacuated beam line. Fig. 69-3 shows the treatment floor configuration at the M.D. Anderson Proton Center (MDACC) and Fig. 69-4 shows the schematics of the passive scattering and scanning beam nozzles of the Hitachi proton synchrotron, the accelerator at MDACC. Its important components are described in the figure caption.

FIGURE 69-3 • The schematic of the treatment floor configuration at M.D. Anderson Cancer Center proton therapy facility. The same proton accelerator serves multiple rooms through the beam line.

FIGURE 69-4 • Schematic drawing of the components of the (A) passive scattering and (B) scanning beam nozzles of the Hitachi proton therapy system in use at M.D. Anderson Cancer Center. The key components of the passive scattering nozzle are the range-modulator wheel, a second scatterer, a range shifter for fine control of the maximum range, a snout to mount the field shaping blocks and compensator, and beam monitoring devices. The most important components of the scanning beam nozzle are the x- and y-scanning magnets and monitor chambers for monitoring the profile, position and dose. Both nozzles also contain x-ray tubes that can be moved in-line for radiographic alignment of the patient.

For PSPT, protons of a small number of discrete initial energies spanning the therapeutic range are directed into the gantry. Only one of these energies is dialed in for a given beam. The beam energy may be further reduced in fine steps using thin slabs of water-equivalent material called range shifters. For scanning beam applications, energies entering the nozzle are much larger in number and at finer steps. For instance, for PSPT, the MDACC system has a set of eight initial energies from 100 MeV to 250 MeV; whereas for the scanning beam, there are 94 energies from 72 MeV to 221 MeV. Protons with these energies have maximum approximate penetration ranging from 4 cm to 30 cm, respectively.

A typical proton accelerator serves multiple rooms. In the newer designs, the beam is switched automatically from one room to the next based on the order of request and priority. At the time of this writing, single-room accelerators are being developed by at least two different commercial vendors.

Therapeutic Proton Beams

A beam of protons entering the nozzle is a focused, circularly symmetric thin pencil. As it traverses the air and monitoring devices, it spreads out slightly by the time it reaches the surface of the medium (patient, phantom, compensator, etc.). Once it enters the medium, the rate of interactions increases substantially. Typical dose distribution in water from such a beam is shown in Fig. 69-1. To be clinically useful, such distributions must be spread out laterally and longitudinally (i.e., in the direction of the beam). This can be achieved by either passively scattering protons with a combination of a rotating range modulation wheel (RMW) and a scattering foil or by varying the energy of the protons before they enter the nozzle and actively scanning with magnets.

Passively Scattered Proton Beans

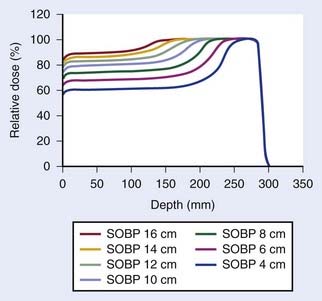
Conventionally, proton dose distributions of therapeutic interest have been produced by passive scattering. In the technique most commonly employed, an RMW is used to produce protons of a sequence of energies up to a maximum. The RMW is like a propeller that is placed in the path of protons. It has multiple banks of steps of a range of thicknesses each. Fig. 69-5 shows the design of a Hitachi RMW. It has six banks of steps and rotates at 400 revolutions per minute, thus it modulates the initial beam’s energy 40 times per second. As the wheel rotates, the proton beam passes through different thickness of the material and is slowed down to different energies. Angular widths and thicknesses of the steps are designed so that the sum of the resulting individual Bragg peaks results in a flat, homogeneous depth dose distributions of the type shown in Figs. 69-2 and 69-6 and called the SOBP. The thinnest step corresponds to the deepest penetration and the thickest one corresponds to the most proximal Bragg peak desired. SOBPs of in-between widths may be achieved by turning the incident beam off and on repeatedly at predetermined angles during the wheel’s rotation.

FIGURE 69-5 • Two views of a typical range-modulator wheel for the Hitachi proton therapy system. The wheel rotates at 400 rpm and modulates the incident beam six times per rotation, each modulation presents a series of steps to the monoenergetic proton beam producing a series of Bragg peaks. The angular width of each step is proportional to the intensity of the corresponding Bragg peak. These widths are chosen so that the sum of Bragg peaks is a spread-out Bragg peak (SOBP) of the type shown in Fig. 69-6. Turning the incident beam off and then on again on modulator steps less than the maximum thickness is used to produce SOBPs of different modulation widths. In combination with a second scatterer, the range-modulator wheel spreads the beam laterally to a size of predetermined diameter.

Designs and the number of RMWs for a treatment delivery system vary with vendors. The Hitachi system, for instance, has 24 RMWs for each room, or three sets of eight for field sizes of up to 10 cm × 10 cm, 18 cm × 18 cm, and 25 cm × 25 cm, each set of eight corresponding to a range of eight energies. The RMW for a given energy and field size is inserted manually. Field-size specific spreading of protons means fewer neutrons. In the ion beam applications (IBA) design, three RMWs are mounted on a carousel. Each RMW has three separate concentric tracks that can be positioned in the proton beam path to modulate three different initial energies. This design drastically reduces the number of RMWs and allows automated insertion of RMWs.

In the current designs, two scatterers made of high-atomic number materials are used to spread the beam laterally and make it flat within the region of interest. Often, the first scatterer is built into the RMW. The second scatterer plays the same role for protons as the flattening filter for photon beams. Its design is such that the proton energy across the flattened beam is constant, thus assuring beam flatness at depth. The design of the second scatterer depends on the required spreading (field sized) and the initial energy. Thus, multiple second scatterers are required. The Hitachi system, for instance, has nine second scatterers.

The use of scatterers and RMWs reduces the maximum range of protons. The reduction depends on the degree of spreading For instance, whereas the range of the 250 MeV unscattered beam is approximately 36.5 cm in water, it is approximately 32.5 cm when scattered to uniformly cover field sizes up to 10 cm × 10 cm, 28.5 cm to cover fields up to 18 cm × 18 cm, and 25.0 cm to cover fields up to 25 cm × 25 cm.

Scanned Beams

Magnetic scanning of thin pencil beams provides greater flexibility and control for creating optimum conformal proton dose distributions. In addition, the elimination of mechanical shaping devices (such as apertures and compensators) saves the time required for the insertion of these devices and eliminates the need to enter the treatment room between fields, thus, making treatments more efficient. Protons in a pencil beam incident on a patient or phantom are very nearly monoenergetic and are distributed essentially as a narrow Gaussian function of position relative to the pencil beam’s center. The lateral dimension of a pencil beam is expressed in terms of σ of the Gaussian or in terms of its full width at half-maximum (FWHM; 2.35 × σ). A smaller σ is desirable, because it allows for a sharper penumbra and greater control of dose distributions. In air, higher energy proton pencil beams have a smaller σ than the lower energy ones. Typically, the smallest achievable σ for the highest energies (220 to 250 MeV) ranges from 3 to 5 mm. Once the pencil beam enters a medium, such as a phantom or a patient, the σ increases substantially, especially near the end of the range of protons. This is illustrated in Fig. 69-1 for a Hitachi proton therapy system, which shows the dose distribution of a single pencil beam in water for a proton beam of range 21.5 cm (corresponding to an energy of 181.05 MeV). The FWHM of the pencil beam at the end of its range in water as a function of energy varies from approximately 12 mm for 220 MeV to 21 mm for 120 MeV.

The high dose region at the end of the range of a pencil beam is often referred to as the spot. The spot size is of special concern for scanned proton beam therapy. It affects the width of the penumbra and limits the fineness of the adjustment of the dose possible to achieve optimum IMPT dose distributions. Most recent designs of proton therapy systems are considering multileaf collimators to reduce the penumbra width; however, this is at the expense of some increase in neutron dose. It is often stressed that it is important to reduce the spot size by improving focusing and reducing the material in the path of the incident beam (e.g., replacement of air with helium or vacuum) or by reducing the drift space between the point where the protons enter the nozzle and the isocenter. However, these measures will only reduce the scattering in air and have no effect on scattering in the medium. Since the two effects combine in quadrature (i.e., as the square root of the sum of squares), the net gain is expected to be small.

The treatments with scanning beams are also referred to as spot scanning treatments. The lateral position of the spot is controlled by two orthogonal magnets, and the range of the spot is controlled by changing the energy of the incident pencil beams. The maximum depth of penetration of the pencils in tissue equivalent materials may vary from a few cm for the lowest energies to more than 36 cm for 250 MeV. Fig. 69-4B shows the Hitachi scanning beam nozzle. Field sizes of up to 30 cm × 30 cm can be achieved in this system.

Scanned beam treatments are delivered using either raster scanning or discrete spot scanning (DSS) depending on the design of the specific system. In the case of raster scanning, the pencil beam is moved continuously while its intensity is varied. In DSS, the pencil beam is stopped, a specified dose is delivered, irradiation is then turned off and the pencil beam is moved to the next spot. In either case, the dose is delivered in “layers,” one layer per energy. Upon completion of one layer, the energy is changed to the next one in sequence. The positions and intensities (in terms of monitor units) for a matrix of spots within the target volume for each scanned beam are determined by the treatment planning system to achieve acceptable or the best possible approximation of the desired dose distribution.

Proton scanning beams have been in use for patient treatments at the Paul Scherer Institute since 1996, where a one-dimensional scanning of proton pencil beams of different energies in the patient’s transverse plane is used. The other dimension is achieved by moving the couch along the patient’s longitudinal axis. Many facilities are now at various stages of implementing 2D scanning as described above. The first use of 2D scanning occurred in May, 2008 at MDACC, where it is now being used routinely. However, it is still an evolving technology with much research and development to be done.

Field Shaping

When a passively scattered beam is used to irradiate a water phantom, it produces a dose distribution with the depth dose characteristics depicted in Fig. 69-6 and an axially symmetric lateral distribution that tapers off gradually beyond the maximum radius of the intended flat region. To conform the dose distribution laterally to the shape of the target volume (plus appropriate margins), an aperture, typically made of brass of sufficient thickness (2 cm to 8 cm) to absorb incident protons of highest energy, is used (Fig. 69-7). Brass is a compromise material because it produces fewer neutrons than, say, lead or Cerrobend and yet the apertures are sufficiently compact and manageable. As illustrated in the schematic of the Hitachi passive scattering nozzle in Fig. 69-4A, the field aperture fits in a “snout,” a component at the end of the nozzle designed to hold field shaping devices. To achieve sharp beam boundaries, the field aperture is positioned close to the patient. However, the gap between the aperture and the patient reduces the intensity of the hot spots at shallow depths caused by protons scattered from the aperture. As mentioned above, the designers of the new proton therapy systems are considering multileaf collimators to shape the lateral field boundaries.

FIGURE 69-6 • Measured spread-out Bragg peaks for a series of beam widths. The proton beam is “gated on” at the thinnest part of range-modulator wheel and “gated off” when the range-modulator wheel has rotated through a certain angle to achieve the spread-out Bragg peak of desired width.

FIGURE 69-7 • A 2-cm-thick brass aperture used to shape the proton beam. Three identical pieces are required for the 250-MeV proton beam and fewer for lower energies.

To create a dose distribution that conforms to the distal shape of the target, the SOBP of the passively scattered beam is shaped further by using a range compensator. A compensator is usually made of a nearly water-equivalent material such as Lucite (Fig. 69-8). It is designed to degrade the beam energy point-by-point by variable amounts so that the distal edge of the beam conforms to the shape of the target plus a suitable margin. The compensator is the final element in the nozzle. The air gap between the patient and the compensator is minimized to reduce the penumbra by moving the snout close to the patient. The aperture and compensator for each beam are designed by the planning system and the design information is used to fabricate these devices using computer-controlled milling machines.

FIGURE 69-8 • An acrylic compensator, which is patient-specific and designed to conform the distal edge of the beam to the target plus margin.

In computing the compensator thickness at each point, the water-equivalent path length to the distal edge of the target along the ray from the source of protons through the compensator point to the distal edge is determined. The surface irregularities and tissue inhomogeneities are taken into consideration in this computation. The compensator design algorithms used in current treatment planning systems are simplistic and do not adequately account for changes in the lateral scattering of protons caused by heterogeneities and surface and compensator irregularities.

Because the SOBP width for a passively scattered beam is designed to be constant across the entire field, passive scattering provides no control over dose distribution proximal to the target. For a target with highly irregular distal edge, this may lead to a substantial excess volume of high dose proximal to the target.

For scanning beams, proximal and lateral field shaping is achieved by limiting the positions of the spots to within the target regions only. Presumably, there is no need for an aperture. However, because of the substantial size of pencil beam spots, some consideration is being given to the use of apertures (or multi-leaf collimators [MLCs]). There is also no need for a compensator since the energy of spots can be varied to ensure no protons penetrate beyond the distal edge of the target. It is evident that scanned beams lead to lower dose in the proximal regions. The intensities of the spots are optimized to achieve desired clinical goals.

Proton Treatment Planning

The objective of treatment planning is to determine the configuration and parameters of beams that will lead to an optimum dose distribution. The parameters include the number and directions of proton beams. For the PSPT mode, for each beam these also include distal and proximal margins, lateral margin, beam energy (or the maximum proton range), modulation width, and the characteristics of the aperture, compensator, and range shifter. Energy and modulation width are subsequently used to select the modulator and its parameters and the second scatterer. For scanned beam treatments, the parameters include the intensities and energies of the spots and (possibly) their spacing. Most parameters for the PSPT mode are generally user selected, whereas most parameters for the scanning beam mode are determined by computer-aided optimization. In other words, PSPT mode planning is forward, whereas scanning beam mode planning is inverse.

In current practice for conventional treatment planning, a typical proton planning system uses mode-specific parameters to compute a treatment plan showing dose distributions expected to be received by the patient over the course of radiotherapy. The plans are evaluated using dose distributions and dose-volume histograms. Although many of the steps in the proton and photon treatment planning processes are similar, there are significant differences. Some of these differences arise because of the physical characteristics of protons. Others are the result of the greater vulnerability of protons to uncertainties because of inter- and intrafractional variations in anatomy, the approximate values of the Hounsfield units and proton stopping powers in tissues, and the approximations in models to compute dose distributions, especially in the presence of complex heterogeneities. The range of protons, i.e., the exact point where a beam of protons or its subdivisions stop in the inhomogeneous patient, is uncertain.

Because of these issues, the volumes and margins for targets and normal structures used in treatment planning, as described in International Comission on Radiological Units (ICRU) Reports 50 and 62,⁵^,⁶ need to be reconsidered. The concept of planning target volume (PTV) has limitations even for conventional radiotherapy. For instance, assuming that the margins to extend clinical target volume (CTV) to PTV are chosen with appropriate consideration of inter- and intrafractional anatomic variations, the dose volume histogram (DVH) of a PTV represents the worst case scenario: clinical target volume is guaranteed to receive no less than the minimum dose to the PTV. It does not, however, reflect actual dose distribution received by the CTV, which may move around from time to time and from day to day within the PTV.

The situation for protons is still more complex. Anatomic variations, whether along or perpendicular to the beam direction, and other sources of uncertainties mentioned above can affect the depth of penetration. These factors must be considered in designing margins and field-shaping devices, as well as in designing and evaluating treatment plans as a whole.

Treatment Planning Considerations for Passively Scattered Proton Therapy

An uncertainty in range means that field-specific distal and proximal margins must be assigned to the CTV to ensure coverage of the CTV along the path of each beam. These margins have been estimated to be of the order of 3% of the depth of the target. The estimates are based on clinical experience and measurements but may be smaller for simple, relatively homogeneous geometries and significantly larger for other cases, such as where metal artifacts on CT images exist or where heterogeneities in the path of protons may change inter- or intrafractionally.

Compensators designed simply to conform the distal edge of the proton dose distribution with the distal edge of the target assume that the patient’s anatomy is invariant over the course of radiotherapy and remains aligned with the compensator in day-to-day positioning. However, positioning uncertainties and changes in inhomogeneities relative to the target volume in the path of a proton beam would affect the depth of penetration and the conformity of the dose distribution to the distal and, to a lesser extent, proximal edge. To ensure coverage of the target in the presence of misalignment of the compensator with the anatomy and the variations of anatomic structures of significantly different densities, compensators are smeared.⁷ The smearing process essentially reduces the width of the higher thickness regions of the compensator to allow protons to penetrate more deeply even when adjacent higher density tissues move into their path. Smearing and margins for range uncertainty ensure coverage of the target, albeit at the expense of higher dose to normal tissues distal to the target. Furthermore, smearing would normally necessitate an increase in the modulation width to ensure that dose to the proximal edge is not compromised. Smearing also coincidentally reduces the consequences of inadequate accounting for lateral scatter in current proton planning systems.

Targets that move because of respiration present additional challenges for PSPT planning. It has been demonstrated that if proton planning for such targets is based on conventional CT images, the dose distributions seen on the treatment plan may be a poor representation of the dose distribution actually received by the patient, leading to target underdosing and normal-tissue overdosing.⁸ There have been recent attempts to incorporate respiration-induced motion into proton therapy planning. For example, four-dimensional (4D) CT data sets, comprising a sequence of three-dimensional (3D) CT data sets, one set for each phase of the respiratory cycle, may be used to design the motion-integrated internal target volume (ITV). The compensator design is then based on the so-called maximum intensity projection (or MIP) image of the ITV in which each voxel within the ITV is set to its maximum intensity in any one of the phases.⁸ An alternative approach reported by Engelsman et al.⁹ also uses the 4D CT. In it, one compensator is designed for each phase of the 4D CT. The union of all the compensators represents the final composite compensator. Either strategy ensures that protons will penetrate sufficiently deeply to cover the target adequately regardless of its position. However, actual dose distribution behind the target may be significantly higher compared with what would be seen on the resulting treatment plan. It is highly desirable that gated or breath-hold treatments be used for proton therapy if the intrafractional motion exceeds a certain threshold, e.g., 0.5 cm.

Lateral margins depend on the anatomic variations orthogonal to the beam direction and are generally determined in the same manner as the PTV margin for photons. To this margin is added the width of the penumbra from 50% to approximately 90% to 95% to define the aperture margin.