13 Modern Principles of Brachytherapy Physics
From 2-D to 3-D to Dynamic Planning and Delivery
Brachytherapy is now a century old. It has grown through many generations and evolved into a very efficient and uniform way to deliver radiation to tumors. A complete week, with approximately 30 hours of lectures, was devoted to cover physics and the technical aspects of brachytherapy at the American Association of Physicists in Medicine (AAPM) Summer School in 2005. The book1 about this event certainly represents one of the most comprehensive reviews of the field, and many textbooks and thousands of scientific papers have also been devoted to this topic. Nevertheless, the majority of the concepts reported in the literature were developed in a different era, when three-dimensional (3-D) imaging was limited and dose planning was based on “systems” that tried to prevent hot spots and suboptimal dose distributions in the absence of other safeguards. Clearly, many of the paradigms of brachytherapy deserve to be revisited.
Why 3-D in Brachytherapy?
Many treatment centers have reported the practical and clinical benefits of 3-D planning after transitioning from 2-D to 3-D. As demonstrated by several studies, in the case of gynecologic treatments, much higher bladder and rectal doses are found when using the CT information. The minimum dose (Dmin) to the cervix target volume is lower than the dose to point A in each case. Similarly, dose to normal tissue is generally reduced and smaller volume is irradiated when 3-D planning is introduced. Image fusion of CT and MRI data enabled improved target volume definition in 3-D–based planning.2
CT-based planning allows for some automation in the anatomy delineation and catheter definition. For instance, automatic catheter reconstruction in prostate HDR treatment can easily be achieved.3 The time required for the catheter reconstruction process using an autoreconstruction method is significantly reduced compared with the manual approach on CT, and is reduced even more when compared with film-based reconstruction.
Radiation Sources and Dose Calculation
This section is not intended to replace a radiation physics course. For that purpose, we refer the reader to an excellent book by Baltas et al.,4 which goes into much more detail or the handbook published by Mayles et al.5 We will, however, recall the basic concepts necessary to introduce modern brachytherapy radiation sources and dosimetric concepts. In particular, this should help the reader to relate known quantities such as kerma and dose to the AAPM Task Group 43 (TG43) formalism.6 Note that in this chapter, our interest is with photon-emitting sources.
Radioactivity and Interactions
Thus, after a period of time t, the remaining number of atoms, Nt, is given by:
where λ is the radioactive decay constant (probability to undergo a nuclear transformation per unit of time) and N0 the initial number of atoms. The half-life, 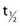 corresponds to the time necessary for one half of the initial number of atoms to decay or N = N0/2. It also corresponds to half of the initial activity. Solving equation 1, one finds:
corresponds to the time necessary for one half of the initial number of atoms to decay or N = N0/2. It also corresponds to half of the initial activity. Solving equation 1, one finds:
Defining A0 as λ N0, one can also predict the activity at time t:
where NA is the Avogadro constant and M is molar mass. The right term of that equation applies to a pure isotope.
in which A is the atomic mass number and NA is the Avogadro constant. For photon sources, the relevant interactions are Compton, photoelectric, Rayleigh, and pair production, although for most modern brachytherapy sources, this last process is negligible. Each one has its own cross-section, which are combined to give the linear or mass attenuation coefficients (total cross section).
Dosimetry
in which dEtr is the average transferred energy, µtr/ρ is the mass energy transferred coefficient and ψ is the energy fluence (related to the photon fluence as previously defined). Note that the mass energy transferred coefficient is related to the mass attenuation coefficient through the fraction of the total energy (E) that is transferred per unit of path length.
in which µen/ρ (or µab/ρ) is the mass energy absorption coefficient and g is the mean fraction of energy not spent in collision with orbital electrons. In the context of charge particle equilibrium, the dose (D) is equal to the Kcoll and thus can be related to the photon fluence and energy fluence.
in which fas is a factor correcting for attenuation and scattering when the air around the equilibrium mass is replaced by water (adopting the notion of Baltas et al.4). In a more compact form, this equation can be written as:
Average mass energy absorption coefficient can also be used based on the effective source energy. Note that the ratio of the mass energy absorption coefficient is sometime referred to as the factor (fmed).7
Source Specification and Air Kerma Strength
The distance r must be large enough compared with the extent of the source so that it can be treated as a point source. The indices δ in the air-kerma rate was included in the revised TG43 publication8 to remove very low-energy photons produced close to the surface of the capsule or source cladding. These do not contribute to the dose beyond the first millimeter. The use of δ is similar to that of the air-kerma rate constant, γδ, as defined by the International Commission on Radiation Units and Measurements (ICRU). Values of γδ for the most commonly used isotopes can be found here.9 The SI unit for the air-kerma strength is cGycm2h−1 (µGym2h−1). The symbol U is also commonly used in practice and publications, but it is not an SI unit. At a distance (r) of 1 cm, the air-kerma strength of a perfect point source will give a dose rate in cGy/h in air. The air-kerma strength can be related to the apparent activity of a source by the air-kerma rate constant (we are not advocating the use of apparent activity):
For a PSI, the integration from t = 0 to infinity of equation 21 is a constant related to the source half-life, and the total deposited dose is given by:
Revised TG43 Formulation
By definition, equation 26 results in gX(r = r0) = 1. Thus, the variation in the radial dose function is given relative to that reference point. The removal from this equation of the geometric dependence and any variation in θ also has to be taken into account, as we describe later in this chapter. The radial dose function gX(r) is obtained as function of r from measurements or more commonly by the Monte Carlo calculation. The 1-D or 2-D values are extracted using the corresponding point source or line source geometric function. The values are tabulated and used in treatment planning.
To conclude this section, let us summarize by providing the possible revised TG43 equations:
Equations 28 and 29 are recommended. Note that the first 1-D formulation uses the line source geometric factors and radial dose function. This is the recommended 1-D formulation by the AAPM TG43 because it provides the greatest accuracy at small distances for sources that are not perfect point sources. It is, however, not systematically implemented in commercial planning systems. A source can be considered as a point source for distances more than three times the active length of the source (r > 3L). The second 1-D formulation uses the point source approximation for the geometric factor. This is the 1-D formulation used in most planning systems at this time. Historically, there was also a 1-D formulation that averaged the anisotropy factor not only over all angles, but also over all distances to obtain the anisotropy constant ψan.
Clinical Considerations
Modern Brachytherapy Photon Sources
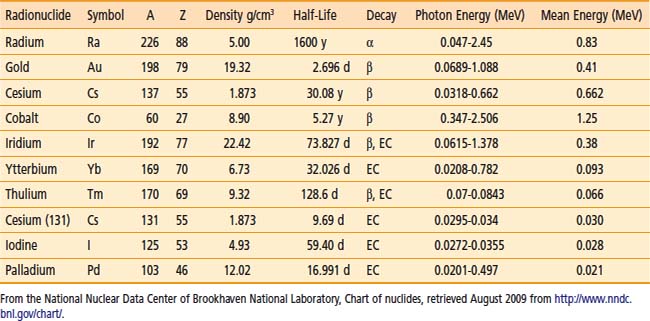
A number of isotopes have been used throughout the years for cancer treatments. Examples are given in Table 13-1. For radiation protection (safety) reasons, a number of nuclides are not used anymore, such as radium, which has a very long half-life and emits high-energy photons. Furthermore, high-energy sources have a large mean path length. Although this generates relatively uniform dose in the target volume, the penetrating photons are a disadvantage for the protection of OARs compared with the low-energy sources, such as iodine 125 (125I) for example.
Thus, to produce sources that are easier to handle, to shield, and to subsequently dispose of, the industry has moved toward lower-energy and shorter-half-life isotopes. All the nuclides shown in the bottom portion of Table 13-1 are good examples of isotopes used in modern brachytherapy. For permanent prostate interstitial brachytherapy, the patient body itself constitutes enough shielding, in the energy range of 20 to 30 keV, that the patient is not a danger to his family (even though the “as-low-as-reasonably-achievable [ALARA] principle recommends not to hold small children directly on one’s lap for an extended period). The half-value layer of lead needed for 125I photons is 0.025 mm. The latest incarnation of this trend is unequivocally the electronic sources. The latter are miniature x-ray generators, which produce no radiation when the current is off and are sufficiently low-energy to be used in a regular radiology suite.
Permanent Seed Implants
In PSIs, multiple sources or seeds are used. The exact number and their positions within the treatment volume are the results of the planning process. It depends on the prescription dose, the seed strength, and the treatment volume. In this type of treatment, the seeds are left permanently, as the name describes, within the human body. Thus the radioisotopes are encapsulated in a biocompatible shell. Three radioisotopes are used clinically in PSI: 125I, palladium 103 (103Pd) and more recently cesium 131 (131Cs). According to the brachytherapy source register at the RPC,10 16 seed models meet the general AAPM dosimetric prerequisites at this time. For most seed models, the shells or capsules are made of titanium (Ti), a well-known material in the medical field. All clinically used seeds are between 4.5 and 5 mm in physical length and 0.8 mm in diameter. The shell is usually laser-welded at the tips of the capsules. This can have an affect on the anisotropy function of the seed resulting from the extra attenuation of photon exiting through the welding. Encapsulation provides protection to body tissues or fluids, which are never in direct contact with the radioisotopes. Therefore, the seeds can be used in patients that have allergies to iodine, for example. Furthermore, the Ti melting point is 1941 K. Therefore, they are highly resistant to all types of sterilization procedures and to cremation as well, should a patient die within a few months after the implants are placed.
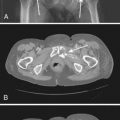
Three very different designs are portrayed in Fig. 13-1. The first (left) is a 125I seed. The radioactive material is deposited on a silver rod (red) in a welded Ti capsule (black). This design is typical of the 6711 seed and of the SelectSeed. The total seed length is 4.5 mm for both models. The middle seed is model 2335 103Pd seed. The radioactive material is deposited on three polymer beads (red) on each side of a 1.2-mm long tungsten marker (yellow). A welded, double-wall Ti capsule is used (black) to seal the components. The total seed length is 5 mm (4.25 mm active length). Finally, the last design represented is the IBt OptiSeed 1031L 103Pd seed. The innovative part of this seed is its biocompatible polymer shell made only of carbon and hydrogen (orange). A 2-mm long gold marker (yellow) is placed in the middle of the 5-mm long seed. On each side of the marker, a palladium tube (red) 0.7 mm in length emits the low-energy photons. The active length is 3.7 mm.

FIGURE 13-1 • A Monte Carlo study of seed design on the interseed attenuation in permanent prostate implants.
(From Afsharpour H, D’Amours M, Coté B, et al: A Monte Carlo study on the effect of seed design on the interseed attenuation in permanent prostate implants, Med Phys 35:3671, 2008.)
Let us stress that many more designs exist.11 Because of the internal configuration of the marker and nuclides, and the use of different marker and encapsulation materials, it should be obvious to the reader that each seed will have specific photon emission patterns: intensity as a function, polar angles, and energy spectrum. Therefore, we emphasize once more, that TG43 dosimetric parameters are different for each seed.
Iodine 125
The half-life and photon energies are given in Table 13-1. The specific activity of 125I is more than 600 GBq/mg4 and iodine seeds are currently being used not only for PSIs (with air-kerma strength between 0.4 U to 0.8 U) but also eye plaque (up to 5 U).
Cesium 131
Note that this isotope possesses the shortest half-life of the three isotopes available for PSI. Thus the initial dose rate for 131Cs is higher than that of 103Pd and 125I.13,14 It is thus more susceptible to postimplant edema. Finally, the controversies remain in comparing the dose to both the prostate and the OARs with different radionuclides, in particular when the biologic effective dose is considered.15
High-Dose-Rate and Pulsed-Dose-Rate Brachytherapy
Ytterbium 169
Battista et al.16 have proposed ytterbium 169 (169Yb) as an alternative radionuclide for brachytherapy. Its specific activity is approximately 2.5 times higher than 192Ir, making it a good candidate for production of a small source of high strength. With an average energy of 93 keV, 169Yb would lower the shielding requirements of an HDR brachytherapy room. This nuclide is produced in a reactor from the reaction 168Yb(n,γ)169Yb. Because 169Yb composes only 0.13% of natural Yb element, an enrichment process must be performed. 169Yb decays by EC in excited states thulium 169 (169Tm). Return to the ground state proceeds via gamma emissions (45%) or internal conversion (55%). Seventy-four γ-ray transitions (from 63 keV to 782 keV), 13 characteristic x-rays, and more than 100 different electron energies (the most probable all being less than 130 keV) are emitted. The most common γ-rays are 63.12 keV (44%), 109.8 keV (17.5%), 130.5 keV (11.3%), 177.2 keV (22.2%), 198 keV (35.8%), and 307.7 keV (10%). A potential downside of this isotope from a clinical perspective is that its half-life is less then 50% of that of 192Ir, and it therefore needs more frequent source change.
Thulium 170
This radioisotope is made by neutron activation through the reaction 169Tm(n,γ)170Tm. The abundance of stable 169Tm is 100%. 169Tm is the rarest of the rare-earth elements (although found in quantities similar to silver) composing less than 0.01% of the ores from which it is extracted.17 Thus obtaining high purity materials is expensive. The decay of 170Tm proceeds mainly (99.87%) via β− decay. It can decay directly to the ground state (81.6% of the time) with a maximum beta energy of 968 keV (average energy of 323 keV). 18.3% of time the β− decay will go to the first excited state and the associated beta energy will be lower (maximum of 883 keV, average of 290.5 keV). Final decay to the ground state can proceed directly by gamma emission of 84.25 keV photons, 2.48% of the time or via internal conversion leading to a series of six x-rays and six low-energy electrons. Apart from the 84.25 keV, the total x-ray emission probability is small at 6.25% for energies ranging from 7.42 keV (2.93%) to 60.96 keV (0.12%).
However, it should be noted that because of the low gamma and x-ray emission intensities, the air-kerma rate constant for 170Tm is approximately 200 times lower than 192Ir.9 Thus, a thulium source might very well be limited to PDR applications. Moreover, the effect of the high-energy electron emitted in beta decay probably needs to be taken into account both in terms of bremsstrahlung emission18 and also in terms of the possibility of insufficient encapsulation thickness to stop all betas. In such a case, an increased dose could be expected in the first few mm outside of the source capsule.
Electronic Sources
The latest in the field of brachytherapy are electronic sources.19 These are composed of a miniature x-ray source, which emits x-ray only when the tube current is on. Xoft has commercialized the first electronic sources, Axxent, and these are Food and Drug Administration–approved for specific treatments. It is a low-energy source of 50 kV. As such, the dose fall-off is greater with electronic sources than 192Ir. Because the energy is lower than current radiology type devices, the body itself constitutes sufficient shielding. This allows for treatment personnel to be present in the room with the patient during treatment. So in principle no special (shielded) treatment room is needed. Finally, there is no radioactive waste handling.
As with any x-ray device, an electronic brachytherapy source produces a continuous energy spectrum. For the Axxent model, that spectrum has a mean energy at or lower than that of 103Pd,20 but a dose rate high enough for HDR treatments. The x-ray tube is 2.25 mm in diameter and the complete assembly is 5.4 mm in diameter. The tube is water-cooled and disposable after usage.
Three-Dimensional Image Acquisition for Planning
3-D imaging modalities, mainly US and CT but also MRI for prostate21,22 or gynecologic imaging23,24 and functional imaging such as magnetic resonance spectroscopy (MRS)25
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


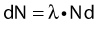
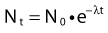
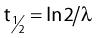
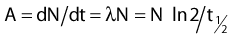
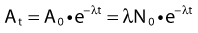
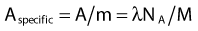
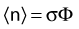
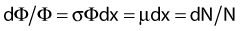
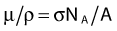
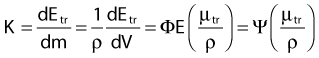
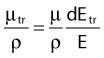
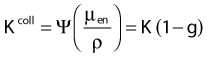
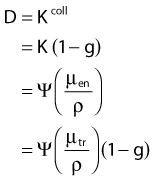
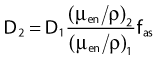
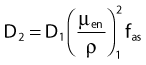
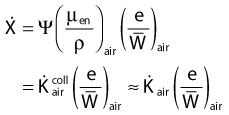
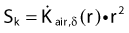
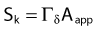
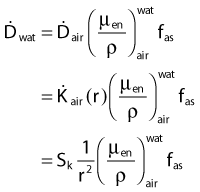
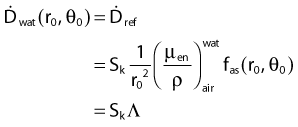
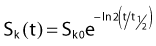
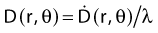
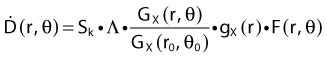
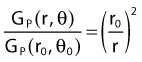
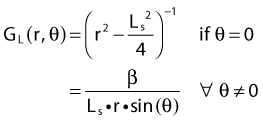
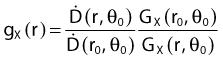
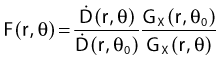
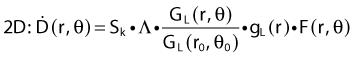
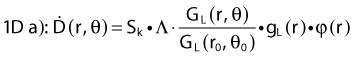
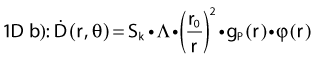
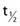 = 11.50 days). 131Cs also proceeds by EC in 131Xe with a half-life of 9.69 days. This last process results in low-energy x-rays between 29.46 keV and 34.42 keV. There is no gamma emission.
= 11.50 days). 131Cs also proceeds by EC in 131Xe with a half-life of 9.69 days. This last process results in low-energy x-rays between 29.46 keV and 34.42 keV. There is no gamma emission.