Fig. 17.1
As the dose delivered to a tumour increases, so does the probability of tumour control (TCP). However, the resultant increase in dose to surrounding healthy tissues increases the normal tissue complication probability (NTCP). Balancing TCP against NTCP is known as the therapeutic ratio
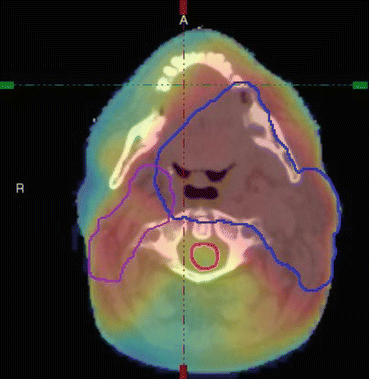
Fig. 17.2
An axial slice from a radiotherapy treatment plan of a patient treated for head and neck cancer. The Primary PTV and nodal volume are contoured along with the spinal cord (red). The colour wash indicates the dose distribution
Typically, the 3D dose distribution to each delineated structure is characterised using a dose-volume histogram (DVH). A differential dose-volume histogram reports the volume (absolute or relative) of a structure which receives a specific dose (Fig. 17.3 top). Modern treatment planning systems usually calculate histograms with a bin width of ≤ 0.1 Gy. More commonly, histograms are displayed as cumulative dose-volume histograms where, for each dose level, the volume of the organ or structure receiving at least that dose is reported (Fig. 17.3, bottom). These values are commonly reported as Vx where x is the relevant dose, e.g. V60 is the volume of a structure receiving at least 60 Gy.
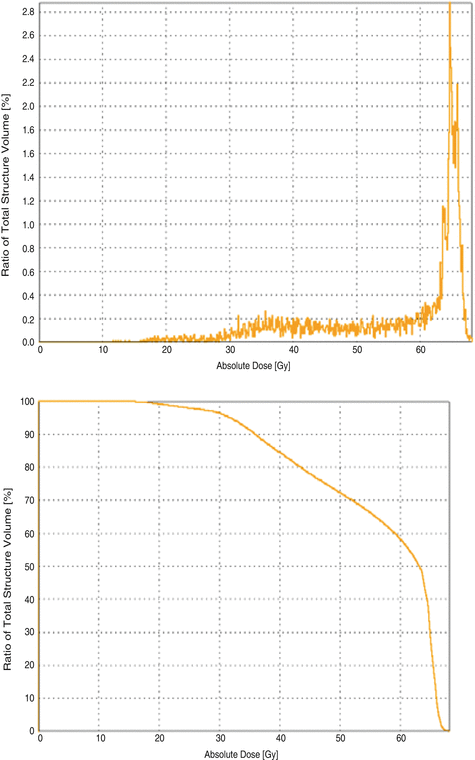

Fig. 17.3
Examples of differential and cumulative dose-volume histograms (DVH) for a normal tissue structure close to the tumour
Describing the dose distributions in order to model the response of the structure has been explored widely. The QUANTEC report published as a supplement in International Journal of Radiation Oncology, Biology and Physics [38] provided a comprehensive report summarising the published data on the dose-volume response for 16 organs at risk whilst considering the limitations of the data and providing recommendations on how to improve future data collection and analysis. Commonly, the dose measure is quantified as a metric such as maximum or mean dose or volume of the structure receiving a specified dose (V(x)). Once developed and validated, these metrics can be used prospectively as constraints during the treatment planning process. Each treatment plan is assessed prior to treatment in order to ensure safety and to evaluate the likely therapeutic success and risk of complication. In order to assess this risk, the concept of normal tissue complication probability (NTCP) has been developed. It is the probability that a given dose distribution to a defined tissue or structure will result in a quantifiable (unfavourable) response in the patient. The dose-response of tumours to radiation is characterised using a sigmoidal response, and this shape of response is translated as the basis for NTCP models. However, whereas in the case of a tumour where the dose is (ideally) homogeneous, in the case of a normal tissue, the dose distribution is ideally inhomogeneous with as much tissue as possible being spared. The result of this is the challenge of which metric to plot on the abscissa.
17.1.1 NTCP Models
A range of NTCP models have been developed; the most widely known and perhaps the most regularly used is the Lyman-Kutcher-Burman (LKB) model. This model comprises an empirical model of dose-response as a function of irradiated volume [35], the reduction of a dose-volume histogram to a single metric [32] and parameter fits for individual organs at risk [5] based on the tolerance doses summarising clinical knowledge by Emami et al. [18]. Originally, the Lyman model was developed for particle therapy where dose distributions fall off steeply and essentially result in uniform dose D to a percentage of the organ with little dose to the remainder. The tolerance dose parameter TD 50 (1) or TD5(1) is the 50 or 5 % probability of experiencing toxicity where the whole structure is irradiated. The power law is employed to account for fractional irradiation.
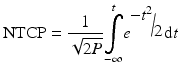
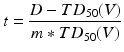
where
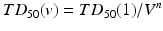
TD 50 (V) is the tolerance dose for a partial volume V. The parameter m is the standard deviation of TD 50(1) and n indicates the volume effect of the organ being assessed. n = 0 indicates a completely ‘serial’ structure, where the maximum dose dominates outcome and n = 1 is a ‘parallel’ structure where the mean dose is related to the outcome.
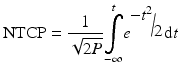
(17.1)
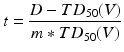
(17.2)
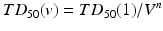
(17.3)
17.1.2 Dosimetric Data Reduction-Summary Measure
In reality, the dose distribution to an organ at risk is likely to be inhomogeneous. In this case, a reduction is required to translate the inhomogeneous dose distribution to a single metric that results in the same radiation response as a corresponding homogeneous dose distribution. The most commonly used metric is the generalised equivalent uniform dose [47]. Originally developed as the equivalent uniform dose to tumours [46], the concept was extended to include normal tissues. The formula is usually written as
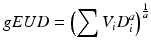
where D i is the dose in the ith bin of the DVH and V i is the volume of tissue receiving dose D i and a is the volume parameter and is equivalent to 1/n.
(17.4)
Alternative models which consider the functional architecture of the organ/structure have also been employed. The functional subunit (FSU) [63] is a concept which describes either an anatomically defined substructure such as the nephron of a kidney or the largest group of cells which continue to function provided one clonogen survives. In an analogy to electrical circuits, FSU are arranged in either series, parallel or a combination of both (Fig. 17.4). If the architecture of a structure is serial, then lethal damage to just one functional subunit can impair function. An example of this is the spinal cord where damage to a short section of the spine can lead to serious side effects. Consequently, constraining the maximum dose delivered to any part of the structure is used to protect a serial structure from damage. In contrast, organs arranged in parallel have a reserve, whereby a number of functional subunits may be damaged before there is any loss of function. This is true of the liver. In this case, it is the mean dose to the structure that is generally considered. In many cases, the true architecture of an organ is mixed, and the manifestation of the side effects differs.
The relative seriality model [28] proposed by Kallman considers the dose distribution on a voxel-by-voxel basis and calculates the probability of local damage for each voxel in the treatment plan incorporating the dose-response curve with a tolerance dose D and slope γ before combining these probabilities and weighting according to the parameter S which defines the ‘relative seriality’ of the organ with a value of 1 indicating a highly serial structure, whilst parallel structures have an s value close to 0.
Niemierko et al. [48] proposed a critical volume model based on FSU. A parallel architecture model proposed by Jackson et al. [25] considers the phenomenological response of functional subunits describing the probability defined in terms of the tolerance dose and slope of the dose-response. Whilst each of these models attempts to model the dose-response relationship for an individual structure, the LKB model is still dominant in the clinic.
17.1.3 Quantification of Toxicity Data
Each organ or normal tissue structure exhibits an individual profile of one or more radiation-induced responses. For example, the rectum is incidentally irradiated (as a normal tissue) in the course of treating a number of pelvic malignancies, including the prostate and endometrium. Rectal toxicity may manifest as loose stools, rectal urgency, pain and frequency in addition to the well-studied endpoint of rectal bleeding [42]. It is thought that the underlying pathophysiology for each of these symptoms may be different. In order to understand the relationship between dose (and other contributing factors) and toxicity, the quality of the toxicity data is vitally important. A number of validated reporting schemes exist. Many of these include questions for specific normal tissues and specific endpoints. However, the fact that there is more than one scoring scheme available suggests that none are perfect and inconsistencies will occur when comparing data and models based on different schemes. In addition, it is important to ensure that the length of follow-up of a patient cohort is sufficiently timed to include all likely events. A cross-sectional analysis at 3 years is likely to yield different results to a cumulative analysis up to 3 years. All of these factors must be taken into account when building models as there is potential for ‘garbage in, garbage out’.
17.1.4 Parameter Fitting
Conventionally, models are obtained by fitting a sigmoidal-shaped curve to a measure of dose to predict toxicity. This is achieved using data from retrospective cohorts of patients. Commonly, multivariate logistic regression [24] is performed where the model to predict probability of toxicity is comprised of coefficients describing the contribution of individual explanatory variables to the final model [15]. Maximum likelihood estimation (MLE) [27] is employed to establish the coefficients using optimisation algorithms such as conjugate gradient descent. The outcome predicted by the model is compared to the known outcome, and the error is minimised to find the optimal parameter fit. Logistic regression assumes that the variables in the model are independent and uncorrelated. Since DVH data is neither of these, careful consideration is required on the use of logistic regression. As a result, dosimetric information can be reduced to a summary metric such as mean dose resulting in a compromise of the data included in the model. Statistical techniques of cross validation and bootstrapping are employed to ensure generalisability of the models.
17.1.5 Challenges of NTCP Modelling
Despite many studies on large, high-quality datasets, predicting NTCP remains a challenge. Figure 17.5 presents results from the UK MRC-RT01 study [21]. A retrospective analysis of implementing dose-volume constraints to dose distributions for the rectum following prostate radiotherapy demonstrated that the more constraints a patient failed, the more likely they were to experience toxicity. However, 1/3 of patients who met all the constraints still reported moderate or severe rectal toxicity. There are many potential reasons for this.
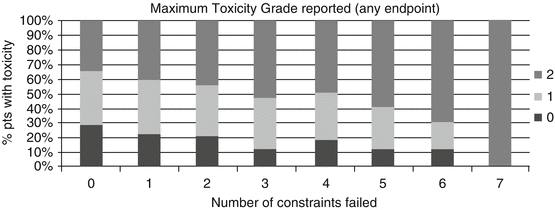

Fig. 17.5
Maximum grade of combined late rectal toxicity, none (0), mild (1) and moderate/severe (2), compared to the number of dose-volume constraints (applied retrospectively) failed [21]
1.
In addition to the dosimetric response of normal tissues, many other factors contribute to the incidence of toxicity, including patient characteristics, such as comorbidities or previous treatments which may modify the dose-response and other treatments including chemotherapy which have the potential to cause side effects but may also affect the dose-response of an organ [29].
2.
Preliminary data is emerging to indicate that the response of normal tissues is partly determined by genetic susceptibilities. Genome-wide association studies (GWAS) have so far shown inconsistent results when associations between toxicity and single nucleotide polymorphism (SNPs) have been investigated [1].
3.
Currently, the 3D dose distribution to an organ is summarised and/or reduced to provide dosimetric information. However, this often results in the loss of spatial information. It is known that many organs contain substructure which is inherent to organ function. A classic example is the kidney [13] where dose to the nephrons is known to be important.
4.
Dosimetric data for an organ at risk relies on the contouring of the structure on the treatment planning system. Institutional protocols should be in place to ensure consistency of outlining. However, definitions may vary between institutions, and this is particularly important when applying a model to data from another institution [20].
5.
What you see is not what you get (WYSINWYG). In addition to contouring consistency, most NTCP studies use the treatment planning scan to define the organ at risk. Great care is taken at each fraction of radiotherapy to ensure that the treatment plan is reproduced and that the target is irradiated accordingly. However, variation in normal tissues is not necessarily accounted for, so unless an accumulated dose, based on daily imaging, is constructed, there may well be a difference between the dosimetric data reported from the treatment plan and the actual dose to the normal tissue being modelled [26].
Awareness of these challenges and, where possible, incorporating them into the NTCP model will improve the robustness and the generalisability of the resultant models.
17.2 Why Should We Consider Machine Learning Approaches to Dose-Volume Effects?
Machine learning brings a new toolbox to the challenges of predicting NTCP. The concept of allowing a non-linear model to develop without an ‘a priori’ definition of the relationship between input variables and outcomes removes bias from our limited understanding of the response of normal tissues to radiation and enables us to uncover new information. Many of the considerations for predicting NTCP using machine leaning are common to the different ‘flavours’ of machine learning. As discussed, the data available includes dosimetric data, patient characteristics, previous health history, other current health conditions (comorbidities), systemic therapy (chemotherapy) and surgery. Little is known about the interaction between these different types of information, and therefore, the flexibility of being able to include variables without understanding higher-order interaction terms is a genuine advantage of machine learning. Many of the publications to date that predict NTCP from dosimetric variables present the data in the form of volume receiving (x) Gy or a reduction of the dose-volume histogram to EUD. The bins of the histograms for an individual patient are known to be highly correlated. Depending on the uniformity of the radiotherapy protocol for the cohort under observation, there is usually an inter-patient correlation to consider. Machine learning approaches are generally well placed to cope with such interactions.
17.2.1 Feature Selection
Feature/variable selection can be regarded as either a preprocessing step or an integral part of model fitting. Where the existence or strength of correlation between individual features and toxicity is unknown, a wide range of possibilities will need to be included in the original input data. It is important to also consider interactions between variables that may contribute to the predictive power of the model.
Advantages of preprocessing feature selection include reduction of model complexity, decrease in computational burden and improved generalisability of unseen data [16].
A wide range of methods for variable selection are available, and a useful summary on this is found in [49]. Within the literature for predicting NTCP using machine learning, undoubtedly one of the most popular is principal component analysis (PCA). Principal components are uncorrelated linear combinations of variables in a given dataset, which account for the variance in the input features in a dataset without reference to the corresponding outcome data, i.e. unsupervised learning. Ideally, data with the same outcome class naturally cluster together, and the clusters are separable from each other. PCA is a particularly attractive feature for DVH-based analysis where variables are known to be highly correlated and has been coupled with conventional statistical models such as logistic regression as well as machine learning methodologies.
A large proportion of the variance in a dataset is often described by the first few principal components. PCA enables reduction to a lower dimension allowing visualisation which can inform researchers on the complexity of the input-output relationship of the data and consequently on the appropriate choice of model. The reduction of dimensionality results in the ability to visualise high-order data. One of the earliest studies using PCA to predict NTCP was published by Dawson et al. [12] who considered PCA for two different organs at risk. PCA was chosen in order to consider all the bins of a DVH without having to reduce to a single metric, such as mean dose, or summary metric such as EUD. The first cohort included 56 head and neck patients where data from the parotid glands was used to predict xerostomia (dryness of the mouth) 12 months after radiotherapy. The dosimetric data was characterised as a cumulative DVH with 1 Gy bins (84 bins in total). The first two principal components explained 94 % of the variance in the DVH. When these were plotted against each other (Fig. 17.6) and labelled according to outcome class, there was a clear separation between the classes indicating that outcome classes were potentially linearly separable. The 1st principal component was shown to correspond to a larger percentage of parotid volume treated to 10–60 Gy. This was approximated as the mean dose, which is commonly used as the constraint to the parotid gland [14]. Logistic regression was applied to the first three principal components in addition to patient sex, age and diagnosis. Only the first principal component was significantly associated with toxicity.
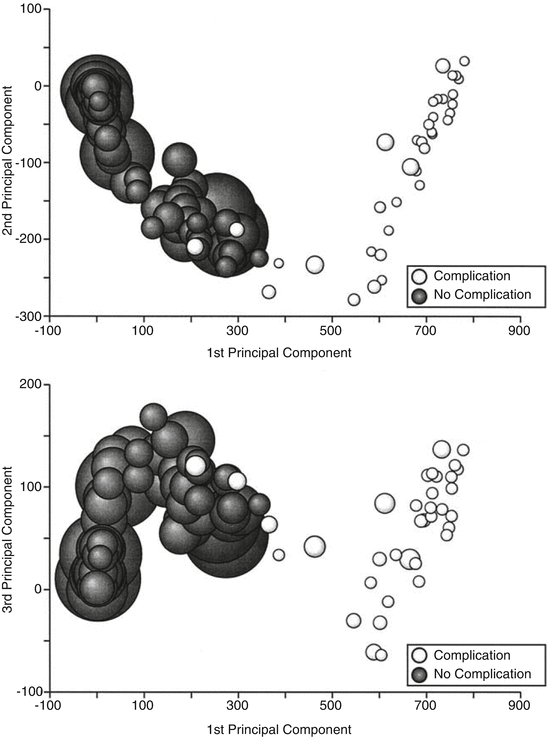

Fig. 17.6
Demonstrating linear separability of data describing xerostomia based on parotid gland dose distributions (Taken from Dawson et al. [12])
In contrast to these clear-cut results, the other cohort studied was 203 patients who received radiotherapy to either partial or whole liver. Initial PCA analysis of the DVH (again 1 Gy bins of the cumulative DVH) showed separated clusters for patients where the whole liver was irradiated vs. those who received partial liver radiotherapy. Subsequent PCA excluded patients who received >20 Gy to >90 % of the liver volume, reducing the number of patients to 138. The first two principal components were plotted along with the Lyman NTCP model however no separation between clusters was observed. Despite this result the results of logistic regression including the first three principal components and relevant clinical factors demonstrated that only the first principal component was significantly associated with toxicity.
Following on from the work by Dawson, Bauer et al. [2] explored the use of PCA to quantify rectal bleeding in a cohort of prostate cancer patients treated with radiotherapy. As with the previous study, the intention was to reduce the degrees of freedom in the rectal dose-volume histograms to characterise those with or without toxicity. The paper gives a very helpful explanation of the background to PCA.However, unlike other studies on this subject, the authors state that direct implementation of PCA forfeits ease of interpretation as the individual principal components do not represent unique dose-volume combinations that are associated with outcome, although they acknowledge that some insight into relevant features of the DVH may be ascertained. Consequently, the authors propose the use of a varimax rotation, an orthogonal rotation applied to the subset of principal components that account for most of the variance in the dataset. The varimax rotation maximises sparseness of the subset, and only small regions of each mode (component) remain large allowing identification of specific regions of the DVH. However, the process reintroduces correlation which must be accounted for. A subsequent study by Sohn et al. [56] applied PCA to a cohort of 262 prostate cancer patients who were treated with a different treatment planning technique. Here, the conventional four-field ‘box’ beam arrangement was used. However, an adaptive approach based on imaging over the first week of treatment was employed. Fifty patients reported late rectal bleeding CTCAE v. 3 ≥ G2. As with the previous study, the bins of the cumulative DVH provided the input features; however, in this case, the bin width was 0.1 Gy resulting in 850 variables. 93.5 % of the variation was accounted for by the first two principal components. This increased to 96.1 % when the 3rd principal component was also included. The 1st principal component was correlated with much of the DVH, whilst the 2nd principal component was considered to be related to the volume of the rectum in the high-dose region where all of the treatment beams overlapped. The 3rd principal component was correlated with 2 distinct regions 40–45 and 70 Gy. Again, this was attributed to the treatment technique. Although the first three principal components accounted for most of the variation and were interpretable, when plotted no obvious clusters were observed. Univariate logistic regression analysis indicated that only the 2nd principal component was significantly associated with rectal bleeding. Multivariate models including the first two and the first three principal components were both shown to be statistically significant. The first principal component was shown to correlate both with mean dose and independently with V60, whilst the 3rd principal component correlated with the maximum dose.
The use of PCA to predict both rectal and bladder toxicity following prostate radiotherapy was reported by Skala et al. [55]. In this study, responses from 437 patients to a postal questionnaire (using RTOG grading) sent out following radiotherapy were analysed. The DVH data were characterised in 1 Gy bins and were analysed using both absolute (volume in cc) and relative (% of volume) descriptors. PCA results were tested for correlation with toxicity ≥G2 using the Mann-Whitney test, but none of the principal components was statistically significant. Standard descriptors of dose Dmax, V50, V60 and V70 were also tested, and again none were found to be statistically significant. The incidence of rectal toxicity ≥G2 reported in the study was very low (~3 %), and therefore, the lack of statistical significance is unsurprising. Bladder toxicity was slightly higher (~10 %); however, historically, correlating dosimetry with toxicity of the bladder has been much more challenging with variable results [62]. It is important to emphasise that the lack of correlations is most likely related to the data itself and that the use of a more sophisticated technique will not necessarily improve the results.
Another study by Vesprini et al. [61] describes using the same methodology as Skala on a cohort of 102 prostate cancer patients who received hypo-fractionated radiotherapy (3 Gy per fraction) to predict the incidence of both acute and late bladder and rectal toxicity. Association between dosimetric descriptors, both conventional and principal components, and toxicity was assessed using Pearson’s correlation coefficient. None of the dosimetric predictors for the rectum were correlated with acute rectal toxicity. However, the bladder V40, V50 and the 3rd principal component were correlated to acute genitourinary (GI) toxicity. In contrast, all of the conventional descriptors and the 1st principal component were statistically significant for late rectal toxicity, and none of the bladder variables were related to late genitourinary (GU) toxicity. The interpretation of principal component 1 was not presented, but the results were shown to overlap with those provided by the conventional dosimetric variables. It was suggested that principal component results did not necessarily add extra information on the relationship between the rectal DVH and rectal toxicity.
A more recent publication on the use of PCA in radiotherapy incorporates spatial information into the relationship between dosimetry and toxicity. Liang et al. [33] used PCA to identify patterns of irradiation of the bone marrow in the pelvic region which were likely to increase acute haematologic toxicity. White blood cell count nadir was used as an indicator for acute haematological toxicity in a cohort of 37 patients treated with chemo-radiotherapy for cervical cancer. The dose distribution for each patient was standardised by mapping each treatment planning CT, via deformable registration, onto a pelvic bone template. The corresponding dose distributions were interpolated and mapped onto the template. The dose to each voxel in the standard image was calculated and considered as a predictor variable. The template ensured the same number of voxels for each patient, and these voxels were sampled systematically, left-right, anterior-posterior and superior-inferior, to form a row vector for each patient containing 44,146 elements. For each patient, the same element referred to the same voxel. Clearly, this dataset would benefit from dimensionality reduction. As with some of the previous studies, since all of the variables were measured using the same scale (Gy), PCA was performed with the covariance matrix. Of the 36 non-zero eigenvalues with corresponding eigenvectors, 5 were statistically correlated with acute haematologic toxicity using univariate logistic regression. Although the first PC accounted for over 20 % of the variation, the principal components shown to be correlated to toxicity were the 12th, 23rd, 24th, 25th and 31st principal components, and combined together, they accounted for just 4.2 % of the variation in the dataset. The results of the regression were used to test if the resultant dose space was related to toxicity. Acute haematological toxicity was defined by dichotomising the white blood cell nadir as <2,000/μml for no toxicity (n = 23) vs. ≥2,000/μml for toxicity (n = 14). Difference maps of the dose distribution were projected onto the pelvic bone template for those with/without the defined toxicity and compared with the voxels which were shown to be statistically significant in the regression model. There was good agreement between the two assessments (Fig. 17.7). This mapping approach allowed the visualisation of important anatomical regions of active bone marrow which could be avoided using intensity modulated radiotherapy (IMRT).
Fig. 17.7
The top row indicates areas of pelvic bone marrow correlated to acute haematologic toxicity dichotomised as white blood cell nadir <or > /2,000 μml. The bottom row represents the regression coefficients produced after PCA (Taken from Liang et al. [33])
17.2.2 General Considerations
The use of machine learning is often favoured where the underlying relationship between the data is unknown and there is a need for future prospective evaluation of data. This is exactly the case for normal tissue complication probability. Generally, the dose-response of organs at risk is not well quantified, particularly for specific endpoints. This needs to be improved in order to optimise the use of available technology and to further increase the rate of successful cancer treatments. In the meantime, we prospectively evaluate every treatment plan going through the clinic, and the development of knowledge-based tools to facilitate this process is highly desirable. Therefore, the ability of a trained model to generalise unseen data is imperative. Techniques to ensure this include cross validation and bootstrapping which reduce the dependency of a final model on a specific training dataset. The use of an independent (relevant) test set, to measure model performance, once the model has been finalised, should also be regarded as standard practice. It is important to appreciate the extent to which the model can generalise. If a model is trained on data from a centre, then a well-built model should be able to reflect the toxicity experience of that centre. However, it may not be able to predict toxicity for a similar cohort of patients from a neighbouring centre where subtle changes in treatment technique, toxicity reporting or patient demographic may render the model irrelevant.
Since the intention of radiotherapy is to keep the incidence of toxicity to a minimum, the balance of toxicity/no toxicity in the dataset may be very unbalanced with only a small number of patients reporting toxicity. Whilst this is generally good news for the patient, it is a challenge to model building. A number of approaches exist to try to account for this. Firstly, the ratio of toxicity/nontoxicity cases should be standardised across training groups, for example, stratified cross validation, and in the independent test set. It is also possible to promote the number of cases within the dataset for the underrepresented class [30].
17.2.3 Assessing Model Accuracy
The performance of NTCP models is often quantified using the receiver-operator curve (ROC) analysis which quantifies the ability of a continuous variable to predict for a dichotomised outcome by considering every possible cut-point in the continuous variable and calculating the resultant sensitivity and specificity [57]. Sensitivity (true positive rate (TPR)) and specificity (true negative rate (TNR)) are calculated from the confusion matrix (contingency table) of predicted vs. known outcome classes for a given dataset and cut-point. The resultant plot of sensitivity against 1-specifity for all possible cut-points is known as the ROC curve. The area under the curve (AUC) indicates the probability that the model would rank a randomly selected positive case higher than a randomly selected negative case. Alternatively, Matthews correlation coefficient [37], also calculated from the confusion matrix of a binary classification problem, is an alternative approach to quantifying the predictive power of the model. It is regarded as being particularly useful in situations where the classes are of different sizes.
It is defined as
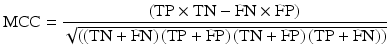
where TP is the number of true positives, TN true negatives, FN false negatives and FP false positives.
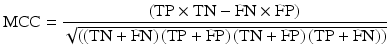
(17.5)
An MCC value of 1 indicates a perfect classification, 0 a random classification and −1 a wholly inverted classification.
Once the model has been finalised, it is useful to evaluate the importance of each input feature in making the prediction. Some model types, for example, decision trees, lend themselves to interpretation, whilst others such as artificial neural networks are regarded as impenetrable black boxes. Even in this case, it is possible to investigate the role of each input by using techniques such as leave one out (LOO) where data for each input feature is removed and the effect of the predictive power of the model reassessed.
17.3 Classic Machine Learning Approaches
There are many flavours of machine learning; however, most of the literature related to predicting NTCP is from the more established techniques. These can be broadly separated into supervised and unsupervised learning approaches including. Conventionally, a model relates a number of variables to an outcome or classification; this is supervised learning. In contrast, unsupervised learning finds patterns and groupings among the input variables only; these groupings should then naturally reflect the classification of the data. The following sections consider the use of supervised learning approaches, artificial neural networks and support vector machines, and unsupervised learning techniques for prediction of NTCP.
17.3.1 Artificial Neural Networks
Artificial neural networks (ANNs) are one of the classic machine learning approaches dating back to the seminal work of McCulloch and Pitts [39]. With the analogy of the way the human brain works, it is tempting to think that the knowledge of an experienced clinician or medical physicist can be easily transferred. It has been a popular choice for applications relating to predicting the response of normal tissues to radiotherapy. One of the earliest papers was published by Munley et al. [44] who trained a feedforward, back-propagation, neural network to predict symptomatic lung injury following radiotherapy. Ninety-seven patients were included in the neural network of which 25 had a clinician assessed symptomatic lung injury. Patients with a number of tumour sites were included. Although 2/3 of the patients were treated for lung tumours, the inclusion of other tumour sites increased the diversity of the dose distributions and confounding factors in the training cohort. The neural network had 29 inputs corresponding to pretreatment features which described a range of variable types including patient characteristics (age, race, sex, smoking status); disease characteristics (tumour site and central lung tumour); baseline assessment (heterogeneity of SPECT scan adjacent to and away from the tumour, diffusion capacity of carbon monoxide (DLCO), forced expiration volume in 1 s (FEV1), haemoglobin, chronic obstructive pulmonary disease (COPD)); chemotherapy and dosimetry which included dose-volume histogram reduction using both the Lyman [36] and Kutcher method [32]; volume of lung receiving 10 Gy (V10), V20, V30, V40, V50, V60, V70 and V80; and the full and effective dose to lungs and the lung volume. Each input was scaled 0–1. The architecture included two to five hidden nodes and a single output node each with a sigmoidal activation function. Training was performed using the leave-one-out approach where each patient case was taken out and the neural network retrained. Training was terminated when the ROC analysis was maximised. The final result was an AUC of 0.833 +/−0.04. This result was compared with multivariate logistic regression which resulted in an AUC of 0.813 +/−0.064 and the dose-volume histogram reduction method of Kutcher which yielded an AUC of 0.521 +/−0.08. The influence of each input variable was assessed by retraining the neural network with the leave-one-out approach applied to each variable and ranked by assessing the deterioration in AUC after a fixed number of iterations. The top five variables were found to be heterogeneous SPECT (apart from the tumour), haemoglobin, histogram reduction (Kutcher), COPD and age, the first three of these were also the top three ranked variables using multivariate logistic regression. It is clear from these results that combining dosimetric and clinical information enabled the most accurate prediction of toxicity. The use of a leave-one-case-out approach to train the neural network is likely to result in overfitting, but using a leave-one-input-out approach to investigate the contribution of individual features allowed useful insight into the prediction of toxicity. Following on from the early work by Munley, Su et al. [58] used data from 142 non-small-cell lung cancer patients from the same institution (Duke University Medical Centre) to predict radiation pneumonitis ≥ grade 2 also using ANN. Thirty-one of these patients were included in the previous study. This study compared 3 different approaches to segmenting the training and testing data and only considered 8 dosimetric input features describing the volume of lung receiving 10 Gy stepping up in increments of 10 Gy up to 80 Gy. As previously, a leave-one-out approach was employed to train ANN_1 on all but one case and testing on the omitted case. The predictive success was characterised by AUC which was reported to be 0.85. Two further approaches were tested. ANN_2 used 2/3 of the available data for training and 1/3 for testing. The allocation of data was essentially random as patients were ordered in alphabetical order in terms of their last name. Finally, ANN_3 was intended to improve the quality of the training data by ensuring the maximum variation in input parameters for the cases reporting toxicity where once again 2/3 of the cases were used for training. The respective AUC for ANN_2 and ANN_3 were 0.68 and 0.81 demonstrating that careful consideration of the cases provided for training can have a statistically significant improvement in predictive accuracy. The ability to generalise the unseen cases should also be improved compared to the leave-one-out method. A comparison with standard predictive models of V20 and mean lung dose and LKB model (TD5/5 23 Gy, m 0.17 and n 0.86) [5] demonstrated that each of these models yielded an AUC of around 0.5, no better than chance, although the authors acknowledged that a fairer comparison would have been to derive the parameters for their own data using maximum likelihood estimation.
In 2007, Chen et al. [8] reported results for a larger cohort of lung cancer patients from the same institution, Duke University Medical Centre, North Carolina. Radiation-induced pneumonitis (≥ grade 2) was reported in 34 out of 235 patients, all of whom were treated using 3D conformal radiotherapy. ANNs were constructed using an algorithm that successively pruned and grew the input features and hidden nodes, using a training-validation cohort to assess improvement (or otherwise) of each successive iteration. To avoid local minima, weights and bias were trained from five randomised initial sets and the lowest error used overall. Weights were constrained to ensure reasonable responses between input variables and outcome. For example, weights connecting dosimetric variables were constrained to have a positive value only. The authors acknowledged that this approach prohibits a complimentary subtractive effect between variables but suggest that this will safeguard against detrimental overfitting. 93 potential input variables were available. Dosimetric information included V6 to V60 in 2 Gy increments and gEUD varying from 0.4 to 4 in increments of 0.1. The mean dose to the heart was also included. Since many of the dosimetric variables are highly correlated, the training rules ensured that once a variable had been incorporated into the model, no other highly correlated variables (>0.95) were eligible for inclusion in the model. The inclusion of non-dosimetric variables was justified by citing previous analysis of normal tissue response which was shown to be modified by interaction with chemotherapy [40] and age [34]. A wide range of non-dosimetric variables, similar to the previous publications, were included covering patient demographics, treatment information and pre-radiotherapy assessment of lung function. A tenfold cross-validation approach was used to ensure that the results were generalisable, whilst a 2nd approach using all patient data for training was developed for prospective testing. Leave-one-out analysis was used on this 2nd architecture to assess the influence of individual-chosen variables. Comparison of models was performed using ROC analysis. For the ANN trained using cross validation, the optimised architecture containing only dosimetric variables resulted in an ROC of 0.67 for the independent test when non-dosimetric variables were added to the model construction; this improved to 0.76. Each of the ANN developed using cross validation contained different variables; however, the authors highlight that often highly correlated variables were represented in each model. The model trained for prospective testing included 6 variables, V16, gEUD a = 3.5, gEUD a = 1, forced expiration volume in 1 s (FEV1), carbon monoxide diffusion capacity of the lung (DLCO%) (both of which were assessed prior to radiotherapy) and induction chemotherapy. All input features except FEV1 and induction chemo were shown to be individually statistically significant. It is clear from these results that different parts of the dose distribution were included in the final model despite dosimetric correlation being constrained. This result suggests that different parts of the dose distribution are important in predicting toxicity. We will consider this again with later publications.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree