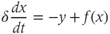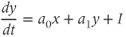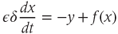Chapter 9
Modeling the Dynamics of Gonadotropin-Releasing Hormone (GnRH) Secretion in the Course of an Ovarian Cycle
Frédérique Clément and Alexandre Vidal
INRIA Paris-Rocquencourt Research Centre, Domaine de Voluceau, Le Chesnay, France
Laboratoire de Mathématiques et Modélisation d’Évry (LaMME), Université d’Évry-Val-d’Essonne, Évry, France
9.1 Introduction
9.1.1 GnRH surge and the triggering of ovulation
In mammals, ovulation is a key limiting step of reproductive success. Ovulation is the process by which a fertilizable oocyte is released from a fully mature (ovulatory) ovarian follicle and collected into a fallopian tube. Depending on the species, either one (in mono-ovulating species) or several (in poly-ovulating species) oocytes are ovulated within an ovarian cycle. The triggering of ovulation is controlled by the central nervous system, first on the hypothalamic level, and then on the pituitary level (Figure 9.1).
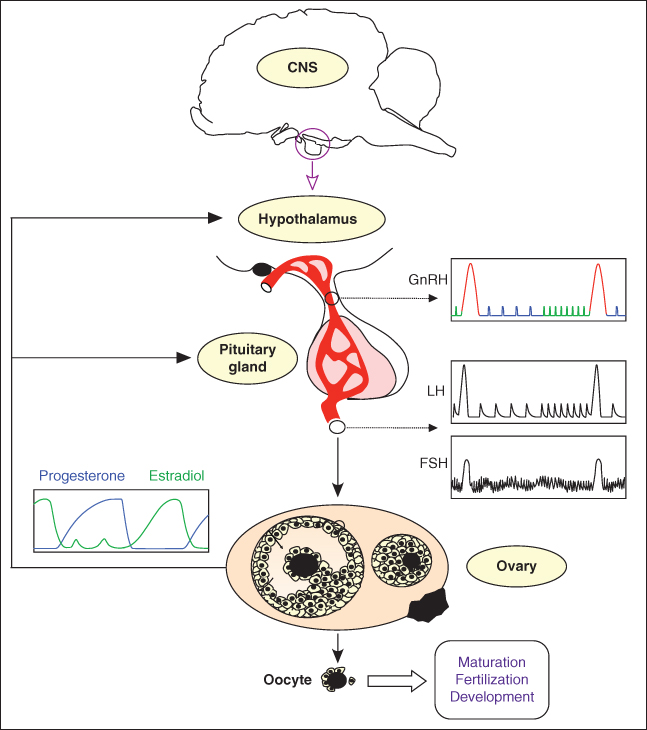
Figure 9.1 Neuroendocrine control of ovulation. The release of one or several oocyte(s) is a cyclic event that results from the endocrine dialogue between the hypothalamus, pituitary gland, and ovaries. The hypothalamic hormone GnRH (gonadotropin-releasing hormone) is the master neurohormone controlling reproduction. During most of the ovarian cycle, the pattern of GnRH secretion is pulsatile. The release of GnRH into the hypothalamo-pituitary portal blood induces the secretion from the pituitary gland of luteinizing hormone (LH), which also follows a clear pulsatile pattern, and follicle-stimulating hormone (FSH). LH and FSH control the development of ovarian follicles and their secretory activity. In turn, hormones released by the ovaries (steroid hormones such as progesterone and estradiol or peptide hormones such as inhibin) modulate the secretion of GnRH, LH, and FSH within entangled feedback loops. In females, the GnRH secretion pattern dramatically alters once per ovarian cycle, in response to the time-varying levels of ovarian steroids, and switches to the GnRH surge characterized by a massive release of GnRH (surges in two successive cycles are shown in red). In turn, the GnRH surge triggers the LH surge, whose duration is shorter. The GnRH-induced LH surge finally brings about ovulation – the release of fertilizable oocytes from ovarian follicles.
In every mammalian species investigated so far in a physiological setting, ovulation is triggered by the so-called GnRH surge, which corresponds to a dramatic and quite sudden increase in GnRH secretion from the usual pulsatile secretion regime and which brings about a surge in the secretion of luteinizing hormone (LH) (Christian and Moenter, 2010). In spontaneous ovulators (such as human, sheep, or cattle, for instance), the GnRH surge is triggered in response to the ever higher levels of estradiol secreted by the ovaries in the follicular phase of the ovarian cycle, without any other driving force than the neuroendocrine feedback loops within the hypothalamo-pituitary-ovarian axis. In some spontaneous ovulators (such as rat), the GnRH surge is, nevertheless, subject to a circadian control and can only occur during a specific time of the day (this circadian control ultimately explains the distribution of the rat ovarian cycles between 4-day or 5-day cycles). In induced ovulators (such as cat and rabbit, but also llama and camel, for instance), the GnRH surge is triggered by mating. Yet, the mating-induced GnRH surge can only occur in a steroid-favorable environment of high estradiol levels, so that the endocrine dialogue between the ovaries and hypothalamus is still a master-piece of the ovulatory process.
9.1.2 GnRH secretion regimes
GnRH neurons are space-specific and scarce (of the order of 1 to a few thousands) neurons located in different hypothalamic areas (mostly in the preoptic area). Like the other neuroendocrine neurons that regulate the anterior pituitary, they are endowed with a very long secretory process that reaches the median eminence, where GnRH is released. The usual pattern of GnRH secretion in both males and females is pulsatile; each GnRH pulse results from at least partial synchronization within the GnRH neural network. How this very slow (on the order of the hour) network behavior emerges from fast individual neuronal dynamics is a fascinating question that is still unsolved and that we will not deal with in this chapter; we will take for granted that the default regime of GnRH secretion is pulsatile. We will rather focus on the equally fascinating question of how the GnRH secretion pattern switches from a pulsatile background regime to a surge regime back and forth. We will see that this question raises other corollary ones, and especially: how is the alternation between pulses and surge connected with the ovarian dynamics, and how is the frequency of pulses altered along an ovarian cycle (Figure 9.2).
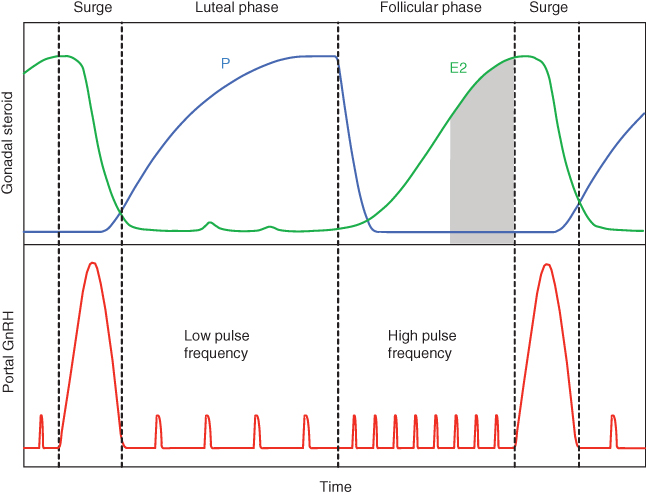
Figure 9.2 Schematic patterns of estradiol (E2) and progesterone (P) plasma levels and GnRH levels in portal blood through the course of an ovarian cycle in female mammals. The pulsatile secretion of GnRH is periodically interrupted by the ovulatory surge that involves a massive release of GnRH. Each surge is triggered by a prolonged exposure to high estradiol levels in a background environment of low progesterone. Between two surges, the pulsatile phase is split into two successive phases: the progesterone-dominated luteal phase, characterized by a low GnRH pulse frequency, and the estradiol-dominated follicular phase, characterized by a high GnRH pulse frequency. The gray area corresponds to the cumulated level of estradiol at surge onset.
9.1.3 Steroid control of GnRH secretion
The question of the effects of ovarian steroids (estradiol and progesterone) on GnRH neurons can be investigated from different angles according to the species. The most precise neuroanatomical studies have been performed in rodents (mice and rats) and have enabled investigators to draw a quite detailed picture of the circuitry of connections linking the neurons directly targeted by ovarian steroids to the GnRH neurons via possible other regulatory neurons. However, physiological studies intending to dissect in time the effects of ovarian steroids have mostly been undertaken in domestic species, especially in the ewe. This species is particularly useful for studying GnRH secretion rhythms, since (i) it has a large body size allowing repeated sampling of pituitary portal blood and cerebrospinal fluid allowing further analysis of GnRH time series, (ii) the duration of its ovarian cycle (around 21 days) makes it easier to dissect the different steps in the temporal sequence of steroid action, and (iii) it is closer to human ovarian physiology compared to rodents.
In almost all studies dedicated so far to the study of the expression of steroid (nuclear) receptors in GnRH neurons (Rønnekleiv and Kelly, 2005), it has been shown that they do not express progesterone receptor, or type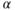 
estradiol receptor (ER 
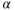), yet they do express the type-
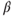estradiol receptor (ER 
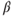) (Hrabovszky et al., 2001; Skinner and Dufourny, 2005). This means that, except for possible acute direct effects of estradiol mediated through ER 
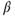(Abraham et al., 2003), the effects of ovarian steroids on GnRH neurons are mostly indirect and involve intermediary neural relays that themselves project onto GnRH neurons.
9.1.4 Experimental setups for portal GnRH withdrawal
Access to kinetic and quantitative GnRH data has been made possible by two original experimental setups (Moenter et al., 1990–1992). First, a tricky surgical technique was developed to implant a dedicated apparatus for pituitary portal blood withdrawal; this technique involves drilling a tunnel in the sphenoid bone between the olfactory bulbs and under the optic chiasma before reaching the pituitary stalk. Second, an experimental protocol inducing an artificial ovarian cycle was designed. This rests on the general principles underlying the studies of endocrine feedback loops, that consist of “cutting” one of the loop branches to decouple the endocrine dialogue between the different organic levels involved in the loop. In the present case, we would like to get rid of the endogenous ovarian steroids and to administer (chemically similar) exogenous steroids in a way controlled both in time and dose. Thus, ewes areovariectomized and then exposed to a regime of steroid mimicking the natural hormone release by the ovaries along an ovarian cycle. They are first given a progesterone implant, to reproduce a luteal-like phase. When the implant is removed, mimicking the occurrence of luteolysis, the ewes are exposed to increasing levels of estradiol, up to the species- and strain-dependent threshold needed to trigger the GnRH surge. Those combined technical and functional protocols have provided most of the information on the control exerted by ovarian steroids on the qualitative sequence of GnRH secretion events and on their quantitative properties, both during the pulsatile and surge regime, that will be detailed in the framework of our dynamical model in the next sections.
9.1.5 The GnRH generator: secreting and regulatory neurons
The whole set of all neuronal (and also glial) cell types involved in the control of GnRH secretion is commonly known as the “GnRH pulse generator.” This includes the GnRH neurons themselves, as well as the regulatory neurons that process the steroids signals and relay them to GnRH neurons. A great variety of neural inputs, either excitatory (e.g., glutamate and norepinephrine), or inhibitory (e.g., GABA – gamma-aminobutyric acid—and endogenous opioids), have been characterized in afferents projecting onto GnRH neurons (Herbison, 1998). However, in the past 15 years, one particular regulatory system has come to the forefront of attention; several lines of evidence have combined to highlight the key role of kisspeptin producing neurons in mediating the steroid feedback control of GnRH secretion, through signaling via the GPR54 receptor (Pinilla et al., 2012). Different subsets of kisspeptin neurons can, at least in rodents, be associated with hypothalamic areas involved differentially in the ovarian feedback exerted either on the pulse frequency in the pulsatile regime (arcuate nucleus, where the expression of kisspeptin is associated with that of neurokinin B and dynorphin that appear to act in a paracrine and/or autocrine way) or on the surge triggering (antero-ventral periventricular nucleus).
9.2 A single dynamical framework for the control of the GnRH pulse and surge generator by ovarian steroids
9.2.1 GnRH secreting system
In the absence of steroid input from the gonads, as in the case in adult ovariectomized ewes not supplemented with exogenous steroids, GnRH secretion consists of regular pulses which occur at a high frequency. Considering the network of GnRH neurons involved in the pulse regime as a single average neuron, we can use the classical FitzHugh–Nagumo (Fitzhugh, 1961; Nagumo et al., 1962) system to represent this default secretion regime concisely:
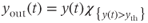
where
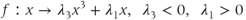
Parameter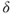 
is assumed to be positive and small. System (9.1a) and (9.1b) is therefore a “slow–fast system”: 
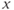is the so-called fast variable and 
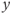is the “slow variable.” Hence, away from the cubic 
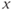-nullcline (represented in Figure 9.3a and c), the trajectories are almost horizontal and fast (slow variable 
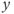remains almost constant since its dynamics is much slower than the 
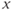dynamics). However, trajectories near the 
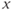-nullcline are slow since the 
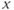dynamics is almost zero and the whole system is under the control of the slow dynamics.
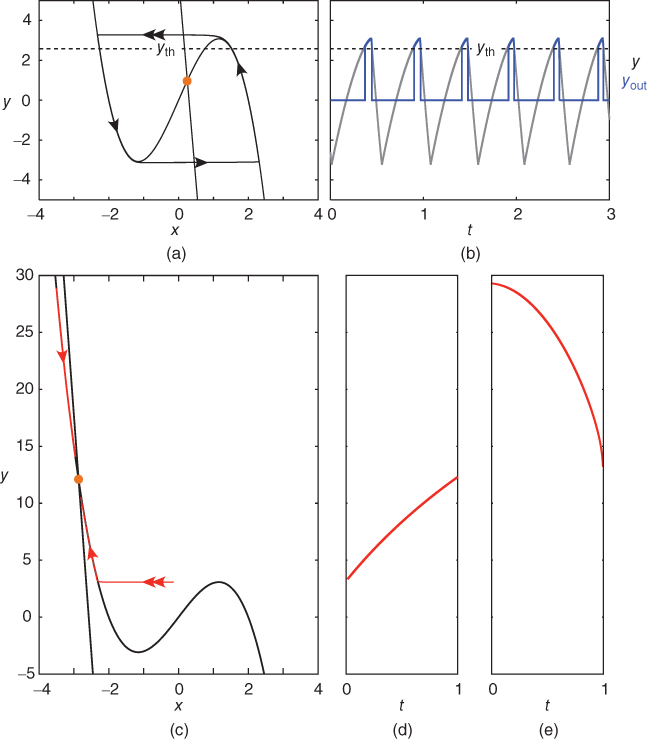
Figure 9.3 Phase portrait of the GnRH secreting system and output 
signal in the pulse regime (a and b) and surge regime (c, d, and e). In each panel (a) and (b), the cubic curve and the straight line represent the 
– and 
-nullcline, respectively. The orange point corresponding to their intersection represents a singular point of the GnRH secreting system. For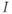 
in an interval of values defined by the other parameters, the GnRH secreting system admits an unstable singular point surrounded by an attractive limit cycle of relaxation type (a). Along this orbit, the generated 
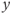signal (gray pattern in panel (b)) is serrated and the thresholded 
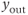signal (blue pattern in (b)) is pulsatile. For greater values of 
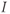, a stable singular point lies on the left branch of the cubic 
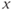-nullcline. Due to the slow–fast property of the GnRH secreting system, the orbits first reach the 
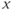-nullcline quickly, and then follow it while tending to the singular point (c). (d) and (e) show the time trace of 
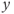along the lower and upper orbits displayed in (c), respectively.
GnRH secretion is represented by the output variable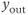 
, that is obtained after thresholding 
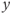. In some sense, the 
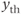threshold can be associated with the critical intracellular calcium concentration that is needed for the secretory vesicles to undergo exocytosis from the neuronal terminals.
9.2.2 Different dynamical regimes of secretion: pulse regime versus surge regime
If we now consider that the default secretion regime can be perturbed by dynamical inputs (entered as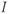 
in Equation (9.1b)), we can switch the secreting system from a pulsatile regime to a surge-like regime. For a given interval of values of 
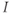, the system (9.1a) and (9.1b) admits an unstable singular point lying on the middle branch of the cubic 
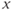-nullcline 
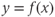. In this case, the singular point is surrounded by a limit cycle of relaxation type (Figure 9.3a) with slow parts along the left and right branches of the cubic 
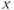-nullcline and fast parts corresponding to back and forth jumps between the right and left branches. Hence, the value of 
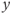along the orbit oscillates around 
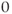and the generated 
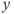signal is serrated. It follows that the model output 
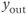, obtained after thresholding 
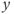, is a pulsatile signal (Figure 9.3b).
For higher values of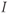 
, the singular point lies high up on the left branch of the cubic 
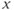-nullcline and is attracting. Therefore, all the trajectories of the system (9.1a) and (9.1b) first reach quickly the left branch of the cubic 
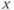-nullcline (under the influence of the fast dynamics), follow this branch to reach the vicinity of the singular point, and then keep tracking this point as long as it lies on the cubic left branch (i.e., remains stable). Such trajectories are represented in Figure 9.3c. The corresponding time traces of variable 
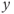are displayed in Figure 9.3d and e: depending on the initial condition, 
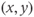may go up or down along the cubic left branch to track the singular point and, consequently, 
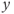may either increase or decrease.
9.2.3 Recurrent periodic alternation between the pulse and surge regimes
Through the ovarian cycle, the dynamical inputs received by GnRH neurons account for the steroid-mediating control exerted by the regulatory neurons. To reproduce both the pulse and surge regimes, we use the following regulating system of FitzHugh–Nagumo type:
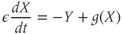
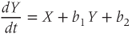
Parameter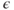 
is assumed to be positive and small, and parameters 
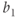and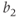 
are chosen so that the system (9.2) admits a relaxation limit cycle (Figure 9.4a). The 
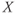signal (time trace of variable 
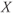) along the limit cycle displays two regimes separated by fast transitions (Figure 9.4b): a slow decrease from 
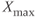to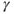 
(
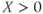) and a slow increase from 
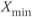to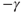 
(
).
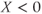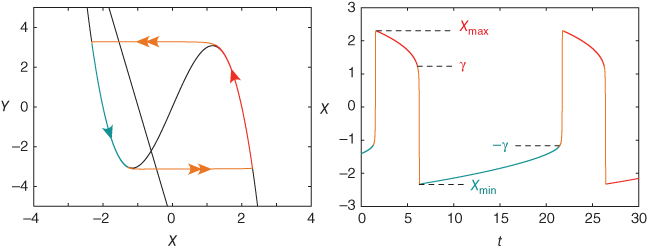
Figure 9.4 Limit cycle of the regulating system and the corresponding time trace of variable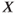 
. The values of parameters 
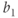and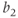 
are chosen so that the regulating system admits an unstable singular point lying on the middle branch of the cubic 
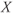-nullcline surrounded by a limit cycle (a). Due to the slow–fast property of the regulating system, the limit cycle is of relaxation type and the periodic 
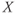time trace is characterized by fast transitions between two main regimes: slow increase from 
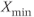to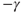 
and slow decrease from 
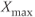to 
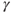(b).
We model the control exerted by the regulating system onto the GnRH secreting system by introducing the linear dynamical input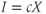 
and coupling the two systems on different time scales (Clément and Françoise, 2007). This yields the global model:
Related posts:
Modeling Endocrine Cell Network Topology
Dynamics of the HPA Axis: A Systems Modeling Approach
Modeling Spiking and Secretion in the Magnocellular Vasopressin Neuron
Ion Channels and Electrical Activity in Pituitary Cells: A Modeling Perspective
A Mathematical Model of Gonadotropin-Releasing Hormone Neurons
Endoplasmic Reticulum- and Plasma-Membrane-Driven Calcium Oscillations
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
