.
where P(D, 1) is the probability of a lesion occurring if the entire organ is irradiated to dose D. This formula was derived using the simple notion that the probability of a lesion not occurring in the organ was the product of the probabilities of its not occurring in all subvolumes of the organ. This model is easily generalized to an inhomogeneous dose distribution, and it has the advantage that the probability of complication is based on the dose response function of a uniformly irradiated whole organ, the most likely form that clinical data of that era would take. However, the mathematical “trick” of using subvolumes does not imply the existence of FSU’s.
Jackson and colleagues developed a similar model for organs with actual FSU’s (Jackson and Kutcher 1993; Jackson et al. 1995). Rather than the production of a single lesion, they modeled a volume element as having suffered a binary level of damage. The endpoint was reached if a sufficient number of volume elements, presumed to be FSU’s, suffered damage. Unfortunately, this formalism requires the dose response function for the FSU in order to determine the organ response. It is not possible to determine the dose response function of a partially irradiated organ based on the dose response of the whole organ. One can see how the division of a so-called serial organ encouraged the mistaken association of these volume elements with FSU’s, as they truly are in an organ with functional reserve.
Both the critical element model and the parallel architecture model are examples of what is known in reliability systems as a k-out-of-N system; the system fails if k of the N elements of the system fail, and is denoted as a k-out-of-N:F. The critical element model is a 1-out-of-N:F system and the parallel model is a k-out-of-N system. A k-out-of-N:G system is good (G) if k of the component remain functional. There are consecutive k-out-of-N systems where a linear system fails if k consecutive components fail. The critical element or serial model is a k-out-of-N system with k = 1. The parallel architecture model of Jackson et al. is a nonconsecutive k-out-of-N system, where N is the number of FSU’s and k is the number that must fail to elicit a radiation complication. Tumors are typically modeled as k-out-of-N:G systems with k = 1. That is, as long as a single clonogen is good, the tumor is viable. More complex models can be made by adding higher dimensions, i.e. two and three dimensional k-out-of-N systems. However, consecutive k-out-of-N systems are mathematically very complex (or at least tedious), and higher dimensional systems have the disadvantage of being simultaneously nearly intractable while having too many independent variates in the model to be statistically useful for modeling normal tissue responses.
3 Fractionation Scenarios
3.1 Conventionally Fractionated Treatments
Image guidance today is primarily achieved with commercially available on-board systems used for daily volumetric imaging in radiation therapy setups such as cone beam CT and megavoltage CT. Open MRI coupled with rotational Co-60 beams has been developed recently and ultrasound imaging is still commercially available. Early versions of daily CT scanning involved scanning on a CT simulator prior to treatment and transferring the patient to a treatment table using a transfer board (Lattanzi et al. 1998). The authors concluded, “With daily isocenter correction of setup and organ motion errors by CT imaging, PTV margins can be significantly reduced or eliminated. We believe this will facilitate further dose escalation in high-risk patients with minimal risk of increased morbidity.” This technique was compared to the use of transabdominal ultrasound in the treatment position for prostate cancer (Lattanzi et al. 1999). The two were found to be “functionally equivalent.”
Thus even as conformal therapy was transitioning to IMRT in the 1990s, efforts to deploy IGRT were already being made. Outside of SRS treatments, these initial efforts were primarily focused on reducing the CTV-PTV margin by reducing set-up variations and imaging the target volume every day. The objective was to increase tumor dose without increasing morbidity. Megavoltage CT was being deployed with a prototype helical tomotherapy for the same purpose (Mackie et al. 1995; Yang et al. 1997). In-room CT was also deployed later with varying success (Owen et al. 2009).
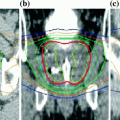
In an extensive study of set-up variations versus the frequency of imaging in IGRT, Han et al. determined the likelihood of a decrease in coverage of the target volume and an increase in NT irradiated volumes when imaging occurred at frequencies of 0, 20, 40, and 60% versus daily (100%) imaging (Han et al. 2012). Even at an imaging frequency of 60%, the lung volume receiving 0.8 Gy per day and the heart volume receiving 1.2 Gy per day increased by more than 20% in 10% of the fractions. The CTV receiving 95% of the daily dose (1.8 Gy) decreased by more than 20% in 5% of the fractions. This is primary evidence that by deploying daily image guidance, the NT doses can be decreased and target doses increased. Complications rates and the types of side effects would not change. Conversely, if the target dose did not change, complication rates could decrease without affecting the types of complications. This was observed by Chung et al. in prostate cancer (Chung et al. 2009).
It is important not to overstate the effect of image guidance. Clearly, an advantage is seen since the NT DVH is shifted to lower doses (and the PTV DVH becomes steeper). However, it is important to acknowledge that part of this shift is a result of reduced margins afforded by daily imaging (IGRT) and part results from improved dose fall-off away from the target due to improved dose delivery technology (IMRT). It is difficult to find in the literature clinical studies that compare similar IMRT techniques with dissimilar imaging protocols. It is the imaging that distinguishes IGRT from IMRT.
3.2 Hypofractionated Treatment
The failure of early hypofractionation resulted from a lack of understanding of radiobiology and the response of normal tissues to radiation. It was believed, or more accurately hoped that morbidity from increases in daily doses could be offset by lengthening the interfraction interval. Furthermore, the biological consequence of increasing the dose per fraction was underestimated. Unfortunately these early attempts were undertaken when field shaping was unsophisticated, volume effects were underestimated, and treatments were frequently delivered using one field per day. By the late 1980s, hypofractionation, often combined with split course treatments, was largely abandoned in the definitive setting (Overgaard et al. 1988; Parsons et al. 1980). Late complications, which are more sensitive to changes in dose per fraction than tumors, increased without a compensating increase in tumor control because the relative dose distributions were not altered.
By sparing normal tissues, IGRT reduces both the dose per fraction and the volume of NT irradiated without reducing the tumor dose. Increasing the dose per fraction to the tumor so that the NT dose per fraction remains approximately constant would still leave a smaller volume of NT irradiated. Using hypofractionation, investigators have tested the hypothesis the NT morbidity will not increase because reduced irradiated volumes will compensate for any increase in dose per fraction. The truth to this hypothesis largely rests on the nature of the volume effect and the pathogenesis of the NT morbidity.
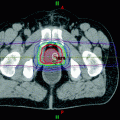
As discussed above, prostate cancer was among the sites where IGRT was deployed early in its history, initially with conventional fractionation. Because doses were being escalated to 80 Gy and higher, overall treatment times were extending beyond 8 weeks. In part to shorten the overall duration of treatment, hypofractionation trials were initiated. In general, the GI late toxicities are similar into those seen with the best conformal or IMRT results. However, there is a strong tendency to report slightly greater GU toxicity in IGRT than in conformal treatments, although severe late GU toxicity is rare.
Rectal toxicity generally includes symptoms of radiation proctitis (urgency, frequency, mucus discharge, pain) or rectal bleeding. Rectal bleeding would not be expected to be very volume dependent, but to depend rather more on dose; however, Wu et al. reported no rectal bleeding in 72 patients treated with a schedule of 16 × 3.4 Gy (Wu et al. 2012). In this report, as in several others (King et al. 2009; Madsen et al. 2007; Pollack et al. 2013), GU toxicity was a greater problem than GI toxicity.
The relatively greater incidence of GU toxicity in IGRT for the prostate can be reasonably explained by the fact that the urethra is in the high dose volume whereas the rectum can largely be excluded from the target volume. Obviously as the target dose is escalated, so are the doses to most GU tissues that are at risk for radiation injury.
A somewhat similar effect occurs in the lung. The relative frequency of toxicity changes in two ways when conformal fields shrink to SBRT fields with the concomitant increase in dose per fraction (Kollar and Rengan 2014). As seen in animal models (Van Der Veen et al. 2016), there is a shift from early to late effects as the volume is reduced. Furthermore, at the higher doses per fraction, the central normal structures become more likely to express morbidity than peripheral lung parenchyma. These effects are independent of yet a third possibility–spatial variation in lung sensitivity as seen in mouse models and attributed to the spatial variation in target structure for radiation pneumonitis (Tucker et al. 1997).
In the CNS, both brain and spinal cord, there appear to be no changes in the types of normal tissue morbidity that result from reducing volumes and number of fractions while increasing the dose per fraction. The obvious exception is that neurocognitive deficits result from large volume treatment of CNS. However, one must still be cognizant of differing sensitivity of different regions. For example, there is some evidence that thoracic spinal cord is less sensitive than the cervical cord. The lumbar cord is also less sensitive, possibly owing to its being myelinated with Schwann cells rather than oligodendrocytes.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree