Human Response to Acceleration
Robert D. Banks
James W. Brinkley
Richard Allnutt
Richard M. Harding
The most reliable instrument for measuring the varied effects of dynamic force on man is man.
—Colonel John Paul Stapp
The first principle is that you must not fool yourself and you’re the easiest person to fool.
—Richard Feynman
INTRODUCTION
Acceleration is the rate of change of velocity. The human response to acceleration depends on magnitude, direction, and duration. The response may be physiological and involve homeostasis during accelerations of low magnitude and long duration. Or it may involve physical injury when the acceleration is high and of short duration. These two general outcomes characterize the way human response to acceleration has been considered, studied, and analyzed.
Low-magnitude, long-duration acceleration involving humans has been termed sustained acceleration. High-magnitude, short-duration acceleration has been termed impact or transient acceleration. In this chapter, we consider the effects of both sustained and impact acceleration on humans and some of the protective strategies associated with each. Because sustained acceleration is encountered by pilots in flight and the major threat is incapacitation, the aim of protection is to prevent a crash and enhance flying ability. Because transient acceleration is encountered during flight operations, escape, or during a crash, the aim of protection is to maintain function, reduce injury potential, and enhance survivability.
These two areas employ very different research methods: one involves mainly human centrifuges and the other, impact tracks and towers. Both approaches have limitations in their ability to simulate real-world events. Models, based on appropriate research, have been developed according to the principles of Newtonian mechanics. We begin with a review of these principles.
Newton’s Laws
Newton’s first law states that a body that is at rest or in motion will remain in that state unless acted upon by a force. A force is a push or pull. For example, an aircraft in straight and level flight is without acceleration if the forces acting on the aircraft are in balance. Similarly, occupants of the aircraft are without acceleration, although they will experience the force of gravity by virtue of lift of the wings.
If an aircraft follows a curving path, such as during a banked turn or upward pitch, a force must act on the aircraft to alter its path (in this case, forces due to lift). In Figure 4-1, the aircraft pitches up due to the forces of lift.
Occupants inside the aircraft also follow Newton’s first law and therefore follow a straight path at a constant velocity unless acted upon by a force. During a banked turn or upward pitch, this force is exerted on the occupant by the seat and floor of the aircraft as illustrated in Figure 4-1.
In Figure 4-2, we illustrate the case of an aircraft pitching down. In this example, the occupant is experiencing a fall to Earth and is also being pulled down by the lap and shoulder belts.
When an aircraft impacts the ground during a crash, the velocity of the aircraft changes abruptly and the aircraft
experiences deceleration. In accordance with Newton’s first law, the occupants of the aircraft will continue at their preimpact velocities until they contact interior aircraft structures that are slowing. In a frontal impact, the first such structure is the restraint system. The next structure will be the instrument panel or control column. Figure 4-3 shows a pilot immediately before the aircraft contacts water. As depicted, during the impact event, the pilot experiences motion within the cockpit interior and contacts forward structures.
experiences deceleration. In accordance with Newton’s first law, the occupants of the aircraft will continue at their preimpact velocities until they contact interior aircraft structures that are slowing. In a frontal impact, the first such structure is the restraint system. The next structure will be the instrument panel or control column. Figure 4-3 shows a pilot immediately before the aircraft contacts water. As depicted, during the impact event, the pilot experiences motion within the cockpit interior and contacts forward structures.
 FIGURE 4-1 Newton’s first law. The aircraft will continue in a straight path unless acted upon by an unbalanced force. When the aircraft follows a curving path, the unbalanced force is due to lift. The occupant will also follow a straight path unless acted upon by an unbalanced force. In this case, the force is the aircraft acting upwards on the pilot (Source: John Martini, BRC). |
Newton’s second law relates force and acceleration, and is expressed as:
 FIGURE 4-2 Newton’s first law applied to an occupant in flight. The force acting on the occupant is downward through the lap and shoulder restraints. The occupant will tend to rise out of the seat (Source: John Martini, BRC). |
 FIGURE 4-3 Newton’s first law applied to an occupant during a crash. The occupant will continue at the precrash velocity during the event until encountering objects forward of the initial position. In this case, these objects include the restraints, controls, and the instrument panel. As seen from within the aircraft, occupant motion appears to be forward (Source: John Martini, BRC). |
We can see from Newton’s second law that when acceleration increases so does force, and vice versa. When a force is applied to an occupant through the seat or restraint, the occupant experiences both acceleration and force. In the case of frontal impact with terrain, the occupant experiences acceleration and force due to contact with the restraints and forward cockpit structures.
Newton’s third law states that any force exerted by one body on another is countered by an equal and oppositely directed force. Because colliding objects usually have different masses, the resulting accelerations will not be the same (Newton’s second law).
Understanding G
The acceleration due to gravity is the same (constant) anywhere on the surface of a planet although it decreases with increasing distance from the center. On Earth, this constant is designated “g” and has the value of approximately 9.81 meters/second squared (m/s2). The force that an object exerts on the Earth’s surface (weight) depends on the mass of the object, but will be the same anywhere on the Earth’s surface for that mass.
The situation is different on other planets. On our moon, for example, acceleration due to gravity is only 1.62 m/s2 and an object will fall to the lunar surface with less acceleration than on Earth. Similarly, the weight of an object on the moon’s surface is less than that of the same object on Earth. A person who weighs 78 kilograms (kg) on Earth will weigh only 13 kg on the moon.
Gravity also affects objects in space that are close to the Earth. Gravity causes spacecraft and their occupants to fall toward the Earth. Spacecraft that have achieved orbital velocity during launch (8 km/s) circle the Earth. Because the Earth’s surface curves away from their path (being round),
the spacecraft and crewmembers cannot close the distance to the surface and so remain in semiperpetual freefall. The “weightlessness” of Earth’s orbit is not the absence of gravity; it is a condition of frictionless freefall.
the spacecraft and crewmembers cannot close the distance to the surface and so remain in semiperpetual freefall. The “weightlessness” of Earth’s orbit is not the absence of gravity; it is a condition of frictionless freefall.
“G” is a measure of the acceleration experienced by a person as a result of a force. Alternatively, it can be regarded as a measure of the force experienced by a person due to acceleration. It is expressed in terms of multiples of the Earth’s gravitational acceleration. One G is experienced during acceleration of 9.81 m/s2 (g).
The relationship of G and acceleration can therefore be expressed as:
Because both “a” and “g” have units of m/s2, and they are divided, the units cancel and G is without units—it is a ratio.
As stated, the G coefficient relates to force. For example, a pilot weighing 70 kg on Earth who is subject to an inflight acceleration of 3 G (and is supported by the seat and restraints), will experience a force that is three times his weight, or 210 kg. It is often more practical to discuss G instead of force or acceleration because force measurements vary with pilot mass, but acceleration does not. Acceleration is convenient to consider in terms of multiples of gravity, and is the term used by aircrew and flight surgeons in the aviation community.
Vectors and Nomenclature
Any quantity that has the properties of magnitude and direction is called a vector. Acceleration, velocity, and force are examples of vectors. G is also a vector. Vectors can be analyzed mathematically using trigonometry. Vectors are described on plots that demonstrate their magnitude and direction. These plots are defined by three mutually orthogonal linear axes: x, y, and z. In aerospace medicine, these plots are considered to be aligned with a forward-facing crewmember as depicted in Figure 4-4.
There has been considerable disagreement about both the conventional placement of axes, and the use of symbols and terms. Basic differences exist between the engineering and aeromedical communities, and within each of these groups. Attempts to achieve uniformity have had mixed results. For example, the Advisory Group for Aerospace Research and Development (AGARD) standard for human acceleration differs from the AGARD standard for aircraft design (in which the z-acceleration axis is reversed and positive downward). It also differs from previous editions of this textbook, which differ from one another. Needless to say, when reading literature involving acceleration it is important to understand clearly the author’s use of these terms and symbols.
To be consistent with the AGARD standard (1), the Table of Equivalents for Acceleration Terminology (2), the Aviation Space and Environmental Medicine Standard (3), and the majority of the Aerospace Medicine literature, the positive direction of each of these axes is here described by “the left-hand rule.” That is, the x-axis dimension is an arrow with the positive direction forward, the y-axis dimension has the positive direction rightward, and the z-axis dimension has the positive dimension upward. This is depicted in Figure 4-4.
 FIGURE 4-4 An axial diagram of the human coordinate system for linear motion. This convention is referred to as the left-hand rule because the placement of the axes mimic a left hand with the index finger pointed forward, the thumb pointed up, and the middle finger directed to the right (Source: John Martini, BRC). |
Aircraft acceleration vectors can be described using this convention. If an aircraft accelerates forward, in the positive direction, the acceleration is denoted by “+ax”. If the direction of aircraft acceleration is upward, the designation +az is used. If the direction is to the right, +ay is used. These symbols are included in the first column of Table 4-1.
The positive direction of the G of an occupant in response to aircraft acceleration is aligned with a. Therefore, when +ax is experienced by the aircraft, a forward-facing occupant experiences +Gx. Otherwise stated, +Gx is caused by acceleration of the seat forward and results in pressure between the seatback and the pilot’s back. +Gy is caused by acceleration of the seat toward the right and results in pressure between the left hip and the left armrest. Positive-Gz is caused by acceleration of the seat upward and results in pressure between the buttocks and the seatpan. These conventions and their counterparts are summarized in Table 4-1. In column 3,
we have included phrases that may aid in understanding these conventions. The symbol “G”, without a subscript letter or prefix symbol, is used when the direction is not specified.
we have included phrases that may aid in understanding these conventions. The symbol “G”, without a subscript letter or prefix symbol, is used when the direction is not specified.
TABLE 4-1 | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||||||||||||
 FIGURE 4-5 Vertical accelerations greater than +1 Gz are termed positive-Gz (+Gz). Any +Gz less than +1 Gz is termed relative-Gz. Any Gz less than zero-Gz is termed negative-Gz (−Gz) (Source: John Martini, BRC). |
Another source of confusion is associated with the +1 G of gravity. An aircraft at rest on the Earth, or in straight and level flight, experiences +1 Gz, and yet there is no acceleration. Therefore, the zero-acceleration reference point in the z-direction is +1 Gz because of gravity. Because any Gz less than +1 Gz is relatively negative, in terms of the effect on an upright human, we use the term relative −Gz to describe Gz stress that is less than +1 Gz, but greater than zero-Gz. When Gz is less than zero-Gz, the expression “negative-G” or “−Gz” is used. Confusion can occur when thinking of less than +1 Gz and greater than zero-Gz. Although this is technically +Gz, physiologically, the body responds as if it is −Gz because the autonomic nervous system is adapted to gravity. Figure 4-5 illustrates this definition.
Frames of Reference
To have proper meaning, the orthogonal linear axes used to describe vectors must be defined according to a “frame of reference.” For example, a person sitting on a train traveling at a constant velocity of 100 Kmph would perceive no speed inside the train and that would be indicated on a vector plot referenced to the inside of the train. An observer positioned in an alternate frame of reference, such as outside the train at a station, would see the person in the train speeding past at 100 kmph, and a vector plot referenced to the station would reflect this velocity. Although describing the same event, the vectors would look quite different because of the different frames of reference.
Any vector, including force, velocity, and acceleration (or G) depends on the frame of reference selected. Sustained acceleration is usually considered within the reference frame of the aircraft interior and occupant space. Transient acceleration is often considered within the reference frame of the Earth.
G is measured using an instrument called an accelerometer, or G-meter. Many aircraft have G-meters mounted on the aircraft and positioned in the cockpit, where they can be seen by the pilots. The G-meter is calibrated to measure acceleration in the aircraft reference frame (az in units of Gz). Similarly, human centrifuges, used to create G on Earth, often have accelerometers mounted near the occupant seat.
PHYSIOLOGY OF SUSTAINED ACCELERATION
Sustained acceleration occurs during normal and aerobatic flight. Because most aircraft maneuvers (such as pitch and banked turns) expose seated occupants to predominantly +Gz, the effects of +Gz on humans has received most of research attention. Negative-Gz has received much less attention, most of it during and shortly after World War II. Gx and zero-G are most relevant to space flight. Gy has only begun to receive research attention with the development of vectored thrust fighters.
This section describes the effects of sustained G in present-day aviation and space flight. Countermeasures are described and limitations in current research are discussed. The need for a revised model of +Gz tolerance is suggested.
Relevant Mechanics
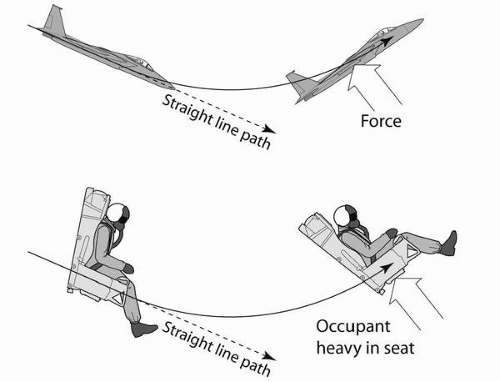
Humans respond physiologically to G. When an aircraft follows a curving path, the velocity changes continuously along the curve (being a vector, although speed may remain constant) and the aircraft experiences acceleration. The acceleration of the aircraft depends on the velocity of the aircraft and the radius of the turn. This is expressed as:
where v = velocity, r = radius of the turn.
If the aircraft occupants are “fixed” to the aircraft, they experience the same acceleration, which is expressed as:
When an occupant experiences +Gz, the associated force is felt as increasing pressure of the buttocks against the surface of the seat. The occupant experiences “heaviness,” and activities, such as lifting an arm, will be more difficult. When relative −Gz is experienced, there is a reduction in pressure on the buttocks and the occupant may feel a rise off the seat. As −Gz increases, pressure of the shoulder and lap restraints is experienced. Ultimately, the occupant may feel suspended by the shoulders and have the sensation of being inverted.
Some aircraft, including civilian aerobatic and military aircraft, are capable of executing large pitch changes at relatively high velocities and can therefore generate high Gz. The magnitude and duration of Gz that an aircraft generates depends on its structural strength and thrust.
Incidentally, Equation 3 can be used to calculate orbital velocity. In stable circular orbit, the acceleration of gravity is equal and opposite to the acceleration due to radius of turn. With a low-Earth orbital radius of 6,700 km, it is easy to show that the turn velocity necessary to create 1 G in opposition to the 1 G of gravity is approximately 8 km/s, which is the low-Earth orbital velocity previously mentioned. This orbital balance of acceleration vectors is a special and important case of weightlessness. Both the freefall concept and the acceleration balance concept are useful and correct in understanding orbital weightlessness.
The Fluid Model
When force is applied to fluid in a constrained volume, the pressure within increases. Pressure is a measure of force (per unit area) transmitted by fluids. For example, squeezing a filled plastic water bottle increases the pressure of the water inside the bottle. If the top is off, the increased water pressure compels the water to squirt out against the constraint of gravity and the resistance of the opening. Similarly, heart contraction during systole increases the pressure within the left ventricle and compels high-pressure blood to open the aortic valve and flow into the aorta.
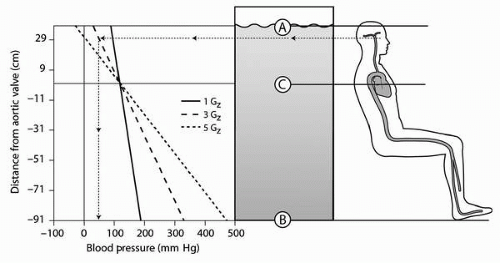
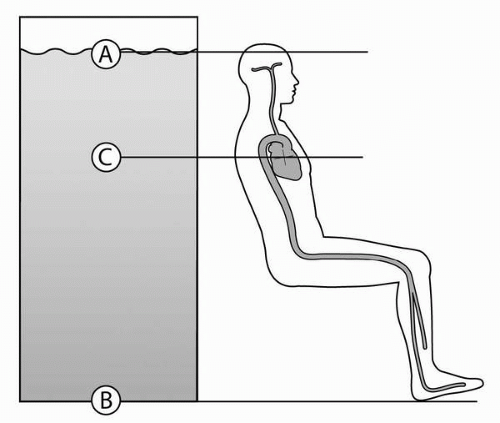
On Earth, the force acting on a fluid at any depth varies with the weight of the fluid above, a principle of hydrostatics. Therefore, pressure increases with increased depth, a fact well known to divers. Referring to the depiction of the column of fluid in Figure 4-6, we expect the pressure of fluid to be less at point A than at point B because there is no fluid above point A. Because fluids are freely mobile, and have no internal rigid structure, pressure is transmitted within the fluid according to Pascal’s principle (which states that a change in pressure at any point in a fluid is transmitted to every part of the fluid).
 FIGURE 4-6 Hydrostatic blood pressure. A seated human figure is depicted next to a fluid-filled container. The hydrostatic pressure of the fluid is zero at the top of the container (A), and maximum at the bottom (B). The pressure is intermediate at point C, which is located between A and B. These principles apply equally to the fluids of the human figure seated to the right (Source: John Martini, BRC). |
Hydrostatic principles apply to all fluids in the body, including the pericardial, pleural, abdominal, and cerebrospinal fluids, and both venous and arterial vascular systems. To the right of the water column in Figure 4-6, we present a seated upright human, and depict the continuous fluid column (cardiovascular system) that extends from the scalp to the feet. Ignoring any pressure generated by the heart, and considering only the hydrostatic pressure of the fluid column, blood pressure at level A is zero, because there is almost no blood above. Blood pressure at the feet (level B) is greatest and equal to the weight of the fluid above. At level C, blood pressure measured at the heart, is intermediate. This component of blood pressure is termed the hydrostatic pressure component.
Pressure due to contraction of the heart adds to the hydrostatic component of blood pressure. If we consider left ventricular contraction during systole, the force applied to the contained blood by cardiac muscle increases intraventricular blood pressure until the aortic valve opens. The increased blood pressure is then transmitted to the aorta and into the arterial system according to Pascal’s principle. This component of blood pressure is termed the dynamic pressure component.
Total blood pressure is the sum of the dynamic and hydrostatic pressures. The measured systolic blood pressure at the heart level of a young healthy adult is typically approximately 120 mm Hg and is the sum of the two blood pressure components. Measurements taken at other vertical locations (e.g., the ankle) will be different.
Numerical estimates of hydrostatic blood pressure can be made using Equation 5, which states:
where p = hydrostatic pressure, ρ = blood fluid density, z = vertical depth of fluid.
For a specific gravity of blood of 1.06, and after converting the units of p from Pascals to millimeters of mercury (mm Hg), Equation 5 becomes:
where p is in mm Hg, and z is in cm.
Equation 6 can be used to estimate the hydrostatic component of blood pressure at different vertical fluid column depths on Earth (+1 Gz). For example, if the vertical distance from the aortic valve to the top of the head is 38 cm, Equation 6 predicts that the hydrostatic pressure at the aortic valve in an upright person is approximately 30 mm Hg (0.78 × 38).
As G increases, the apparent weight (force) of any object increases directly, and this applies equally to fluids. Under increased G, Equation 6 becomes:
Equation 7 can be used to predict G-tolerance, if physiological compensation is not considered. For example, an individual with a vertical fluid distance of 38 cm from the aortic valve to near the top of the head, and having a systolic blood pressure
at the aortic valve of 120 mm Hg, would be expected to have zero systolic blood flow near the vertex at approximately +4 Gz [Equation 7: 120 mm Hg = 0.78(38)(4.0)]. This is a point above which the dynamic systolic blood pressure is unable to oppose the hydrostatic component of the blood. Consequently blood flow to the upper brain would cease.
at the aortic valve of 120 mm Hg, would be expected to have zero systolic blood flow near the vertex at approximately +4 Gz [Equation 7: 120 mm Hg = 0.78(38)(4.0)]. This is a point above which the dynamic systolic blood pressure is unable to oppose the hydrostatic component of the blood. Consequently blood flow to the upper brain would cease.
 FIGURE 4-7 The estimated blood pressures are plotted next to a depiction of a seated human figure using Equations 6 and 7 (assuming a heart-level systolic blood pressure of 120 mm Hg and a 50% average male). To determine the blood pressure at any vertical location, a horizontal line can be run toward the left to the straight line plot of +Gz. The pressure is read directly below on the horizontal axis. The arrowed line provides an example of how to estimate the blood pressure at eye-level during exposure to +3 Gz. Note the high blood pressures in the lower extremities and predictions of head-level blood pressures at +5 Gz that are less than atmospheric (Source: John Martini, BRC). |
Equation 7 can also be used to estimate blood pressures at other locations. Figure 4-7 shows the person seated upright as depicted previously in Figure 4-6. To the left of the human figure are plots of systolic blood pressures versus distance from the aortic valve based on Equations 6 and 7. There are three plots depicted: +1 Gz, +3 Gz, and +5 Gz, and they are based on the approximate dimensions of a 50% average male. Any estimates, using this simple model, will vary with individuals of different sizes. Note the very high blood pressures in the lower extremities at +5 Gz. Similarly, pressures at head level are predicted to be less than atmospheric pressure at +5 Gz. Once again, the underlying assumption is a heart-level systolic blood pressure of 120 mm Hg.
 FIGURE 4-8 A: The estimated systolic blood pressures when the seated individual is reclined during +1 Gz, +3 Gz and +5 Gz exposure. By reclining the seatback, the vertical dimension of the hydrostatic column is reduced and hydrostatic pressure above the heart is reduced. Positive-Gz tolerance is predictably improved (Source: John Martini, BRC). B: The estimated systolic blood pressures when the seated individual is exposed to −1 Gz, −3 Gz and −5 Gz (inverted). This posture depicts increased levels of −Gz. Note the very high predicted head-level systolic blood pressures (Source: John Martini, BRC). |
Equation 7 can be used for other postural orientations such as reclined or inverted. Figure 4-8A depicts the expected blood pressures for a seated reclined individual. Because of the reclined posture, the vertical heart-to-brain distance is decreased, and the hydrostatic blood pressure component is less. Positive-Gz tolerance is predictably
increased. Figure 4-8B demonstrates the effect of inversion, and also the very high head-level blood pressures that can be experienced during −Gz.
increased. Figure 4-8B demonstrates the effect of inversion, and also the very high head-level blood pressures that can be experienced during −Gz.
These predictions agree well with human studies that show a head-level reduction of blood pressure of approximately 30 mm Hg per change of each 1 G (4).
Blood pressure at the head is further lowered if circulating blood volume is reduced. When blood pressure increases during increased +Gz, as it does in the lower (dependent) areas of the body (Figure 4-7), stretching of tissues occurs. As a result of stretching of tissues in the abdomen and lower extremities, a portion of the circulating blood volume becomes unavailable for circulation.
Individual variations in heart-to-brain distances, and differences in blood pressures at the aortic valve, will change these predictions. Therefore, people with smaller vertical dimensions when upright will have an advantage tolerating +Gz when compared to taller people. Elevation of blood pressure at the aortic valve would predictably increase +Gz tolerance.
Human Physiological Response to G
Positive Vertical Acceleration (+Gz)
The brain is very sensitive to cellular hypoxia, which produces rapid loss of brain function. Because oxygen is transported to the brain through the cardiovascular/respiratory system, any interruption in arterial blood flow to the brain leads to cerebral hypoxia. However, loss of function does not occur immediately, when blood flow ceases. There is a reserve time of approximately 4 to 6 seconds before loss of brain function begins (5,6).
Physiological control of blood pressure is based (in part) on the closed-loop baroreceptor reflex. Consisting of upper thoracic and carotid body receptors, efferent and afferent nerves, and centrally mediated responses, the baroreceptor reflex controls blood pressure through activation of the autonomic nervous system. When decreased transmural pressure is sensed in the upper thorax and carotid bodies, the sympathetic nervous system (pressor response) is activated. When increased blood pressure is sensed in the upper body, the parasympathetic nervous system (depressor response) is activated.
The sympathetic nervous system raises blood pressure by increasing its dynamic component. The dynamic component of blood pressure is related to heart rate, stroke volume, and total peripheral resistance. Elevated heart rate and stroke volume both cause blood pressure to increase by raising the volume and pressure of blood injected into the arterial system. Total peripheral resistance is increased when arterial smooth muscle constricts and thereby reduces the circulating arterial blood volume space.
Although very effective in compensating for upper body hypotension, the baroreceptor reflex takes time, on the order of 6 to 9 seconds, with heart-level blood pressure restored in 10 to 15 seconds (7). This compensatory response is therefore slower than the cerebral hypoxia reserve time of 4 to 6 seconds. If sufficient +Gz is experienced, the sympathetic response is inadequate and cerebral hypoxia occurs. A measure of autonomic nervous system response to +Gz is heart rate, which increases directly with increased +Gz level, reaching a maximum within a few seconds of exposure. High-sustained +Gz exposures usually result in a maximum heart rate of approximately 170 beats/minute.
In contrast, the parasympathetic nervous system attempts to lower upper body blood pressure by decreasing heart rate, stroke volume, and total peripheral resistance. This general relaxing of myocardial and vascular tissues occurs quickly, in comparison to the sympathetic nervous system response, and can be fully developed within 2 to 4 seconds (8,9). During −Gz, heart rates fall dramatically: reductions of 50 beats/minute have been recorded during exposures of −3 Gz with some subjects experiencing brief periods of asystole (10).
Adequate cardiac output depends on the supply of blood to the heart through venous return. Although the fluid model might predict that venous return is diminished during increased +Gz, early experiments determined that the abdominal contents (as a whole) behave like an enclosed fluid, and that venous return is generally maintained (7).
In addition to the baroreceptor response, sympathetic nervous system dominance is facilitated by the endocrine system. Physiological responses to air combat, aerobatics, centrifuge experiments, or any unusual G-exposure elicit an immediate “fight or flight” response with increased levels of epinephrine, norepinephrine, and serum cortisol (11). The endocrine response is slower than the baroreceptor reflex, but becomes important as G exposures increase in duration.
The respiratory system is also affected by increased +Gz. As hydrostatic pressures increase during increased +Gz, lung perfusion is redistributed toward the base of the lung, especially at relatively low G levels. During acceleration, the alveolae, owing to the vast differential in specific density between blood and air, expand at the top of the lung while those at the base of the lung, where most blood has moved, become smaller with some collapsing (12). As a result, ventilation/perfusion mismatch and acceleration atelectasis can occur. These responses are further described in Chapter 2.
Increased abdominal pressure during +Gz also prevents full descent of the diaphragm. This impairs vital capacity because of a reduced inspiratory capacity (12). Lung compliance decreases and results in an increased resistance to changes in volume. Reduced compliance and increased weight of the chest wall structures increase the work of respiration in proportion to increased +Gz. A total increase of 55% in the work of breathing occurs at +3 Gz. Further details are provided in Chapter 2.
At one time, aerospace physiologists were concerned that human exposures to greater than +9 Gz could lead to lung tissue injury. These fears have been proved unfounded, at least up to +12 Gz (13). Former concerns about poor blood oxygenation also proved unfounded, possibly because the major physiologic demands during exposure to G are anaerobic, with physiologic limitations caused by fatigue.
Symptoms and Signs of Uncompensated +Gz Stress
Visual
As +Gz increases, the first symptoms experienced usually consist of visual changes. The interior of the eye is enclosed and normally has an internal pressure of 10 to 21 mm Hg. The retinal artery pierces the posterior globe and enters the central retina with the optic nerve. For retinal blood perfusion to occur, arterial pressure must be greater than the internal eye pressure. If it is not, retinal ischemia occurs, first at vessels farthest from the optic disc and then with progression toward the central retina.
A pilot in flight who is exposed to increasing +Gz can experience dimming of vision, starting at the visual periphery. This is termed tunnel vision and is familiar to most pilots who have been trained to expect it. In the presence of continued (and increased) +Gz, visual symptoms can progress inward from the periphery to include the central vision, a symptom known as gray-out. Not all air crew experience loss of peripheral vision before central vision. If +Gz is reduced, restoration of vision occurs quickly.
With continued or increased +Gz, visual symptoms can progress from gray-out to complete loss of vision, or “blackout” (not to be confused with loss of consciousness). Brain and auditory functions remain undisturbed if there is no further decrease in brain-level blood pressure. Recovery from blackout occurs quickly on restoration of blood pressure. The presence of conscious function in the absence of vision can furnish pilots with a valuable warning that loss of consciousness is imminent unless appropriate steps are taken. Because of the repeatability of these symptoms, research studies often rely on subject reports of visual impairment as a measure of tolerance to +Gz.
Almost Loss of Consciousness
With increasing +Gz, symptoms of early cognitive impairment can develop. This syndrome, termed almost loss of consciousness (A-LOC), consists of a transient incapacitation without complete loss of consciousness that often occurs during and after relatively short-duration, rapid-onset +Gz pulses. A-LOC is characterized by a blank facial expression, twitching, hearing loss, transient paralysis, amnesia, poor word formation, and disorientation (14). The most prevalent symptom is reported to be a disconnection between cognition and the ability to act. The duration of incapacitation is much shorter than with G-induced loss of consciousness (G-LOC), reflecting a more transient degree of brain cell ischemia.
G-Induced Loss of Consciousness
If cerebral hypotension progresses beyond the symptoms of visual impairment and A-LOC, G-LOC can occur. G-LOC has been defined as a “state of altered perception wherein (one’s) awareness of reality is absent as a result of sudden, critical reduction of cerebral blood circulation caused by increased G force.” (15) Centrifuge subjects who experience G-LOC frequently appear to stare blankly before relaxing voluntary muscular control and exhibiting signs of loss of consciousness. Myoclonal jerking is often seen (approximately 70%), semipurposeful grasping and apparent efforts at reorientation are made, and amnesia is sometimes present with a complete unawareness that the event occurred. Following recovery from G-LOC, some subjects (and pilots in flight) have reported “dreamlets” that are similar to sleep dreams, except that they are of very short duration.
G-LOC incapacitation (after reduction of +Gz) has been divided into two periods: absolute incapacitation (or unconsciousness) and relative incapacitation. According to centrifuge studies, the average absolute incapacitation period lasts 12 seconds (range of 2 to 38 seconds). This is followed by a period of relative incapacitation consisting of confusion/disorientation that lasts an average of 15 seconds (range of 2 to 97 seconds). A pilot is unable to maintain aircraft control during either of these periods, the sum of which is the total incapacitation period, averaging 28 seconds (range of 9 to 110 seconds). There is apparently no permanent residual pathological effect from an uncomplicated G-LOC.
If rates of onset of +Gz are high, G-LOC can occur before other symptoms, including visual manifestations. Under these conditions, G-LOC can be rapid and lethal because it develops without warning. An example of this was documented several years ago through recovered telemetry data from a CF-18 Hornet jet aircraft. During an exercise combat engagement involving another aircraft, the pilot rapidly loaded the aircraft to +6.4 Gz, then lost control within 4 seconds. The aircraft entered a near-vertical dive and crashed. The data indicated that 18 seconds after the loss of control an attempted recovery was made. The data demonstrated a total period of incapacitation of 18 seconds. The pilot was then able to recognize his situation and attempt recovery—unfortunately too late. Figure 4-9 is a plot of the recorded data.
Human Tolerance to Sustained +Gz
Human tolerance to +Gz has been studied on ground-based centrifuges using human volunteers. Objective measures of tolerance in the past have included ear pulse opacity, direct and indirect measures of blood pressure, and loss of consciousness. A less objective, but more widely used measure, consists of subject reports of visual changes. Unfortunately, reporting is variable and may be influenced by psychological or social pressures, anatomy, and slowed mental processing.
Human tolerance to +Gz is influenced by many variables, including anthropometry (heart-to-brain distance), muscle straining, anti-G suit inflation, and rate of +Gz onset. To control against some of these factors, standardized
approaches have been developed. One is to determine the tolerance of relaxed subjects. This allows for +Gz tolerance to be reported without the confounding influences of muscle strain or anti-G suit inflation, and offers a means of determining passive psychophysiological compensatory responses. Slower G-onset levels allow for cardiovascular compensation to influence the measure. Faster G-onset levels measure tolerance before a full cardiovascular response occurs.
approaches have been developed. One is to determine the tolerance of relaxed subjects. This allows for +Gz tolerance to be reported without the confounding influences of muscle strain or anti-G suit inflation, and offers a means of determining passive psychophysiological compensatory responses. Slower G-onset levels allow for cardiovascular compensation to influence the measure. Faster G-onset levels measure tolerance before a full cardiovascular response occurs.
 FIGURE 4-9 CF-18 Hornet crash data. These data were recorded during the fatal crash of a CF-18 Hornet. Gz is depicted along the vertical axis whereas time (in seconds) is depicted on the horizontal axis. The plot demonstrates approximately 8 seconds of relative −Gz, followed by rapid onset to +6.4 Gz and G-LOC and loss of control. The next control input was made approximately 18 seconds later with a rapid onset increase to +7.4 Gz, too late to avoid the crash. |
In general, two separate types of subject tests are used, as defined by G-onset rate: (i) rapid-onset rate (ROR) tests and (ii) gradual-onset rate (GOR) tests. ROR is defined as a rate greater than 0.33 G/s, often as high as 6 G/s. GOR is defined as slower than 0.25 G/s. Measurements of relaxed ROR +Gz tolerance are approximately 1 G lower than GOR tolerances. The results of a study involving 1,000 relaxed male subjects reported tolerances presented in Table 4-2A (16). The results of World War II era centrifuge studies, based on subjective reports with onset rates of 2 G/s, are also presented in Table 4-2B (17).
Researchers have studied other potential influences on human tolerance to +Gz. Studies assessing female relaxed tolerance to +Gz concluded that they are equivalent to males, with reported ROR tolerances of 4.2 ± 0.5 G and GOR tolerances of 5.2 ± 0.6 G (18). Female time-to-fatigue during simulated air combat maneuvers is not significantly different from that for males (19,20). Menstruation in women on oral contraception has no effect on +Gz tolerance (19). Motion sickness lowers +Gz tolerance (21).
TABLE 4-2A | ||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||||||||||||||||
Relative Negative Vertical Acceleration and Negative Acceleration (−Gz)
In response to increased relative −Gz, heart rate is reduced and generalized vasodilatation occurs, a response that is relatively rapid. This response is dose related in the sense that increased relative −Gz, moving toward zero-G and then −Gz, results in increasing blood pressure in the upper body and a more vigorous parasympathetic response (10).
During −Gz, intracerebral blood pressure increases. Congestion of the face and a subjective sensation of eye bulging occurs; this can become intense with increasing −Gz. There is upward movement of the abdominal contents and
the work of breathing is increased. Inverted flight (−1 Gz) can be unpleasant, but tolerable. Between −2 and −3 Gz, there is severe facial congestion and occasional reddening of vision. Most subjects can tolerate −3 Gz for 5 seconds, although some can reach −5 Gz without injury (10,22). The feeling of facial congestion becomes intense at −3 to −4.5 Gz. The restraints, which are supporting the entire mass of the body, cause additional painful sensations. Competitive aerobatic pilots describe sustaining up to −9 Gz for very brief durations.
the work of breathing is increased. Inverted flight (−1 Gz) can be unpleasant, but tolerable. Between −2 and −3 Gz, there is severe facial congestion and occasional reddening of vision. Most subjects can tolerate −3 Gz for 5 seconds, although some can reach −5 Gz without injury (10,22). The feeling of facial congestion becomes intense at −3 to −4.5 Gz. The restraints, which are supporting the entire mass of the body, cause additional painful sensations. Competitive aerobatic pilots describe sustaining up to −9 Gz for very brief durations.
TABLE 4-2B | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| |||||||||||||||||||||
Some of the adverse effects of −Gz derive from increased arterial blood pressure in the head, especially where it is unopposed. Within the skull, where increased arterial pressures are balanced by increased pressures in the surrounding cerebrospinal fluid, adverse effects are generally not seen (23). Where increased pressures are unopposed, injury can occur. Facial petechiae have been described by competitive airshow pilots. Nose bleeds and subconjunctival hemorrhage have been reported due to high −Gz.
There are no generally accepted countermeasures to −Gz, although some aerobatic pilots report that they relax while exposed to −Gz so as not to further increase thoracic pressure.
The Push-Pull Effect
Related posts:
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
