Category/year
1960
1970
1980
1990
2000
2009
2010
2012
2013
National health expenditures, in billions
$27.4
$74.9
$255.8
$724.3
$1378.0
$2505.8
$2604.1
$2817.3
$2919.1
National health expenditures as percent of GDP
5.0
7.0
8.9
12.1
13.4
17.4
17.4
17.4
17.4
National health expenditures per capita
$147
$356
$1110
$2855
$4881
$8175
$8428
$8996
$9255
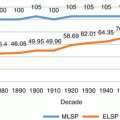
For decades, the growth rate of healthcare spending has exceeded the growth rate of the GDP. Thus, healthcare costs increased as a percentage of total national spending. For example, as GDP grew by 7.1 % in 1970, the national health expenditures grew by 10.6 %; and this trend only slowed down in 2009–2013, with growth rates slightly below to slightly above the overall GDP growth rate, as shown in Table 9.2.
Table 9.2
Average annual percent change from previous year in GDP and health expenditures
Category/year | 1970 | 1980 | 1990 | 2000 | 2009 | 2010 | 2012 | 2013 |
|---|---|---|---|---|---|---|---|---|
GDP | 7.1 | 10.3 | 7.6 | 5.6 | 3.8 | 3.8 | 3.9 | 3.7 |
National health expenditures | 10.6 | 13.1 | 11.0 | 6.6 | 6.9 | 3.9 | 4.0 | 3.6 |
National health expenditures per capita | 9.2 | 12.0 | 9.9 | 5.5 | 5.9 | 3.1 | 3.3 | 2.9 |
This trend indicates a cause for concern. It is clear that healthcare spending has grown considerably over the past 50 years, at a rate much higher than the average for all other spending. At the same time, the slowdown in the last 5 years also indicates that we may have reached a steady state in healthcare expenditure dynamics. The recent slowdown in healthcare inflation may also be just a temporary phenomenon, explained by the recession and the loss of healthcare coverage by the unemployed workers. However, we also suspect that the Patient Protection and Affordable Care Act (PPACA) of 2010, commonly known as Obamacare, may have contributed to a more permanent reduction in healthcare inflation through its focus on expanding coverage and curbing costs.
Even if the healthcare spending is stabilized at approximately 17.4 % (or a little more than one-sixth) of US GDP (and that is an assumption that remains to be tested by future data), this level of spending by far exceeds comparable spending of other industrialized nations. Canada, for example, spent only 10.2 % of its GDP on healthcare in 2013 (and appears to have spent only 10 % in 2014); Germany spent 11.0 %; Japan – a country with a much older population than the United States – spent 10.2 %; the United Kingdom, 8.5 %; and France, 10.9 % (OECD 2015).2 The average for healthcare spending for all nations that belong to OECD, a group that generally includes some of the most industrialized and prosperous countries in the world, is 8.9 % of GDP. The United States spends approximately 80 % more than average on healthcare and almost 50 % more than the second-highest spender in the OECD group, the Netherlands.
Are we paying more for exceptional health outcomes? Unfortunately, this does not appear to be the case. The United States underperforms in some of the most common measurements of health outcomes, such as life expectancy at birth (a child born in the United States in 2013 could expect to live to 78.8 years of age on average, as compared to Canada’s 81.5 years, France’s 82.3 years, Japan’s 83.4 years, and the OECD average of 80.5) and infant mortality rate (6.0 deaths per 1,000 live births in 2012, as compared to Canada’s 4.8, France’s 3.6, Japan’s 2.1, and the OECD average of 4.1) (OECD 2015).
9.2.3 Allocation of Resources in Society and the Role of Markets; Healthcare Markets as a Special Case
Economists posit that certain structures and institutions contribute considerably to the most efficient use of resources. For example, economists consider markets to be one of the best ways to achieve optimal allocation of resources, with buyers and sellers coming together to determine an equilibrium price for goods and services traded in the markets with little to no outside interference. The price is established at the level where the quantity demanded is exactly equal to the quantity supplied, and price will fluctuate according to the changes in factors that influence demand or supply. If the sellers make profits that are higher than the average in other marketplaces, more providers will enter the market and drive the price down; if the sellers’ profits are lower than average or if they lose money, they will exit the market, and the price will go up.
Efficient marketplaces, however, require certain conditions to exist. First, the rules of the game, such as the structure for assuring property rights and efficient trading mechanisms must be in place, so that both the seller and the buyer can engage in transactions freely, without fear of loss of their property yet with little undue interference that creates artificial barriers to the market functioning. Second, both the seller and the buyer must have the same level of knowledge about the characteristics of goods or services being traded; this condition is known as symmetrical information. Third, competition must exist on both sides, as unregulated marketplaces with one or few sellers (or one or few buyers, for that matter) will result in artificially high (or in some cases, artificially low) prices and inefficient transfer of resources from one marketplace participant to another. Finally, decisions made by economic actors should not impact third parties. In other words, one’s decision to take an action should not impose a cost or confer a benefit on anyone else but oneself.
How different are the healthcare markets from the marketplace described above? In one word: considerably. First, healthcare providers are heavily regulated by multiple agencies on the federal, state, and local levels, with some private and quasiprivate regulators and organizations involved in the process (such as The Joint Commission, or JCAHO). Field notes that such oversight is widely acknowledged as necessary, since human lives are at stake. The debates, however, revolve around the optimal way of structuring the regulations and the regulating agencies, which often operate without coordination, and may create a regulatory maze for bringing new treatments to the market (Field 2008).
Second, the providers and the patients have vastly different knowledge available to them, as described in the later part of this chapter – which can be an even greater issue in the markets for health insurance.
Third, local markets for healthcare tend to be dominated by large networks of healthcare providers and large insurance companies. Federal and state governments and agencies are also some of the largest buyers and providers of healthcare and related services.
Finally, decisions that individuals make have an impact on the rest of us: the uninsured transfer costs of their treatment onto providers and insured individuals; those receiving flu vaccinations provide a benefit to the rest of the society by reducing the risk of their getting sick; and perhaps most importantly, insurance reduces or eliminates the incentive to shop for better healthcare prices by transferring the cost of treatment to someone else.
Thus, healthcare markets are complex and tend to be less than fully efficient. They function differently from typical markets. The tools of economic analysis can still assist healthcare practitioners, administrators, and policy makers to navigate such complex markets with greater efficiency.
9.3 Cost-Benefit Analysis
9.3.1 The Cost-Benefit (CBA) Approach
Cost-benefit analysis (CBA) is perhaps one of the best-known and most-used tools in economics, public policy, and business. In fact, the US government has since 1981 required all new federal regulations to undergo the cost-benefit analysis process to demonstrate their value to the taxpayers.
The approach sounds simple: we compare the costs and the benefits of various choices, and choose the one that maximizes the difference between benefits (B) and costs (C), discarding those where such difference (B-C) produces a negative result. The difference on its own represents an absolute value. To improve this analysis even more, we may simply take the ratio of benefits to costs (B/C); discard those choices resulting in a ratio of less than 1; and select the choice with the highest benefit-to-cost ratio from the remainder.
9.3.2 Assigning Monetary Values to Benefits and Costs of Treatment
In practice, however, cost-benefit analysis tends to be complicated. The nature of the cost-benefit analysis requires us to compute both costs and benefits in the same unit of measurement (e.g., dollars). The costs are easily tallied in dollars, but the benefits are normally made through gains in health outcomes. Such nonmonetary benefits, which may include gains in life years or in quality of life, will then require translation into a monetary equivalent.
How do we value a life then? This question is morally distasteful to many. However, economists and policymakers would argue that the decisions people make and the policies we develop both at national (macro) and organization/individual (micro) levels actually require us to engage in some level of valuation of a human life. More importantly, these studies of the value of statistical life (VSL) also allow us to engage in marginal analysis of costs of reduction of risks to human lives. Table 9.3 summarizes some of the major approaches to valuation of life for the purpose of CBA.
Table 9.3
Selected approaches to life valuation
Approach | Description |
|---|---|
Human capital/wage-based valuation | This methodology assigns a value to human life based on expected economic productivity of an individual. Not surprisingly, lives of highly educated and professionally successful individuals earning high wages will be valued very highly, while the lives of those of retirement age will be valued lower. |
Willingness to pay | Estimated through studying decisions in which individuals demonstrate willingness to pay for reducing risks to their life. For example, if an individual is willing to pay $1000 for a medical procedure that reduces the risk of death by 0.01 %, that decision places a valuation of $1000/0.01 % = $10 million. |
Willingness to accept | Estimated through studying the individuals’ willingness to accept situations associated with higher risks to life and health for a certain premium, such as high-risk occupations (firefighters, policemen, etc.). Many US government agencies use the method of compensating wage differentials (wage premiums associated with risks of fatal injuries in the workplace) as the method for estimating the value of mortality risk reduction (Cropper et al. 2011). |
Stated preferences/contingent valuation | In this approach, the researcher poses hypothetical questions about premiums the individual is willing to pay for various reductions in risk to their life, and collects individual’s stated preference for analysis. |
Cropper and colleagues, in summarizing the results of multiple meta-analyses of US hedonic wage studies conducted over 1974–2002 and normalized to $2009, noted estimates of valuation of statistical life (VSL) that ranged from $2.0 million to $11.1 million (Cropper et al. 2011). For stated preference/contingent valuations studies, estimates ranged from $2.7 to $8.5 million. Thus, valuations in the middle of this range would be considered reasonable by most economists.
9.3.3 Intertemporal Nature of Costs and Benefits
We encounter a disconnect in timing between incurring costs and receiving benefits of a decision, when costs are incurred now (cost of providing treatment, which may include cost of chemotherapy, surgery, hospital stay, ambulatory care, follow-up care, medication, possible lost wages, pain and suffering associated with undergoing invasive treatment, and other direct and indirect opportunity costs) but benefits are derived in the future over many years (such as improved quality of life, extended life expectancy, higher productivity, and higher wages through lower absenteeism in the workplace).
Future costs and benefits are also not certain. They represent our best estimate as to what may happen in the future. This will require us to engage in the discounting of future costs and/or benefits to the present day, thus making decisions about the appropriate discount rate to be used in the present value formula:
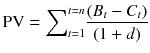In this formula, B t is the benefit derived in time period t; C t is the cost incurred in time period t; and d denotes the discount rate applied to the future benefits and costs over n time periods. Clearly, the higher the discount rate, which may be driven by the higher uncertainty of a benefit, the lower the net present value of future benefits and future costs of a choice.
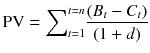
Cost-benefit analysis may be used to evaluate a single choice or multiple choices. Most of us perform a version of cost-benefit analysis in our minds on a daily basis without realizing it when making decisions that involve choices.
9.3.4 Cost-Effectiveness Analysis (CEA)
Cost-effectiveness analysis (CEA) attempts to establish a specific performance threshold for benefits to be achieved by a project or medical intervention, and similar to the CBA methodology, CEA measures the total direct and indirect costs of attaining such a goal. To eliminate the issue of converting benefits to monetary values, the benefit goals are expressed in nonmonetary terms, such as achievement of a specific live expectancy for the population, number of lives saved, or reduction of incidence of disease in population. The change in costs is then compared to the change in performance in the metric of interest to obtain a CEA ratio, and the projects are prioritized based on their ratios.
9.3.5 Quality Adjusted Life Year
The cost-utility analysis (CUA) is a special case of the CEA approach, and is utilized extensively in healthcare. Prior to jumping into the discussion of the methodology of cost-utility analysis, it will be useful to review the concept of quality adjusted life year (QALY). QALY is a measure of health improvement widely used in assessing cost-effectiveness of therapies both in the United States and the United Kingdom, and thus, in making decisions about efficient allocation of scarce resources in healthcare interventions (known as productive efficiency). QALY allows us to recognize that quality of life matters greatly in the assessment of efficiency of treatments; and that gaining a year of life that is fully functional and allows the individual the full freedom of productive and leisure activities and free of pain and suffering is much more valuable than gaining a year of life confined to a bed and spent in constant pain.
The basic approach of QALY is to recognize a scale of health states that range from zero to one, where zero corresponds to being dead, and one corresponds to being in perfect health. The other health states can be rated as between zero and one. In rare circumstances, it is possible to rate a state of health as a negative QALY value (i.e., worse than the state of death), thus subtracting from total QALYs accumulated over period studied. QALY scales are constructed in such a way that they can be aggregated for analysis (Weinstein et al. 2009).
For example, when comparing two cancer interventions which result in an average gain of 2.0 years (Intervention A) and 3.0 years (Intervention B) of life expectancy for intervention recipients, we may be tempted to identify Intervention B as a superior choice. However, if Intervention A results in an aggregate QALY gain that exceeds that of Intervention B through allowing the patient higher quality of life and better state of health, we may argue Intervention A to be a better choice from a utilitarian point of view, and likely, from a point of view of many patients as well.
The QALY approach has its limitations as well, and has attracted its share of criticism. First, QALY health state valuations are those of policy makers, and not those of people on whose behalf decisions are being made (and who may not be fully able to assess the implications of the state of health if they are not currently in that state of health). Second, QALY computations by their design imply that the value of an intervention is proportional to the recipient’s capacity to benefit (Nord et al. 2009). For instance, younger patients who may gain more years of life at higher QALY rating from a treatment will be favored over older patients, thus raising concerns about societal equity issues. Another concern yet is that chronic conditions, such as cancer, will be discounted in favor of prevention of fatal accidents in people with normal health (ibid).
There is also some disagreement on whether QALY is an appropriate measure for evaluating health states for individuals receiving end-of-life care. Round (2012) notes that the arguments typically advanced against using the QALY approach include: lack of expected survival gain from an intervention and thus inappropriateness of a time-based measure such as QALY; priority of other dimensions of quality of life over health status; measure that uses death as an anchor point invalid when death is imminent; unstable patient preferences and time valuation at the end of life; and disconnect between cost-effectiveness and desirability of certain treatments. Round (2012) argues that while such arguments have some weight, there is still no acceptable robust alternative to QALY that can be used for policy- and decision-making in valuing and assessing the health states of those receiving end-of-life care, and using such data for allocating appropriate resources.
9.3.6 The Cost-Utility Analysis Approach
Cost-utility analysis (CUA) is an alternative approach to cost-benefit analysis, which does not require conversion of benefits derived from medical intervention into dollars, and thus allows us to avoid the often difficult and controversial exercise of computing the value of statistical life or value of incremental gains in life. Rather, cost-utility analysis measures the costs of gains in QALYs made in various healthcare interventions, and considers the total costs and the cost per QALY gained.
By way of illustration, when engaging in CUA, we may compare two cancer interventions that on average result in gains of 2.3 and 2.5 quality adjusted life years, and cost $20,000 and $2,000,000, respectively. Intervention A is somewhat less effective in terms of total QALYs gained (8 % less effective, as measured in QALYs), but it costs much less than Intervention B. Intervention A’s cost is $8696 per QALY and Intervention B’s cost is $800,000 per QALY gained. The gain in the life expectancy needs to be balanced against the cost-utility analysis issues identified.
9.3.7 Other Approaches to Economic Evaluation of End-of-Life Care and Experiences
All three economic evaluation approaches identified above (cost-benefit analysis, cost-effectiveness analysis, and cost-utility analysis that incorporate QALY as a measure of outcomes) may generally be used in evaluating end-of-life care. In recent years, however, additional research targeting economic evaluation of such care has emerged that offers additional perspectives to be considered.
Coast notes there are “three broad normative theoretical bases that economists are likely to choose from: welfarism, narrow extra-welfarism interpreted as health maximization or an alternative extra-welfarist perspective focusing on opportunity for a good death,” and offers the extrawelfarist capability approach as a starting point for thinking about economic analysis of end-of-life care (Coast 2014). The capability approach, based on the work by the Nobel Laureate Amartya Sen, evaluates interventions based on their impact to the individual’s “capability well-being,” or what the individual is capable of doing rather than what the individual chooses to do with their life. Such an approach, Coast argues, allows us to analyze quality of life and quality of death to the dying individual and their family and friends.
Related posts:
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
