16 Corrado Priami and Melissa J Morine Department of Mathematics, University of Trento, and The Microsoft Research–University of Trento Centre for Computational and Systems Biology Technological advancements in the past decade have opened up vast avenues for systems-level understanding of nutritional health. In a field that developed from studies focusing on single nutrients and single genes, it is now commonplace in molecular nutrition to generate data sets containing tens of thousands, or even millions, of variables in a single assay. Although data analytical methods have progressed in the last decade, they have generally not followed the same pace as the technology for data generation. In particular, network analytical approaches have been mainly developed blindly with respect to the biological content of the available data. Indeed, some of the very same network analysis approaches have been proposed for molecular systems as well as social networks, for resource distribution networks as well as markets, simply because all these phenomena can be represented by graphs. A classic example is the search for hubs in networks by exploiting the topological features of the graphs. Although hubs are important, the functional meaning of graph elements might not always be related to topological characteristics. A major challenge for systems nutrition (SN) is in processing, analysis and interpretation of the growing body of available data by incorporating in the methods the idiosyncrasies of the biological systems of interest. SN and bioinformatics – which lie at the intersection of molecular biology, mathematics, engineering and computer science – comprise methods ranging from dynamic simulation to analysis of high-throughput (i.e. omic) data, with the goal of understanding nutrition-related systems at the molecular level (De Graaf et al. 2009). In this chapter we review the prevailing methods and achievements in bioinformatics and systems biology that have driven research in SN. Gene set analysis has arguably become the most widely adopted method for high-throughput gene expression (i.e. transcriptomic) analysis. The general premise of gene set analysis (GSA) is to assign the genes in a high-throughput data set to functional categories, and then to test each category as a whole for significant differential expression. By abstracting gene-level information to the level of biological process, GSA has advantages both in terms of statistical power (by dramatically reducing the burden of multiple testing) and biological interpretability. The most commonly used functional categories (i.e. gene sets) are metabolic/signalling/regulatory pathways or Gene Ontology terms; however, in principle any functional grouping could be used. Other examples of gene sets that have been successfully applied in this context include cytobands, genes regulated by common microRNA (miRNA)/transcription factors, and pre-defined groups of disease genes, among others. The common goal of any GSA algorithm is to identify coordinated changes in sets of functionally cohesive genes (defined a priori). However, there is a range of algorithms that have been developed for this purpose, and an even wider range of implementations available through standalone software, libraries for programming languages such as R or python, or via webservers (for an extensive list of tools see http://bioinformatics.ca/links_directory/category/expression/gene-set-analysis). The bioinformatics community has been so active in developing methods for GSA over the past 10 years that it has become a challenge simply to select the preferred method for use in analysis of a given data set. A 2009 survey by Huang et al. (2009a) identified 68 unique tools for GSA, and this number has only grown since then. Understanding and categorising the many GSA tools are challenging for end-users, and this may even be an obstacle for bioinformatics groups aiming to develop new approaches without replicating existing methods. There are, however, a smaller number of tools that tend to dominate the field, such as updated versions of the GSA algorithm proposed by Mootha et al. (2003; Subramanian et al. 2005), as well as the DAVID tool (Huang et al. 2009b), BiNGO (Maere et al. 2005), GoMiner (Zeeberg et al. 2003) and FatiGO (Al-Shahrour et al. 2004). Despite the breadth of approaches to GSA, most methods can be broadly categorised as those based on over-representation; expression change scoring; or pathway topology. For an extended review of these approaches see Khatri et al. (2012). Over-representation (OR) methods are the earliest examples of GSA. They are also arguably the simplest, and most broadly applicable across technological platforms. The general approach to OR proceeds as follows: first, a list of significantly regulated genes is determined from the microarray data using t-test, linear regression and so on, at a defined significance threshold. Next, the number of significant genes is counted both in the background list (often the entire microarray) and in each pre-defined gene set. Finally, each gene set is tested for significant enrichment with the genes of interest, typically using a test such as Fisher’s exact, hypergeometric, chi-square or binomial. The strength of the OR enrichment approach is in its simplicity. Using only a list of significant genes as input (without the need for fold change values or other quantitative measurements), this approach can be easily applied across a range of technological platforms, such as microarray, ChIP-on-chip, SNP array and so on. However, this simple use of gene lists also implies that OR approaches consider highly significant genes as identical to marginally significant genes, thus ignoring a potentially informative dimension of the data. Furthermore, the use of a significance threshold to define the initial gene list may exclude potentially informative genes that miss this threshold. Although there are relatively widely accepted standards for p-value thresholds in transcriptomic analysis, gene lists are often chosen also on the basis of fold change, for which there are fewer standards and which may or may not reflect true biological importance. Expression change scoring (ECS) approaches inherently consider expression data in the calculation of gene set enrichment, and do not impose pre-selection of a significant gene list. The best-known example of an ECS approach was proposed by Subramanian et al. (who coined the initialism GSEA, for gene set enrichment analysis), with the original methodology paper receiving over 4000 citations to date (Subramanian et al. 2005). Similar to OR methods, ECS approaches to GSA begin with calculation of differential expression scores for each gene in the data set. These raw gene-level statistics may be used, or they may be transformed using absolute values, square root or rank statistics to remove the distinction between up- and downregulated genes (Subramanian et al. 2005; Saxena et al. 2006; Morine et al. 2010). These gene-level scores are then aggregated to gene set–level statistics, and the significance of each gene set is typically determined by a permutation test, either permuting the class labels or the gene labels. One drawback of OR and ECS approaches, when applied to pathway gene sets, is that they do not consider the connectivity patterns between genes in each pathway. To illustrate the relevance of this information, consider the case of a very large pathway for which gene expression data have been measured across two conditions. It may be the case that the condition-specific expression changes in the pathway are localised to one small subregion, or alternatively they may be distributed evenly throughout the pathway. Pathway topology (PT)-based approaches were developed in an effort to capture this information in GSA. Current implementations use an ECS or OR approach to determine gene-level changes, then combine this statistic with gene–gene expression correlations (or a similar statistic) within the pathway (Rahnenführer et al. 2004; Tarca et al. 2009). The clear advantage of this approach is that it explicitly models pathway connectivity structure, which is a step closer to an understanding of dynamic system behaviour. However, it should be noted that the precise connectivity structure for many pathways is still only partially known, particularly when considering tissue- and cell type–specific activity. In the case of OR, ECS and PT approaches, the typical outcome of GSA is a list of gene sets that are significantly responsive to a perturbation or correlated with a particular phenotype. Depending on the database of gene sets used, this list of significant gene sets can become very long, containing hundreds or even thousands of gene sets. In this case, the problem of the lack of interpretability of high-throughput data is not resolved, only reduced. Furthermore, the list of significant gene sets often contains redundancies in terms of gene content (for instance, in the case of multiple related signalling pathways with a core set of shared genes). For this reason, a number of tools and approaches have been developed to aid in the interpretation and prioritisation of GSA results. One such method, developed by Alexa et al. (2006) for the use of Gene Ontology (GO) terms as gene sets, involves explicit consideration of the GO structure in calculating GSA p-values for GO terms. The GO database is a controlled vocabulary for representing biological processes, functions and cellular compartments. It is structured as a directed acyclic graph, wherein the lower (child) nodes represent more specific biological categories, and each node inherits the categories of its parents. The entire collection thus appears as a hierarchy with a strong dependency structure between the nodes, in the sense that the majority of genes in a given child node will also be found in its parent node. Because of this dependency structure, any assumption of independence of gene sets is not valid. The methods proposed by Alexa et al. (2006) address this lack of independence in two ways. The first approach (called elim) examines the GO hierarchy from the bottom up, testing each GO term for significant enrichment with the given list of significant genes, then removing those genes from the parent terms if the tested child term is significantly enriched (essentially decorrelating the hierarchy). This approach favours the more specific child terms, which implicitly improves the interpretability of the results, as higher-level parent terms can become very broad in scope. In the second approach (called weight), significance scores of parent/child term pairs are compared, and the genes in the less significant term are downweighted. Although this second approach does not decorrelate the hierarchy, it enables local prioritisation among strongly dependent term pairs. Another method for the interpretation and prioritisation of gene sets is called the leading-edge approach (Subramanian et al. 2007), which identifies gene sets containing the most highly scoring genes (i.e. the leading-edge subset). The implementation of this method allows for heatmap visualisation and calculation of correlation coefficients to assess the similarity between gene sets containing members of the leading-edge subset. Similar in concept to the approach of visualising the overlap between gene sets, the clueGO plugin (Bindea et al. 2009) for Cytoscape implements an OR approach to GSA and produces a network of enriched KEGG pathways of GO categories, wherein weighted links between gene sets represent the similarity between them, in terms of overlapping gene content. The approaches already presented are relatively straightforward for the interpretation of data from simple study designs focusing on, for instance, a single nutrient/drug challenge or controls versus cases of a Mendelian disease. It is often the case in nutrition, however, that a researcher may be interested in the effects of a particular nutrient on a particular disease, and the high-throughput molecular changes that mediate the two. This complicates the interpretation of GSA results, because the gene sets that are most responsive to the nutritional intervention may not be those that are most strongly linked to the disease of interest (Morine et al. 2010). Furthermore, complex study designs involving multiple doses, time points and batches complicate the process of calculating a single statistic for each gene, as required by ECS approaches. Data sets produced in nutritional genomics studies are often of very high dimension. Human expression microarray platforms typically measure 20 000+ genes (with some platforms measuring exon-specific expression) and human SNP arrays may produce genotype data for as many as 5 million loci. Similarly, next-generation sequencing platforms produce billions of base pairs of data, either representing the whole genome or the expressed subset (i.e. exome sequencing or RNAseq). Although proteomics and metabolomics platforms do not benefit from the same technical advantages of nucleotide-based platforms, these assays are constantly improving in sensitivity, producing data on thousands of proteins and metabolites. Clearly, each of these platforms offers a great opportunity for understanding nutritional processes with high precision, but the analysis and interpretation of these complex data structures have become a significant bottleneck in bioinformatics and systems biology (Palsson and Zengler 2010). The simplest approach to identifying variables in a high-throughput data set that correlate with, for instance, a given phenotype response variable is to perform serialised bivariate analysis (such as linear or logistic regression), comparing each variable in the omic dataset to the response variable. Although straightforward and easily interpretable, this approach does not capture the correlation structure within the data set. Multivariate analysis incorporates a range of approaches for exploring the structure within and between multivariate datasets. A common underlying theme across many multivariate techniques is dimensionality reduction – that is, identifying informative low-dimensional representations of high-dimensional datasets. Although not all methods for multivariate analysis are covered in this chapter, Table 16.1 describes an extended list of approaches. Table 16.1 Multivariate statistical approaches for analysis of high-throughput data. Cluster analysis is a widely used method for identifying groups of strongly correlated samples and/or variables in multivariate datasets. The most common methods for clustering methods, k-means and hierarchical clustering, are considered as unsupervised methods as they assume no prior knowledge of sample or variable classes. Hierarchical clustering does not assign observations to discrete clusters, but instead constructs a hierarchy of similarity, often visualised as a dendrogram. This can be achieved either through agglomerative clustering (identifying similar observations and building the hierarchy from the bottom up) or divisive clustering (starting with the complete data set, and successively dividing it into nested subfractions). In either case, a similarity metric is required to define the similarity between observations quantitatively. Common similarity metrics include Euclidean, Manhattan and Mahalanobis distance. Apart from the similarity metric, a linkage criterion is also required in order to define the distance between clusters of observations. This may be the distance between the closest two observations between two groups (single-linkage clustering); the farthest two observations (maximum linkage clustering); or the distance between the centroid of the two groups (average linkage clustering). Given the simplicity and speed of hierarchical clustering, it is generally worthwhile to apply multiple similarity and linkage metrics to examine the structure of the data fully and identify observations that may strongly influence the clustering result. Unlike hierarchical clustering, k-means clustering produces a discrete assignment of observations to clusters. The algorithm for k-means clustering generally proceeds by selecting k initial cluster centres and assigning each observation to the closest centre. Once each observation has been assigned, new cluster centres are calculated and each observation is assigned again to its closest cluster; in this step, some observations will change cluster while others will remain the same. The step of cluster centre calculation and observation reassignment is repeated until no observation changes cluster. In the application of k-means clustering, it is typical to run the algorithm across a range of values of k, and assess the goodness of fit of each result to the data using a diagnostic such as the elbow method, an information criterion method such as Akaike’s Information Criterion, or the Gaussian approach proposed by Hamerly and Elkan (2003). The best-known approach to dimensionality reduction is principal component analysis (PCA), first proposed by Karl Pearson (Pearson 1901), which identifies linear combinations of the variables in a multivariate data set that represent the variance structure in a smaller number of latent, orthogonal vectors. To illustrate with a simple example, consider a transcriptomic data set containing expression measurements for a large number of genes across a group of individuals. It may be the case that a subset of the genes displays strong correlation with each other, and thus could be represented by a composite (latent) variable that captures a large amount of the variance in these genes. The orthogonal transformation imposed by PCA is such that the first latent vector (first principal component) accounts for the largest amount of variability in the data set, with each successive component accounting for less variability and being uncorrelated to the rest (i.e. due to the orthogonality constraint). Plotting the samples in this low-dimensional space (on the first two principal components, for example) may reveal an informative grouping structure across the samples, such as grouping by dietary treatment, phenotype, gender and so on. As it is increasingly common to measure more than one omics data type on a given set of samples, methods for exploring correlation structure within and between two multivariate data sets are essential for efficient analysis and clear interpretation of these large data sets. Canonical correlation analysis (CCA), originally proposed by Hotelling (1936), uses a latent variable approach to identify low-dimensional correlations between two sets of continuous variables – that is, by identifying maximally correlated pairs of latent variables. CCA accepts as input two matrices, X of dimension n × p and Y of dimension n × q, both measured on the same n samples. The specific aim of CCA is to identify H pairs of loading vectors ah and bh of dimension p and q, respectively, that solve the objective function where h is the chosen dimension of the solution, and the n-dimensional latent variables Xah and Ybh denote the canonical variates. Analogous to PCA, the first dimension will represent the most strongly correlated canonical variates, with successive dimensions being progressively less correlated. Also similar to PCA, each pair of canonical variates is orthogonal to each other pair, which aids in the interpretability of CCA results as the variables represented on each dimension will be largely non-redundant (i.e. each dimension captures a unique subset of the data). A fundamental limitation of CCA when applied to cases where p+q>>n (as is the case with high-throughput data) is that the solution of the objective function requires calculation of the inverse of the covariance matrices XX′ and YY′, which are singular in the case of p+q>>n and thus lead to non-unique solutions of the canonical variates. Because of this, a number of authors have proposed methods for penalising the covariance matrices to allow for reliable matrix inversion. A penalised version of CCA using a combination of ridge regression (also known as Tikhonov regularisation) and lasso (least absolute shrinkage and selection operator) shrinkage (Tibshirani 1996) was proposed by Waaijenborg and Zwinderman (2009). Briefly, ridge regression obtains non-singular covariance matrices XX′ and YY′ by imposing a weighting penalty on the diagonal of the covariance matrices, wherein highly correlated pairs of variables receive similar weights. Lasso shrinkage imposes an additional penalty that shrinks variables with low explanatory power to zero, and thus can be viewed as a variable-selection procedure. Partial least squares (PLS) regression aims to model the relationship between two data sets in a regression context, where one data set is considered as a predictor and the other as a response (Wold et al. 1984). An example of where this could be appropriate in nutritional genomics is the analysis of multivariate dietary intake data (predictor) and transcriptomic data (response), as in Morine et al. (2011). As with CCA, PLS takes as input two matrices, X of dimension n×p and Y of dimension n×q. Although there are a number of variants of PLS, the general approach seeks a decomposition of X and Y with p– and q-dimensional loading vectors to optimise the objective function Note that the PLS algorithm seeks to maximise the covariance as opposed to correlation between the n-dimensional latent vectors, and performs the calculation based on the residual matrix Xh-1 as opposed to X, as with CCA. An attractive feature of PLS is that it does not require inversion of the covariance matrices and thus it can be applied in the case of p+q>>n. However, penalised versions of PLS have been proposed, using lasso or ridge in order to facilitate variable selection simultaneously with dimensionality reduction (Kim-Anh et al. 2008). In addition to variation in the algorithm for PLS objective function optimisation (with NIPALS and SIMPLS being the most common; Alin 2009), a number of extensions to PLS have been proposed to facilitate its applicability to various data forms, such as canonical mode PLS (Lê Cao et al. 2009) and PLS discriminant analysis (Lê Cao et al. 2011). Network inference complements the component-centric approach in which a gene or a protein of interest is fixed, and then local interactions with the selected gene or protein are identified by possibly fixing a distance for transitive interactions. Although this approach has been and still is very successful in identifying relevant pathways, it is time-consuming and needs lot of work and literature searching to produce new knowledge. Furthermore, it rarely identifies cross-talk between pathways and typically reflects the canonical pathways stored in the available databases. The environmental effects (mainly diet) on molecular processes are thus neglected, and high-throughput assays for observing thousands of variables simultaneously are not considered in these approaches. Complementing the component-centric approach with computational methods that explore omics data could lead to the identification of interaction networks that provide a comprehensive view of the biological processes of interest, including their interactions with the reference environment. A main issue in network inference is the validation of the outcome of the procedure. Indeed, the noise in the measurements and the stochastic nature of many biological processes (e.g. gene expression) make identification of the physical interactions very difficult. Algorithmic approaches to infer the network structure of large-scale, and often multi-omic, experimental data have recently emerged. The main algorithms are grouped into classifier-based and reverse engineering from steady-state and/or time-series data of perturbation experiments. We start by looking at classifier-based algorithms.
Data Analytical Methods for the Application of Systems Biology in Nutrition
16.1 Introduction
16.2 Gene set analysis
Statistical approaches to GSA
Interpretation of GSA results
16.3 Multivariate analysis
Method/References
Description
Data input
Cluster analysis
Denotes a set of related methods for identifying either discrete or hierarchical clusters of samples/variables
Multivariate matrix of p variables for n samples
Principal component analysis
Identifies linear combinations of variables in a multivariate data set to represent a maximal amount of variance along a smaller number of dimensions
Multivariate matrix of p variables for n samples
Factor analysis
Similar to principal component analysis, but focuses on the covariance among the variables rather than the variance
Multivariate matrix of p variables for n samples
Multidimensional scaling
Similar to principal component analysis, but aims to conserve interpoint distances in the high-dimensional space by minimising a loss function
Multivariate matrix of p variables for n samples
Linear discriminant analysis
Identifies a linear function representing a linear decision boundary between classes of observations
Multivariate matrix of p variables for n samples, and discrete class vector of length n
Support vector machine
Identifies a hyperplane representing the (possibly non-linear) decision boundary between classes of observations
Multivariate matrix of dimension n×p and discrete class vector of length n
Random forest
Generates a set of classification/regression trees based on sampling (with replacement) of variables within the predictor data set, to produce ensemble classifier rules and measures of relative variable importance
Multivariate predictor matrix of dimension n×p and discrete/continuous class vector of length n
Canonical correlation analysis
Identifies maximally correlated latent variables determined from linear combination of p and q variables measured across n samples
Two multivariate matrices of dimension n×p and n×q
Partial least squares regression
Identifies a regression model from a linear combination of p variables in X, in order to predict continuous response variable y (in the case of univariate response), or a linear combination of q variables in Y (in the case of multivariate response)
Multivariate predictor matrix of dimension n×p and continuous response matrix of dimension n×1 (univariate response) or n×q (multivariate response)
Partial least squares discriminant analysis
Same as partial least squares regression, but adapted to discrete response variables
Multivariate predictor matrix of dimension n×p and discrete response matrix of dimension n×1
Generalised canonical correlation analysis
Generalisation of canonical correlation analysis to model correlation structure across > 2 multivariate matrices
K multivariate matrices of dimension n×pk
Cluster analysis
Principal component analysis
Canonical correlation analysis
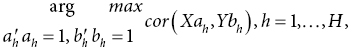
Partial least squares regression
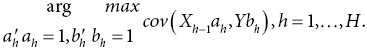
16.4 Network inference
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree