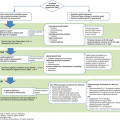
Good doctors use both individual clinical expertise and the best available external evidence, and neither alone is enough. Without clinical expertise, practice risks becoming tyrannized by evidence, for even excellent external evidence may be inapplicable to or inappropriate for an individual patient. Without current best evidence, practice risks becoming rapidly out of date, to the detriment of patients.
Sacket et al, 1996
Evidence-based medicine (EBM) is “the conscientious, explicit, and judicious use of current best evidence in making decisions about the care of individual patients.”1,2 The phrase evidence-based medicine was developed by a group of physicians at McMaster University in Hamilton, Ontario, in the early 1990s.1,3 EBM is a combination of clinical expertise and best evidence, as eloquently stated by Sacket and colleagues in the above quotation.1 The EBM definition has two basic components: the first is “the conscientious, explicit, and judicious use,” which, in trauma, applies to split-second decision in the face of an immense variety of unexpected clinical scenarios. The time pressure and the irreversibility of many surgical procedures enhance the anxiety of decision making.4
The second component of the EBM definition is “best evidence.” What constitutes “best evidence”? Best evidence is “clinically relevant research,”1 which can both invalidate previously accepted procedures or replace them with new methods that are more powerful, efficacious, safe, and cost containing.5 In simple words, it comes down to “How does the article I read today changes (or not) how I treat my patients tomorrow?”6
Searching for evidence usually starts with the formulation of a searchable clinical question. For this purpose, the PICO framework is very helpful.7 PICO stands for patient (P), intervention (I), comparator (C), and outcome (O). When searching for evidence, or determining whether the most recently read article applies to the patient in front of you, quickly define whether the PICO observed in the study are similar enough to allow application of the study results to the individual patients in your practice.
Once you determine whether a published report applies to your practice, critical appraisal is the next step. Critical appraisal of the internal and external validity of a scientific report is essential to filter the information that can improve individual patient care as well as contribute to an efficient, high quality health care system. Critical appraisal of an article requires an inquisitive and skeptical mindset combined with a basic understanding of scientific and statistical methods.8 Many would say that scientific and statistical methods are only for researchers. Yet these methods are essential in becoming excellent consumers of research and EBM practitioners. This chapter will provide a basic review of methods for searching, critically appraising, and applying evidence, including an introduction to statistical topics essential to a reliable interpretation of trauma literature.
Best evidence rarely comes from a single study; more often it is the final step of a long scientific journey, in which experts collect, appraise, and summarize the findings of several individual studies using a specific, standard methodology.1 Systematic reviews, such as those published by the Cochrane Collaboration or collections of evidence-based readings (eg, Selective Readings in General Surgery at https://www.facs.org/publications/srgs, which includes selections in Trauma), are excellent ways to distill the daunting amount of information available. When first learning about a topic, systematic reviews are an excellent first step. These reviews are commonly attached to a level of evidence, which gauges the confidence of the summative collection of research on a specific topic.
Yet a systematic review is not always available; thus, how will busy health care providers manage the formidable volume of information that becomes available every day, much of which is contradictory? Appraisal is the answer. There are several systems to appraise and grade the level of evidence provided by the literature. For example, the GRADE (Grades of Recommendation, Assessment, Development and Evaluation)9 system follows a detailed stepwise process to rate evidence (http://www.gradeworkinggroup.org/news, accessed May 30, 2015), which is summarized later in this chapter. The Journal of Trauma and Acute Care Surgery recently adapted the GRADE system to gauge the level of uncertainty of individual articles as shown in Table 63-1. Their system retains study design as a major factor in the classification, but recognizes that each type of clinical question (therapeutic, diagnostic accuracy, etc) demands different types of study designs and tolerates different levels of uncertainty.10,11
| Types of Studies | ||||||
|---|---|---|---|---|---|---|
| Level | Therapeutic/care management | Prognostic and epidemiological | Diagnostic tests or criteria | Economic and value-based evaluations | Systematic reviews and meta-analyses | Guide lines |
| Level I |
|
| Testing of previously developed diagnostic criteria in consecutive patients (all compared to “gold” standard) | Sensible costs and alternatives; values obtained from many sources; multi-way sensitivity analyses | Systematic review (SR) or meta-analysis (MA) of predominantly level I studies and no SR/MA negative criteriae | GRADE system |
| Level II |
|
| Development of diagnostic criteria on consecutive patients (all compared to “gold” standard) | Sensible costs and alternatives; values obtained from limited sources; multiway sensitivity analyses | SR/MA of predominantly level II studies with no SR/MA negative criteriae | |
| Level III |
|
| Nonconsecutive patients (without consistently applied “gold” standard) | Analyses based on limited alternatives and costs; poor estimates | SR/MA with up to 2 negative criteriae | |
| Level IV | Prospective or Retrospectivec study using historical controls or having more than 1 negative criteriona |
| Case-control study with no negative criteriaa | No sensitivity analyses | SR/MA with more than 2 negative criteriae | |
| Level V |
|
| No or poor “gold” standard | |||
The determination of the level of evidence of a study involves four steps.
Step 1: Define study type
Therapeutic and care management studies evaluate a treatment efficacy, effectiveness, and/or potential harm, including comparative effectiveness research and investigations focusing on adherence to standard protocols, recommendations, guidelines, and/or algorithms.
Prognostic and epidemiological studies12 assess the influence of selected predictive variables or risk factors on the outcome of a condition. These predictors are not under the control of the investigator(s). Epidemiological investigations describe the incidence or prevalence of disease or other clinical phenomena, risk factors, diagnosis, prognosis, or prediction of specific clinical outcomes and investigations on the quality of health care.
Diagnostic tests or criteria13 studies describe the validity and applicability of diagnostic tests/procedures or of sets of diagnostic criteria used to define certain conditions (eg, definition of adult respiratory distress syndrome, multiple organ failure (MOF), or post-injury coagulopathy).
Economic and value-based evaluations focus on which type of care management can provide the highest quality or greatest benefit for the least cost. Several types of economic-evaluation studies exist, including cost-benefit, cost-effectiveness, and cost-utility analyses. More recently, Porter proposed value-based health care evaluations, in which value was defined as the health outcomes achieved per dollar spent.14,15
Systematic reviews and meta-analyses evaluate the body of evidence on a topic; meta-analyses specifically include the quantitative pooling of data.
Guidelines are systematically developed statements to assist practitioner and patient decisions about appropriate health care for specific clinical circumstances.16
Step 2: Define the research question, the hypothesis(es), and the research design
The research design is the plan used by the investigators to test a hypothesis related to a research question as unambiguously as possible given practical and ethical constraints. Even descriptive and exploratory studies should have research questions and, most of the time, a testable hypothesis. This step is where you assess whether the research design was appropriate to address the research question and test the hypothesis. Certain designs are better than others. Randomized clinical trials (RCTs) remain the paragon of biomedical research, followed by cohort comparative studies, case-control and case series in this order. In RCTs, by randomly distributing patients to the study groups, potential risk factors are more likely to be evenly dispersed. When blinding of patients and investigators is added to the design, bias is further minimized. These processes diminish the risk of confounding factors influencing the results. As a result, the findings generated by RCTs are likely to be closer to the true effect than the findings generated by other research methods.
Controlled experimentation, however, is not always possible or ethical, thus other research models must be utilized to answer research questions.17 Although the application of study designs other than RCTs may be well justified, we must still recognize and beware of the higher level of uncertainty, and consequent lower level of evidence associated with them. Cohort comparative studies and case-control studies include a comparison group, that is, a group of patients who received a different type of care/procedure/test. Alternatively, the investigator can compare the same group of patients before and after an intervention, or use historical controls. The fundamental difference between cohort and case-control studies resides on where they start; that is, the outcome or the intervention/risk factor. In case-control studies, investigators find a group of patients with a specific outcome (eg, patients with severe torso trauma and coagulopathy) and a comparable group of patients without the outcome (eg, patients with severe torso trauma and no coagulopathy); the investigator then compares the incidence of a risk factor (eg, hemodynamic instability in the field), or whether a particular intervention was instituted (eg, plasma in the field). For example, Wu et al18 used a case-control design to compare the bone mineral density (BMD) of 87 elderly patients with hip fractures to 87 elderly patients without hip fractures and found BMD to be significantly lower among patients with the outcome (ie, hip fracture).
In cohort studies, investigators define a group of patients with the risk factor or intervention (eg, severe torso trauma patients who received plasma in the field), and a comparable group without the risk factor or intervention (eg, severe torso trauma patients who did not receive plasma in the field); then the outcomes are compared. To make things more confusing, a case-control study is sometimes a later offspring of a well-planned cohort study, as in the case-control study by Shaz et al19 on post-injury coagulopathy. Although important medical discoveries were done through case-control studies, such as the association of smoking and lung cancer,20 this design has several limitations that place it lower on the evidence hierarchy. These include, but are not limited to, potential for bias in the selection of the control group and uncontrolled confounding in the assessment of the risk factor or intervention.
Case-series evaluate a single group of patients submitted to a type of care/procedure/test without a comparison group. Case-series have a role in rare conditions or to describe a preliminary experience with a new intervention. However, the lack of a comparator lowers our confidence in the findings and they are less likely to change practice. Of course, if this is an innovative treatment for a currently incurable, lethal disease, we may adopt it even with low confidence for lack of better options. The urgency to adopt the new treatment, however, does not change the fact that our confidence is still low, and that further research is crucial to increase our confidence level.
Propensity score matching (PSM) has gained increased popularity in clinical research as an alternative design when RCTs are not possible.21,22,23,24,25 In brief, the propensity score is the probability of treatment assignment conditional on observed (emphasis on observed) baseline characteristics. Each treated patient is matched to one or more control patients with similar propensity scores but who did not receive the intervention. This works well when the intervention is relatively new and there is variation in adoption, with some professionals using it and others not, regardless of indications. There are controversial results regarding how well PSM studies reflect the results of correspondent RCTs. Lonjon et al23 reported no significant differences in effect estimates between RCTs and PSM observational studies regarding surgical procedures. Conversely, Zhang et al21,22 reported that PSM studies tended to report larger treatment effect than RCTs in the field of sepsis, but the opposite was true for studies in critical care medicine. It is likely that differences in populations and differential control of confounding played a role in these disparities.
RCTs control for unmeasured confounders, while a PSM study is only as good as the measured confounders included in the propensity score model. While appraising a PSM study, make sure to inspect the model used to generate the propensity score: were all important confounders or indications included in the model? Was the model goodness-of-fit (ie, how well the model fit the data) reported and appropriate (as discussed later in this chapter)? More on this design will be presented in subsequent sections.
Step 3: Define effect size
Effect size represents the magnitude and the direction of the difference or association between studied groups.26,27 Large effect sizes tend to strengthen the evidence. Although there is no specific threshold to define a large effect, an effect greater than 5 (or <0.2, when the desired direction is to decrease the outcome) in a condition of low to moderate morbidity or mortality (eg, stable femur fracture in a young person) is considered a large effect.6 In highly morbid or lethal conditions (eg, penetrating chest wounds), an effect size greater than 2 (or <0.5) may be considered large enough.
There are several measures of effect size, and some of the most commonly reported are
Relative risk or risk ratio (RR): The RR compares the outcome probability in two groups (eg, with and without an intervention, or with and without a risk factor). When equal to 1, there is no evidence of effect.
Odds ratio (OR): This index compares the odds of the outcome in two groups. Unless the reader is a gambler, the concept of odds is not intuitive, yet because the highly popular logistic regression (discussed later in this chapter) produces odds ratios, this measure is often reported in the literature. Thus, it is important we understand it. For example, in a group of pediatric severe trauma admissions:
Odds of death in the group receiving tranexamic acid (TXA): number of deaths/number of survivors
Odds of death in the group not receiving TXA: number of deaths/number of survivors
Odds ratio: Odds of death in the TXA group/odds of death in the non-TXA group
Odds ratios are good estimates of the relative risk when the outcome is relatively rare (<10–20%); however, this is not true when the outcome is more common. In studies with high prevalence of the outcome, odds ratios may exaggerate the association or effect and should be interpreted with caution.28 To illustrate the dangers of misinterpretation of odds ratios, consider the study in the area of health disparities by Schulman and colleagues titled “Effects of Race and Sex on Physicians’ Referrals for Cardiac Catheterization” published in the New England Journal of Medicine (NEJM) in 1999.29 In this experiment, doctors were asked to predict compliance and potential benefit from revascularization for cases portrayed by actors of different races and sex. A logistic regression model showed that Black race was associated with a lower likelihood of receiving a referral to cardiac catheterization with an odds ratio of 0.4. The authors concluded that the “race and sex of a patient independently influence how physicians manage chest pain.” Their study received extensive coverage in the news media, including a feature story on ABC’s Nightline, with Surgeon General David Satcher providing commentary.30 For the most part, the media interpreted the findings as “Blacks were 40% less likely to be referred for cardiac testing than Whites.” In a subsequent NEJM Sounding Board article, Schwartz and colleagues called attention for the dangers of using the odds ratios as an effect size measure when the outcome (referral for cardiac catheterization) was very common (>80% in the Schulman et al.’s study). The odds ratio, in this case, led to a gross exaggeration of the actual relative risk: the reported odds ratio of 0.6 ([Blacks referred/Blacks not referred]/[Whites referred/Whites non referred]) actually corresponded to a risk ratio of 0.93. In other words, Blacks were, at most, 7% less likely than Whites to receive the referral for further cardiac testing. Quite a difference! When faced with the report of odds ratios in studies with outcomes more frequent than 20%, one can use the formula proposed by Zhang and Yu28 to obtain an estimate of the relative risk, as follows:
Relative risk (or risk ratio) = odds ratio/[(1 – Po) + (Po × odds ratio)]
where Po is the probability of the event in the control (or reference) group.
Although this formula has been criticized for overestimating the risk ratio (although the overestimation was less pronounced than in logistic regression derived odds ratio),31 it is a simple formula that can assist the reader in obtaining a more realistic estimate of the effect size when the odds ratio was inappropriately used.
Cohen’s d: This measurement is the standardized mean difference; it is not commonly reported, but can be easily calculated as (mean 1 – mean 2)/(pooled standard deviation).26 There are several free online calculators of the Cohen’s d (eg, Ellis PD. Effect size calculators [2009] at http://www.polyu.edu.hk/mm/effectsizefaqs/calculator/calculator.html. Accessed April 15, 2015; and Soper D. Statistics calculators version 3.0 beta. http://danielsoper.com/statcalc3/default.aspx.; Lee A. Becker. Effect size calculators. http://www.uccs.edu/lbecker/index.html, both accessed April 16, 2015). Cohen’s d around 0.2 are considered small, 0.5, medium, and more than or equal to 0.8, large.
Correlation: Pearson’s correlation coefficient r (or its nonparametric equivalent the Spearman’s Rho) measures the correlation between two continuous outcomes (eg, volume transfused and systolic blood pressure) and ranges from –1 to 1. Cohen (the same statistician who proposed the Cohen’s d) suggested the following rule of thumb for correlations: small = |0.10|, medium = |0.30|, and large = |0.50|.32
Step 4: Assess the limitations of the study
The next step recognizes that all research designs, even RCTs, are more or less limited by confounding, bias, inadequate sample size and statistical power, heterogeneity of included subjects, differences between control and study groups, missing data, loss to follow-up, etc. These factors increase the uncertainty surrounding the findings of an investigation and, consequently, decrease its level of evidence. They will be explored in detail in the next sections of the chapter.
In previous sections of the chapter we briefly defined study designs. The classic hierarchy of study design was based on their ability to decrease bias and confounding and ranked the research design in the following order: (1) Systematic reviews and meta-analyses; (2) RCTs with confidence intervals (CIs) that do not overlap the threshold of clinically significant effect; (3) RCTs with point estimates that suggest clinically significant effects but with overlapping CIs; (4) Cohort studies; (5) Case-control studies; (6) Cross sectional surveys; and (7) Case reports.33 Currently, however, several investigators and organizations recognize that most clinical trials fail to provide the evidence needed to inform medical decision making.34 Thus we must use the best research design available to define the best evidence.35
Randomized clinical trials are considered the most unbiased design because random group assignment provides an unbiased treatment allocation and often (but not always) results in similar distribution of confounders across study arms. Ultimately, the goal of randomization is “to ensure that all patients have the same opportunity or equal probability of being allocated to a treatment group.”36 Random allocation means that each patient has an equal chance of being given each experimental group, and the assignment cannot be predicted for any individual patients.37 However, emergency trauma research imposes difficulties to randomization as enrollment is time sensitive and the interventions must be made available without any delay.38,39 In emergency research trials, the patients are not recruited, they are enrolled as they suffer an injury, in a completely random fashion. If effective, randomization creates groups of patients at the start of the study with similar prognoses; therefore, the trial results can be attributed to the interventions being evaluated.40
How to conduct effective randomizations is a challenge in emergency and trauma research. Conventional randomization schemes (eg, sealed envelope with computer-generated random assignment) can impose unethical delays in providing treatment. Another major obstacle of complex randomizations schemes in emergency research is adherence to protocol, thus alternative schemes (eg, prerandomization in alternate weeks) have been proposed.41 In a recent trial, we randomized severely injured patients for whom a massive transfusion protocol was activated to two groups: (1) viscoelastic (thrombelastography)-guided, goal-directed massive transfusion or (2) conventional coagulation assays (eg, prothrombin time, etc) and balanced blood product ratios on predefined alternating weeks.42 The system was formidably successful in producing comparable groups at baseline. Another example is the Prehospital Acute Neurological Treatment and Optimization of Medical care in Stroke Study (PHANTOM-S), published in 2014, in which patients were randomly assigned weeks with and without availability of a Stroke Emergency Mobile.43 These alternative randomization approaches are recognized as appropriate in emergency research.38
Adaptive designs, including adaptive randomization, have been proposed to make trials more efficient.44,45 A 2015 draft guidance document from the Food and Drug Administration defines an adaptive design clinical study as “a study that includes a prospectively planned opportunity for modification of one or more specified aspects of the study design and hypotheses based on analysis of data (usually interim data) from subjects in the study.”46 For example, the recently published PROPPR trial used an adaptive design to grant their Data and Safety Monitoring Board authority to increase the sample size and reach adequate power.47 Their initial sample size (n = 580) was planned to detect a clinically meaningful 10% points difference in 24-hour mortality based on previous evidence. The DSMB recommended increasing the sample size to 680 based on the results on an interim analysis.
In sum, the research design must be appropriate to the research question, ethical and valid, both internally and externally. Internal validity refers to the extent to which the results of the study are biased or confounded. In the next sections, we will discuss bias and confounding in more detail, but basically this comes down to one question: Is the association between outcome and effect reported in the study real? How much of it may be due to bias and/or confounders? External validity, on the other hand, reflects to which extent the study is generalizable.
When researchers used data collected for the purpose of addressing the research question, they are using primary data. On the other hand, in the era of “Big Data,” it is common to see the use of secondary data, collected for purposes unrelated to the specific research question. There are undeniable advantages on secondary datasets, as they are usually large and inexpensive. Yet they have had mixed results when used for tasks as risk adjustment.48,49 Administrative datasets collected for billing purposes, for example, are often influenced by financial reasons, which can favor overcoding or undercoding, may and have the number of diagnoses capped or deincentivized due to declining marginal returns in billings.49,50
In addition, medical coding and clinical practices are subject to changes over time due to a variety of reasons. For example, the coding of “illegal drugs” upon trauma admission is likely to change in unpredictable ways in states where cannabis became a legal, recreational drug. Another glaring example relates to collection and coding of the social construct variable “race and ethnicity,” which has changed dramatically over the past few decades.51 Comorbidities may be misdiagnosed as complications and vice versa. To address this problem, since 2008, most hospitals now report a “present on admission” (POA) for each diagnosis in its administrative data as a means to distinguish hospital-acquired conditions from comorbidities.50 Of course using data from before and after modifications, such as the inclusion of a POA code, were implemented affect the internal validity of the study. Whenever longitudinal data are used in a study, especially if covering long periods of time, it is important to verify whether there were changes in data collection, health policies, regulations, etc that can potentially affect the data.
Sometimes the distinction between primary and secondary data becomes blurry, as it happens in registries such as state-mandated and hospital-based trauma registries or the National Trauma Data Bank, a voluntary, national trauma dataset maintained by the American College of Surgeons. These datasets were developed to provide a comprehensive epidemiological characterization of trauma, thus one can assume that when the research question is related to frequency, risk factors, treatments, and prognosis of trauma, these represent legitimate primary data. However, registries may lack the granularity to address study hypotheses; for example, analyzing the effects of early transfusions of blood components on coagulation-related deaths. In the end, In addition, low volume hospitals may not contribute enough to aggregate estimates biasing mortality toward high volume facilities. The Center for Surgical Trials and Outcomes Research (Department of Surgery, The Johns Hopkins School of Medicine), Baltimore, has done a commendable effort documenting differences in risk adjustment and, more important, providing standardize analytic tools to improve risk adjustment and decrease low-volume bias in studies using the NTDB.52,53,54
All studies that use a statistical test, even purely descriptive studies, have hypotheses. That is because a statistical test is based on a hypothesis. Every hypothesis can be placed in the following format:
Variable X distribution in Group A
is different (or not different) from
Variable X distribution in Group B
Despite its simplicity, this is a widely applicable model for constructing hypotheses.55 It sets the stage for elements that must be included in the methods section. The authors must define what characterizes Group A and Group B and what makes them comparable (aside from Variable X). Variable X, which is the variable of interest, must be defined in a way that allows the reader to completely understand how the variable is measured. The hypotheses should be defined using the above mentioned PICO framework. For example, “we hypothesize that adult trauma patients (P) receiving pharmacoprophylaxis for venous thromboembolism (I) will have fewer venous thromboembolisms (O) than patients not receiving pharmacoprophylaxis (C).’’
The commonly reported p-value is the probability of obtaining the observed effect (or larger) under the null hypothesis that there is no effect.56 Colloquially, we can interpret the p-value as the probability that the finding was the result of chance.57 The p-value is the chance of committing what is called a type 1 error, that is, wrongfully rejecting the null hypothesis (ie, accepting a difference when in reality there is none). Now, more important, what the p-value is not: “how sure one can be that the difference found is the correct difference.”
Significance is the level of the p-value below which we consider a result “statistically significant.” It has become a worldwide convention to use the 0.05 level, although it is completely arbitrary, not based on any objective data, and, in fact, inadequate in several instances. It was suggested initially by the famous statistician Ronald Fisher, who rejected it later and proposed that researchers reported the exact level of significance.58
The readers will often see in research articles that p-values were “adjusted for multiple comparisons,” resulting in significance set at p-values smaller than the traditional 0.05 threshold. This is one of the most controversial issues in biostatistics, with experts debating the need for such adjustment.59,60,61 Those who defend the use of multiple comparisons adjustments claim that multiple comparisons increase the chances of finding a p-value less than 0.05 and inflate the likelihood of a type 1 error.60 Those who criticize its use argue that this leads to type 2 errors, that is, the chance of not finding a difference when indeed there is one.59,60,61 One of the authors of this chapter (Angela Sauaia) recalls her biostatistics professor claiming that, if multiple comparisons indeed increased type 1 error, then biostatisticians should stop working at the age of 40, as any differences after then would be significant just by chance. Our recommendation is: if the hypotheses being tested were predefined (ie, before seeing the data), then multiple comparisons adjustment is probably unnecessary; however, if hypothesis testing was motivated by trends in the data, then it is possible that even the most restrictive multiple comparison adjustment will not be able to account for the immense potential for investigator bias. In the end, the readers should check the exact p-values and make their own judgment about a significance threshold based on the impact of the condition under study. Lethal conditions for which there are few or no treatment options may require looser significance cutoffs, while, at the other end of the spectrum, benign diseases with many treatment options may demand strict significance values.
A special case of multiple comparisons is the interim analyses, which are preplanned, sequential analyses conducted during a clinical trial. These analyses are almost obligatory in contemporary trials due to cost and ethical factors. The major rationale for interim analyses relies on the ethics of holding subjects hostage of a fixed sample size, when a new therapy is potentially harmful, overwhelmingly beneficial or futile. Interim analyses allow investigators, upon a Data Safety Monitoring Board (DSMB) independent committee advice, to stop a trial early due to efficacy (the tested treatment has already proven to be of benefit), or futility (the treatment-control difference is smaller than a predetermined value), or harm (treatment resulted in some harmful effect).62 For example, Burger et al in their RCT testing the effect of prehospital hypertonic resuscitation after traumatic hypovolemic shock reported that the DSMB stopped the study on the basis of potential harm in a preplanned subgroup analysis of non-transfused subjects.63
The 95% CI, a concept related to significance, means that, if we were to repeat the experiment multiple times, and, at each time, calculate a 95% CI, 95% of these intervals would contain the true effect. A more informal interpretation is that the 95% CI represents the range within which we can be 95% certain that the true effect lies. Although the calculation of 95% CI is highly related to the process to obtain the p-value, the CIs provide more information on the degree of uncertainty surrounding the study findings. There have been initiatives to replace the p-value by 95% CI, met with much resistance. Most journals now require that both are reported.
For example, in the CRASH-2 trial, a randomized controlled study on the effects of TXA in bleeding trauma patients, the TXA group showed a lower death rate (14.5%) than the placebo group (16.0%) with p-value = 0.0035.64 We can interpret this p-value as: “There is 0.35% chance that the difference in mortality rates was found by chance.” The authors also reported the effect size as a relative risk of 0.91 with a 95% CI of 0.85–0.97. This means, in a simplified interpretation, that we can be 95% certain that the true relative risk lies between 0.85 and 0.97. Some people prefer to interpret the effect as an increase; in which case one just needs to calculate the inverse: 1/0.91 = 1.10; 95% CI: 1.03–1.18. If the authors did not provide the 95% CI, you can visit a free, online statistics calculator (eg, www.vassarstats.net), to easily obtain the 95% CI of the difference of 1.5% points: 0.5–2.5% points. In an abridged interpretation, we can be 95% certain that the “true” difference lies between 0.5% and 2.5% points. Incidentally, notice that we consistently use “percent points” to indicate that this is an absolute (as opposed to relative) difference between two percentages.
The example above reminds us that it is important to keep in mind that statistical significance does not necessarily mean practical or clinical significance. Small effect sizes can be statistically significant if the sample size is very large. The above mentioned CRASH-2 trial, for example, enrolled 20,211 patients.64 P-values are related to many factors extraneous to whether the finding was by chance or not: including the effect size (larger effect sizes usually produce smaller p-values), sample size (larger samples sizes often result in significant p-values) and multiple comparisons (especially when unplanned and driven by the data).65
In addition, we must make sure that the study used appropriate methods for hypothesis testing. Statistical tests are based on assumptions, and if these assumptions are violated, the tests may not produce reliable p-values. Many tests (eg, t-test, ANOVA, Pearson correlation) rely on the normality assumption. The Central Limit Theorem (the distribution of the average of a large number of independent, identically distributed variables will be approximately normal, regardless of the underlying distribution) and the law of large numbers (the sample mean converges to the distribution mean as the sample size increases) are often invoked to justify the use of parametric tests to compare non-normally distributed variables. However, these allowances apply to large (n > 30) samples; gross skewness and small sample sizes (n < 30) will render parametric tests inappropriate. Thus, if the data are much skewed, as it is often the case with number of blood product units transfused, length of hospital stay, and viscoelastic measurements of fibrinolysis (eg, clot lysis in 30 minutes), or the sample size is small (as it is often the case in basic science experiments), nonparametric tests (eg, Wilcoxon rank-sum, Kruskal-Wallis, Spearman correlation, etc) or appropriate transformations (eg, log, Box-Cox power transformation) to approximate normality are more appropriate. More on this topic in the section on sample descriptors.
Statistical power is the counterpart to the p-value. It relates to type 2 error, or the failure to reject a false null hypothesis (a “false negative”). Statistical power is the probability of accepting the null hypothesis when there is actually a difference. Despite its importance, it is one of the most neglected aspects of research articles. Most studies are superiority studies, that is, the researchers are searching for a significant difference. When a difference is not found in a superiority study, there are two alternatives: to declare “failure to find a significant difference” or to report a power analysis to determine how confident we can be to declare the interventions (or risk factors) under study indeed equivalent. The latter alternative is more appealing when it is preplanned as an equivalence or non-inferiority trial rather than an afterthought in a superiority study.
Whether statistical power is calculated beforehand (ideally) or afterwards (better than not at all), it must always contain the following four essential components: (1) power: usually 80% (another arbitrary cutoff), (2) confidence: usually 95%, (3) variable value in the control group/comparator, and (4) difference to be detected. For example, Burger et al stated in the above mentioned prehospital hypertonic resuscitation RCT63:
The study was powered to detect a 4.8% overall difference in survival (from 64.6% to 69.4%) between the NS group and at least 1 of the 2 hypertonic groups. These estimates were based on data from a Phase II trial of similar design completed in 2005.8 There was an overall power of 80% (62.6% power for individual agent) and 5 planned interim analyses. On the basis of these calculations a total sample size of 3726 patients was required.
We call attention to how the difference to be detected was based on previous evidence. The difference to be detected is mostly a clinical decision based on evidence. Power should not be calculated based on the observed difference: we determine the appropriate difference and then obtain the power to detect such difference. The basic formula to calculate power is shown below:
where N is the sample size in each group (assuming equal sizes), σ is the standard deviation of the outcome variable, Zb represents the desired power (0.84 for power = 80%), Za/2 represents the desired level of statistical significance (1.96 for alpha = 5%), and “difference” is the proposed, clinically meaningful difference between means. There are free, online power calculators; however, they usually are meant for simple calculations. Power analysis can become more complex when we need to take into account multiple confounders (covariates), in which case the correlation between the covariates needs to be taken into account, or when cluster effects (explained in more detail later) exist, when an inflation factor, dependent on the level of intracluster correlation and number of clusters, is used to estimate the sample size.
Equivalence and noninferiority studies are becoming much more common in the era of comparative effectiveness.66,67 Their null hypothesis assumes that there is a difference between arms, while for the more common superiority trials the null hypothesis assumes that there is no difference between groups. A noninferiority trial seeks to determine whether a new treatment is not worse than a standard treatment by more than a predefined margin of noninferiority for one or more outcomes (or side effects or complications). Noninferiority trials and equivalence trials are similar, but equivalence trials are two-sided studies, where the study is powered to detect whether the new treatment is not worse and not better than the existing one. Equivalence trials are not common in clinical medicine.
In noninferiority studies, the researchers must prespecify the difference they intend to detect, known as the noninferiority margin, or irrelevant difference or clinical acceptable amount.66 Within this specified noninferiority margin, the researcher is willing to accept the new treatment as noninferior to the standard treatment. This margin is determined by clinical judgment combined with statistical factors and is used in the sample size and power calculations. For example, is a difference of 4% in infection rates between two groups large enough to sway your decision about antibiotics? Would a difference of 10% make you think they are different? Or you need something smaller? These decisions are based on clinical factors such as severity of the disease, and variation of the outcomes.
The USA Multicenter Prehospital Hemoglobin-based Oxygen Carrier Resuscitation Trial is an example of a dual superiority/noninferiority assessment trial.68 The noninferiority hypothesis assumed that patients in the experimental group would have no more than a 7% higher mortality rate compared with control patients, based on available medical literature. The noninferiority question in this study was that the blood substitute product would be used in scenarios in which blood products were needed but not available or permissible. Incidentally, this is another example of where adaptive power analysis was performed after enrollment of 250 patients to ensure that no increase in the trial size was necessary.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree