Chapter 4
A Mathematical Model of Gonadotropin-Releasing Hormone Neurons
James Sneyd, Wen Duan and Allan Herbison
Department of Mathematics, University of Auckland, New Zealand
Department of Physiology, University of Otago, New Zealand
4.1 Introduction
Gonadotropin-releasing hormone (GnRH) neurons exhibit complex patterns of electrical spiking. Action potentials occur in groups, often called bursts, and each burst is closely correlated with an increase in the concentration of intracellular 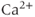 . Each burst is separated by a quiet interval with no action potentials, of length ranging from a few seconds to a few tens of seconds. Although it is unclear exactly what is the physiological function of these patterns of electrical bursting, it is highly likely that they play a role in the regulation of the release of GnRH from the nerve terminal in the median eminence of the hypothalamus. GnRH in turn controls the release from the anterior pituitary of luteinizing hormone and follicle-stimulating hormone, which are crucial for sexual development and fertility. Thus, there is ample motivation for the study of the mechanisms underlying the patterns of electrical spiking seen in GnRH neurons.
. Each burst is separated by a quiet interval with no action potentials, of length ranging from a few seconds to a few tens of seconds. Although it is unclear exactly what is the physiological function of these patterns of electrical bursting, it is highly likely that they play a role in the regulation of the release of GnRH from the nerve terminal in the median eminence of the hypothalamus. GnRH in turn controls the release from the anterior pituitary of luteinizing hormone and follicle-stimulating hormone, which are crucial for sexual development and fertility. Thus, there is ample motivation for the study of the mechanisms underlying the patterns of electrical spiking seen in GnRH neurons.
Because of the highly complex dynamical phenomena observed in GnRH neurons (and, indeed, many other types of neurons), mathematical models have an important role to play. It is difficult, if not impossible, to attain a detailed understanding of the mechanisms underlying electrical bursting, and other kinds of complex oscillations, using qualitative models alone. Qualitative models (i.e., nonmathematical explanations of the behavior) are important for suggesting underlying structures and possible mechanisms, but, to test whether or not such mechanisms actually work, and to make specific predictions, a mathematical model is necessary.
Neuroendocrine neurons have, in general, some features of particular interest to modelers. The complex electrical bursting behavior is necessarily a combination of at least two different oscillatory processes –one oscillatory process giving the fast electrical spiking, and the other, slower, process, causing the transitions from bursting to nonbursting regions. Although this must be true in general, it has not proven to be an easy task to determine exactly what each of these mechanisms is.
The fast spiking is reasonably well understood in many cell types, being the result of the modulation by the voltage of ionic conductances (usually, 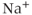 and
and 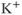 conductances) in the plasma membrane. Models of such fast spiking are usually based, more or less explicitly, on the model of Hodgkin and Huxley (1952). The precise nature of the conductances change, as do the parameter values, but the underlying model structure remains essentially the same.
conductances) in the plasma membrane. Models of such fast spiking are usually based, more or less explicitly, on the model of Hodgkin and Huxley (1952). The precise nature of the conductances change, as do the parameter values, but the underlying model structure remains essentially the same.
However, the nature of the slow process (or processes) that causes the transitions between silent and active phases remains elusive, and is almost certainly different in each cell type. Some models use the intrinsic oscillatory dynamics of intracellular 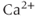 as the additional slow process (Chay and Keizer, 1983). Others use mechanisms based on metabolism or mitochondrial transport (Bertram et al., 2004, 2007a,b).
as the additional slow process (Chay and Keizer, 1983). Others use mechanisms based on metabolism or mitochondrial transport (Bertram et al., 2004, 2007a,b).
Ultimately, it is not an easy task to determine the exact combination of oscillatory processes that causes bursting oscillations in any particular cell type. Mostly, models strive to present possible hypotheses which can then be tested, leading to the refinement of the models and additional tests. As this cycle of experiment and theory progresses through multiple models, we hope to get closer to an understanding of what is actually happening in the cell.
Here, we present a model of electrical bursting in GnRH neurons, a model that has already assisted us in understanding some of the basic mechanisms that control the length of the burst, and the length of the interburst interval.
4.1.1 Experimental data
The experimental results on which our model is based are described in detail by Lee et al. (2010). Here, we present only a very brief description. Intracellular calcium concentration and membrane potential were measured simultaneously in GnRH neurons in brain slices from GnRH-Pericam transgenic mice. Three different subpopulations of GnRH neurons were found. In one subpopulation (about 41%), there were no spontaneous action potentials, although action potentials could be stimulated by depolarization with KCl. In the second, small, subpopulation (3%), the action potentials were continuous, but not associated with a transient rise in 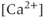 , while in the third subpopulation (56%), bursts of electrical spikes were accompanied by
, while in the third subpopulation (56%), bursts of electrical spikes were accompanied by 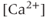 transients. It is this third subpopulation only that we consider here.
transients. It is this third subpopulation only that we consider here.
For a bursting GnRH neuron, there is a clear correlation between the bursts of action potentials (or, more precisely, action current (AC) spikes) and the corresponding 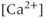 transients (Figure 4.1a). The interburst interval varies from about 10 s to about 60 s, and the number of AC spikes within a burst is mostly between 2 and 10. The
transients (Figure 4.1a). The interburst interval varies from about 10 s to about 60 s, and the number of AC spikes within a burst is mostly between 2 and 10. The 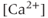 transients are synchronized with the short bursts (Figure 4.1a). Importantly, the peak of the
transients are synchronized with the short bursts (Figure 4.1a). Importantly, the peak of the 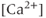 transient occurs a few seconds after the burst has ended.
transient occurs a few seconds after the burst has ended.
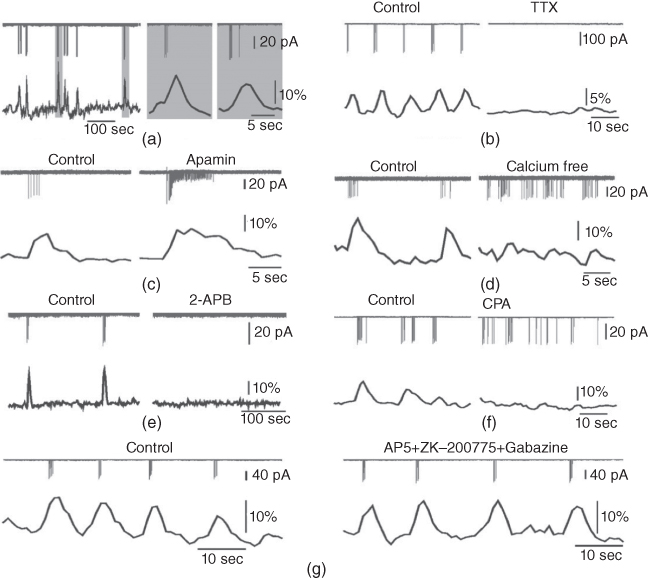
Figure 4.1 Recorded behavior of live GnRH neurons in the acutely prepared mouse brain slice, adapted from Lee et al. (2010). In each panel, the upper traces are the action currents, and the lower traces are the intracellular  transients. (a) Spontaneous short bursts are associated with long duration (about 10 s)
transients. (a) Spontaneous short bursts are associated with long duration (about 10 s)  transients. (b) A blocker of voltage-gated
transients. (b) A blocker of voltage-gated 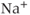 channel, tetrodotoxin (TTX, 0.5
channel, tetrodotoxin (TTX, 0.5 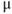 M). (c) A blocker of
M). (c) A blocker of 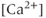 -dependent
-dependent 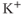 channels, apamin (300 nM). (d) Extracellular zero
channels, apamin (300 nM). (d) Extracellular zero 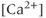 solution. (e) A blocker of inositol trisphosphate receptors, 2-aminoethoxydiphenyl borate (2-APB, 100
solution. (e) A blocker of inositol trisphosphate receptors, 2-aminoethoxydiphenyl borate (2-APB, 100 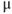 M). (f) An inhibitor of sarco/endoplasmic reticulum
M). (f) An inhibitor of sarco/endoplasmic reticulum 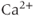 ATPase, cyclopiazonic acid (CPA, 30
ATPase, cyclopiazonic acid (CPA, 30 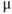 M). (g) Ionotropic glutamate and
M). (g) Ionotropic glutamate and 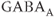 receptor blockers (AP-5 20
receptor blockers (AP-5 20 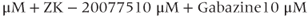 ).
).
Although there is a clear evidence of stochasticity, both in the intraburst spiking pattern and in the interburst interval, here we shall focus our attention on deterministic mechanisms for controlling the bursting pattern. This allows for a simpler analysis of the model, while preserving the majority of the important dynamic features of the bursting, such as the interspike interval.
To investigate the mechanisms underlying this bursting behavior, pharmacological manipulations were used to perturb potential  , influx mechanisms, and other ionic currents. Tetrodotoxin (TTX; a
, influx mechanisms, and other ionic currents. Tetrodotoxin (TTX; a 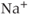 channel blocker) depresses both AC spikes and
channel blocker) depresses both AC spikes and 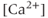 transients (Figure 4.1b). This suggests that the activation of the voltage-dependent
transients (Figure 4.1b). This suggests that the activation of the voltage-dependent 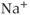 channel is needed for the initiation of an AC spike, with
channel is needed for the initiation of an AC spike, with 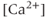 transients following. Apamin, a blocker of
transients following. Apamin, a blocker of 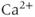 -activated
-activated 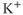 channels (SK channels), highly increases the number of spikes within each burst, but has little effect on the
channels (SK channels), highly increases the number of spikes within each burst, but has little effect on the 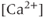 transients (Figure 4.1c). In the absence of extracellular
transients (Figure 4.1c). In the absence of extracellular 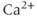 ,
, 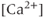 transients are almost eliminated while the bursting pattern is disorganized (Figure 4.1d).
transients are almost eliminated while the bursting pattern is disorganized (Figure 4.1d).
Interestingly, blockers of the inositol trisphosphate (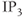 ) receptor (IPR), such as 2-APB or Xestospongin, also eliminate both AC bursting and
) receptor (IPR), such as 2-APB or Xestospongin, also eliminate both AC bursting and 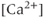 transients (Figure 4.1e). The IPR is a
transients (Figure 4.1e). The IPR is a 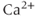 channel located on the membrane of the endoplasmic reticulum (ER) that is activated by the second messenger
channel located on the membrane of the endoplasmic reticulum (ER) that is activated by the second messenger 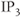 .
. 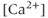 has a biphasic effect on the IPR; at low
has a biphasic effect on the IPR; at low 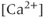 , the steady-state open probability of the IPR increases with
, the steady-state open probability of the IPR increases with 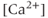 , but at high
, but at high 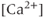 , the reverse is true. Thus, the IPR mediates a phenomenon known as
, the reverse is true. Thus, the IPR mediates a phenomenon known as 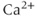 -induced
-induced 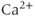 release. When
release. When 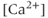 is low, a small increase in
is low, a small increase in 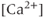 increases the open probability of the IPR, which then releases additional
increases the open probability of the IPR, which then releases additional 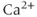 from the ER, leading to a large
from the ER, leading to a large 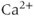 transient. When
transient. When 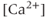 is high enough, the IPR shuts off, and the
is high enough, the IPR shuts off, and the 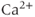 transient returns to baseline.
transient returns to baseline.
When the intracellular 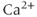 store is emptied by inhibiting the sarco/endoplasmic reticulum
store is emptied by inhibiting the sarco/endoplasmic reticulum 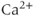 ATPase pumps (SERCA pumps) with cyclopiazonic acid (CPA),
ATPase pumps (SERCA pumps) with cyclopiazonic acid (CPA), 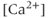 transients are strongly depressed, while the pattern of short bursts is again disorganized (Figure 4.1f).
transients are strongly depressed, while the pattern of short bursts is again disorganized (Figure 4.1f).
Since 2-APB blocks the IPR, it prevents 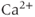 -induced
-induced 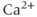 release and so eliminates the
release and so eliminates the 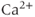 transients. At first glance, the fact that 2-APB also eliminates electrical spiking would seem to indicate that it is the
transients. At first glance, the fact that 2-APB also eliminates electrical spiking would seem to indicate that it is the 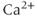 transient which initiates the action potential spiking, not vice versa, as suggested by the response to TTX. This is a discrepancy we shall be considering in more detail later.
transient which initiates the action potential spiking, not vice versa, as suggested by the response to TTX. This is a discrepancy we shall be considering in more detail later.
The AC spikes and 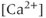 transients continue even after blocking ionotropic glutamate and
transients continue even after blocking ionotropic glutamate and 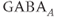 receptors with a combination of receptor blockers (AP5,ZK-200775 and gabazine for NMDA, AMPA, and
receptors with a combination of receptor blockers (AP5,ZK-200775 and gabazine for NMDA, AMPA, and 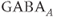 receptors, respectively, Figure 4.1g), from which we conclude that GnRH neurons have an intrinsic capacity to generate bursting, that is, the bursts are not generated by synaptic input from elsewhere. Although we know that neither GABA nor glutamate input is necessary to drive bursting in GnRH neurons (Lee et al., 2012) – and, indeed, the blockage of GABA/glutamate signaling has little effect on the burst properties – one has to be careful with this assumption, as it is possible that other afferent inputs play a regulatory role. However, our data indicate that, although afferent input may have a role to play, each GnRH neuron has an intrinsic capacity to generate electrical bursting, and it is this intrinsic capacity that is the major focus of our modeling efforts.
receptors, respectively, Figure 4.1g), from which we conclude that GnRH neurons have an intrinsic capacity to generate bursting, that is, the bursts are not generated by synaptic input from elsewhere. Although we know that neither GABA nor glutamate input is necessary to drive bursting in GnRH neurons (Lee et al., 2012) – and, indeed, the blockage of GABA/glutamate signaling has little effect on the burst properties – one has to be careful with this assumption, as it is possible that other afferent inputs play a regulatory role. However, our data indicate that, although afferent input may have a role to play, each GnRH neuron has an intrinsic capacity to generate electrical bursting, and it is this intrinsic capacity that is the major focus of our modeling efforts.
4.2 Previous models of GnRH neurons
Much of the previous modeling work on GnRH neurons has been based not on data from GnRH neurons themselves, but on data from analogous cell lines, such as GT1 cells. Although these early models, thus, have only limited direct applicability to GnRH neurons in slice preparations, they still remain the basis for all subsequent modeling work.
The earliest models of electrical spiking in GT1 cells were those of Van Goor et al. (2000) and LeBeau et al. (2000). These models have the same basic structure as the Hodgkin–Huxley equations. Thus,
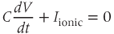
where 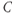 is the membrane capacitance and
is the membrane capacitance and 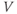 is the potential difference across the cell membrane. (For an introductory discussion of the Hodgkin–Huxley model and a brief look at the mathematical theory of that model, see Keener and Sneyd (2008).)
is the potential difference across the cell membrane. (For an introductory discussion of the Hodgkin–Huxley model and a brief look at the mathematical theory of that model, see Keener and Sneyd (2008).)
In the LeBeau model, there were nine different ionic conductances:
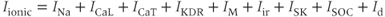
where 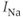 is a TTX-sensitive
is a TTX-sensitive 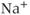 current,
current, 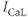 and
and  are L-type and T-type
are L-type and T-type 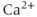 currents, and
currents, and 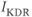 ,
, 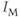 , and
, and 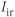 are delayed-rectifier, M-type, and inward-rectifier
are delayed-rectifier, M-type, and inward-rectifier 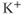 currents.
currents. 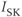 is a
is a 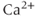 -activated
-activated 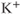 current, while
current, while 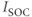 is a store-operated
is a store-operated 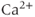 channel, that is, a
channel, that is, a 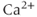 channel that opens when the endoplasmic reticulum is depleted of
channel that opens when the endoplasmic reticulum is depleted of 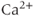 . Finally,
. Finally, 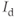 is a nonselective inward cation current.
is a nonselective inward cation current.
Each of these currents is modeled as the product of a conductance, some gating variables, and a linear current–voltage curve. Thus, for example,
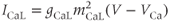
where 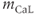 is a time-dependent gating variable satisfying the equation
is a time-dependent gating variable satisfying the equation
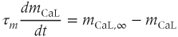
 is the channel conductance, and
is the channel conductance, and 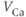 is the Nernst potential of
is the Nernst potential of 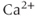 . Many of the gating variables were set at their steady states, for simplicity.
. Many of the gating variables were set at their steady states, for simplicity.
In the model of Van Goor et al. (2000), there was no detailed model of the intracellular 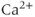 dynamics, but this was substantially improved in the subsequent version of LeBeau et al. (2000). In the LeBeau model, spiking was essentially caused by the
dynamics, but this was substantially improved in the subsequent version of LeBeau et al. (2000). In the LeBeau model, spiking was essentially caused by the 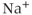 and
and 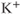 currents, with the frequency modulated by the three pacemaker currents,
currents, with the frequency modulated by the three pacemaker currents, 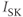 ,
, 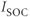 , and
, and 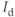 , all three currents being coupled to the intracellular
, all three currents being coupled to the intracellular 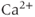 concentration, and thus to the
concentration, and thus to the 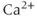 influx through
influx through  and
and 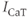 .
.
One of the most interesting results of the LeBeau model was their prediction of the existence of a nonselective cation current, 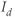 , activated by cAMP and inhibited by
, activated by cAMP and inhibited by 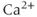 . Although they were unable to confirm the existence of this current experimentally, the model still demonstrated the components needed to explain the experimental results.
. Although they were unable to confirm the existence of this current experimentally, the model still demonstrated the components needed to explain the experimental results.
The 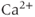 handling in this model was further improved by Fletcher and Li (2009), who constructed a spatial model of the intracellular
handling in this model was further improved by Fletcher and Li (2009), who constructed a spatial model of the intracellular 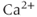 , as well as simplifying the currents in the model.
, as well as simplifying the currents in the model.
In a series of papers, Roberts and Suter and others (Roberts et al., 2006, 2008b; Roberts and Suter, 2008; Roberts et al., 2008a; 2009; Hemond et al., 2012) constructed a GnRH model of a rather different type. Although their model was also based to an extent on the earlier work of LeBeau and van Goor, Roberts and Suter constructed a more complex compartmental model using the software package GENESIS (http://www.genesis-sim.org), and determined some of the parameters (the membrane resistance, the membrane capacitance and the axial resistance) by fitting to experimental data. The other parameters were taken from previous work, mostly from the LeBeau and van Goor models. GENESIS is a tool for constructing compartmental models of spatially distributed neurons, and was used to construct a model that gave excellent agreement with the shape of the individual action potentials in each burst. They also performed an elementary bifurcation analysis on a single-compartment version of the model, although their analysis did not focus on the mechanisms of bursting.
Possibly the most comprehensive model to date of GnRH neurons in vivo is that of Csercsik et al. (2012). They incorporated the earlier models of van Goor and LeBeau with the later model of Lee et al. (2010) to provide a single integrated model that reproduced the shape of the action potentials in detail, as well as incorporating the mechanisms that controlled burst length and interburst interval. Finally, the Csercsik model incorporated a simple form of soma–dendrite interaction, thus including, in a simplified form, the approach of Roberts and Suter.
Overall, these models fall into two main groups. The earlier models of Van Goor et al. (2000) and LeBeau et al. (2000), as well as the model of Fletcher and Li (2009), are based on data from GT1 cells, while the later models of Roberts and Suter (Roberts et al., 2006, 2008b; Roberts and Suter, 2008), Csercsik et al. (2012), and Lee et al. (2010) are based on data from hypothalamic slices, and are, thus, presumably, more applicable to GnRH neurons in vivo. Nevertheless, the later models still rely to a large extent on the earlier modeling work based on GT1 cells, as there are few detailed measurements of electrophysiological parameters of the ion channels in GnRH neurons in brain slices.
4.3 A model of GnRH neurons in hypothalamic slices
Given the plethora of existing models of GnRH neurons, it is natural to ask why another model is needed. To answer this question, it is important first to make clear exactly which data the model is designed to explain, and what is the purpose of the model. Essentially, we are less concerned with the detailed structure of each individual action potential, but are more interested in the mechanisms that determine the bursting structures such as the interburst interval, or the number of action potentials in each burst.
Our original model (Lee et al., 2010) was also designed to answer these same questions, and was successful (at least partially) in doing so. However, the complexity of our original model is such as to make it difficult to extract and understand the important mechanisms that control the bursting. This motivates the construction of a simpler model which nevertheless incorporates the important control mechanisms. Here, we discuss this simpler version of the model.
Because of this particular focus, our simplified model is not a good quantitative description of a single action potential. In this respect, it can compete neither with the work of Roberts and Suter, nor with the integrated model of Csercsik et al. However, the full model has already led to an increased understanding of behaviors on the longer time scale of the bursts, and has led to the discovery of long-lasting 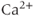 -sensitive hyperpolarising currents which appear to set the interburst interval. Because of this success, it is a worthwhile exercise to simplify the model, so that its underlying structure and behavior can be better understood.
-sensitive hyperpolarising currents which appear to set the interburst interval. Because of this success, it is a worthwhile exercise to simplify the model, so that its underlying structure and behavior can be better understood.
From the typical experimental results shown in Figure 4.1, we conclude:
- Bursting is a spontaneous feature of GnRH neurons, and does not need to be initiated by synaptic input from outside the cell.
- The apamin-sensitive,
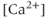 -dependent SK channel is responsible for termination of the electrical bursting.
-dependent SK channel is responsible for termination of the electrical bursting.
- The
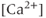 transients consist principally of
transients consist principally of 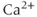 released from internal stores via the IP
released from internal stores via the IP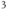 receptor.
receptor.
However, a number of questions remain. Most importantly,
- Which comes first, the
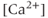 transient or the electrical bursting? On the one hand, the TTX result indicates that the AC bursting initiates the
transient or the electrical bursting? On the one hand, the TTX result indicates that the AC bursting initiates the 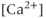 transient, as blocking the bursting also stops the
transient, as blocking the bursting also stops the 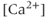 transients. On the other hand, the 2-APB (and Xestospongin) result indicates the reverse, that the
transients. On the other hand, the 2-APB (and Xestospongin) result indicates the reverse, that the 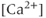 transient initiates the bursting, as the blockage of the
transient initiates the bursting, as the blockage of the 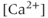 transients also prevents bursting.
transients also prevents bursting.
- Why does a zero external
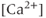 solution increase burst frequency?
solution increase burst frequency?
- The response to apamin shows that the SK channel plays an important role in the termination of bursting. However, what stops the activity between bursts, when
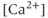 is sitting at its baseline? In the presence of 2-APB, why does the bursting stop at all?
is sitting at its baseline? In the presence of 2-APB, why does the bursting stop at all? - Why does a zero external
Our mathematical model is designed to answer these questions, at least partially. However, as we shall see, the model not only provides plausible answers to these questions, it also predicts that a previously unsuspected  -gated
-gated channel plays a major role in the control of the interburst interval. Experimental investigation subsequently confirmed the existence of this channel in GnRH neurons, and thus the model has also played a useful predictive role.
channel plays a major role in the control of the interburst interval. Experimental investigation subsequently confirmed the existence of this channel in GnRH neurons, and thus the model has also played a useful predictive role.
It is worthwhile considering briefly just how these questions determine, at least partially, the structure of the model that we use to answer them. Firstly, our questions are qualitative, rather than quantitative, and thus we do not aim to build a model that reproduces the exact shape of individual action potentials. We will need to get the statistics of the bursts (histograms of interburst interval, burst length, number of spikes in a burst, etc.) as accurately as possible, but individual spikes are less important for our goals. Secondly, the questions do not address the question of spike propagation, and are thus (possibly) relatively unaffected by spatial considerations. For this initial model, we thus omit any spatial dependencies. (Interestingly, later work by Chen et al. (2013) shows that spatial considerations can be important, but that is not our current goal.) Finally, from the extensive earlier modeling work on GT1 cells and GnRH neurons we have a rough a priori idea of which ionic currents are likely to play a role, and, thus, our model has only limited freedom in which components it may use.
The model equations and parameters are based, to a greater or lesser extent, on the earlier models of Van Goor et al. (2000) and LeBeau et al. (2000). Although we have no a priori reason to believe that the ionic channels in GnRH neurons in situ are the same as those in GT1 cells, neither do we have detailed measurements of these channels in GnRH neurons, and thus our options are limited. Thus, our initial model (Lee et al., 2010; Duan et al., 2011) used, to a large extent, the same channels and parameters as the earlier models. However, in subsequent work, it has become clear that the full array of channels is not necessary in order to study the mechanisms underlying the interburst interval. Instead, a simpler model can be constructed to do the same job, and it is this simpler model that we mostly discuss here.
4.3.1 The full model
Before we can discuss how our simplified model is constructed, it is first necessary to discuss briefly the construction of the full model (see Figure 4.2 for a schematic diagram). Full details can be found in Lee et al. (2010) and Duan et al. (2011).
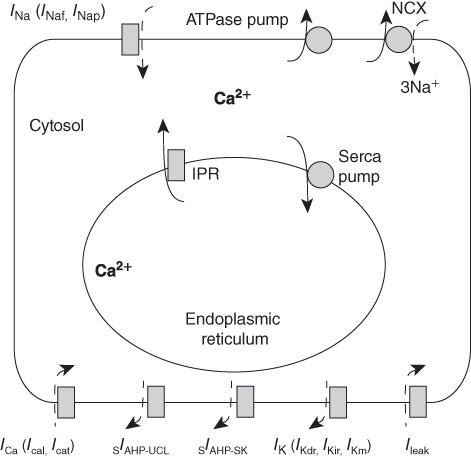
Figure 4.2 Schematic diagram of the model. 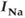 amalgamates two different
amalgamates two different  currents, while
currents, while 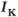 amalgamates three different
amalgamates three different 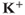 currents. The
currents. The 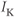 currents combine with the
currents combine with the 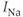 currents to generate oscillatory AC spiking, in the manner of the Hodgkin–Huxley model.
currents to generate oscillatory AC spiking, in the manner of the Hodgkin–Huxley model. 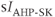 is a
is a 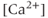 -sensitive and apamin-sensitive
-sensitive and apamin-sensitive 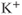 current that is activated when
current that is activated when 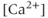 is raised, while
is raised, while 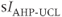 is a
is a 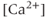 -sensitive and time-dependent
-sensitive and time-dependent 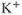 current that is activated by raised
current that is activated by raised 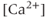 and turns off only gradually, in a
and turns off only gradually, in a 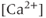 -independent manner. An inward leakage current (
-independent manner. An inward leakage current ( ) is also included. There are five influx or efflux pathways for
) is also included. There are five influx or efflux pathways for 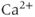 ; the
; the 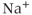 –
–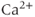 exchanger, the plasma membrane ATPase pump, the
exchanger, the plasma membrane ATPase pump, the 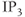 receptor, membrane
receptor, membrane 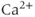 channels and the SERCA pump. The dashed lines represent the direction of net ionic fluxes and the
channels and the SERCA pump. The dashed lines represent the direction of net ionic fluxes and the 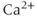 fluxes are denoted by solid lines.
fluxes are denoted by solid lines.
The original GnRH neuron model consists of a membrane potential (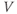 ) submodel and a
) submodel and a 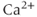 submodel, which simulate the electrical activity and
submodel, which simulate the electrical activity and 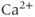 dynamics, respectively. Each submodel can affect the other; the voltage submodel can affect the
dynamics, respectively. Each submodel can affect the other; the voltage submodel can affect the 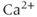 dyamics via the entry of
dyamics via the entry of 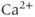 through voltage-gated channels, while the
through voltage-gated channels, while the 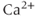 submodel can affect the voltage via
submodel can affect the voltage via 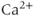 -gated
-gated 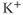 channels.
channels.
Most of the currents included in the 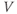 submodel are defined by gating equations, as in the Hodgkin–Huxley model. With one exception, they are standard currents, of the type found in a variety of electrophysiological models. The exception is
submodel are defined by gating equations, as in the Hodgkin–Huxley model. With one exception, they are standard currents, of the type found in a variety of electrophysiological models. The exception is 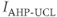 , which is central to our model construction and results, and shall be discussed in more detail later.
, which is central to our model construction and results, and shall be discussed in more detail later.
The equation for 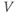 is of the standard form
is of the standard form
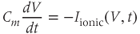
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree



